- Research Article
- Open access
- Published:
Terminal value problem for singular ordinary differential equations: Theoretical analysis and numerical simulations of ground states
Boundary Value Problems volume 2006, Article number: 28719 (2006)
Abstract
A singular boundary value problem (BVP) for a second-order nonlinear differential equation is studied. This BVP is a model in hydrodynamics as well as in nonlinear field theory and especially in the study of the symmetric bubble-type solutions (shell-like theory). The obtained solutions (ground states) can describe the relationship between surface tension, the surface mass density, and the radius of the spherical interfaces between the fluid phases of the same substance. An interval of the parameter, in which there is a strictly increasing and positive solution defined on the half-line, with certain asymptotic behavior is derived. Some numerical results are given to illustrate and verify our results. Furthermore, a full investigation for all other types of solutions is exhibited. The approach is based on the continuum property (connectedness and compactness) of the solutions funnel (Knesser's theorem), combined with the corresponding vector field's ones.
References
Agarwal RP, Kiguradze I: Two-point boundary value problems for higher-order linear differential equations with strong singularities. Boundary Value Problems 2006, 2006: 32 pages.
Baxley JV: Boundary value problems on infinite intervals. In Boundary Value Problems for Functional-Differential Equations. Edited by: Henderson J. World Scientific, New Jersey; 1995:49-62.
Berestycki H, Lions P-L, Peletier LA:An ODE approach to the existence of positive solutions for semilinear problems in
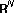 . Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012
. Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012Bonheure D, Gomes JM, Sanchez L: Positive solutions of a second-order singular ordinary differential equation. Nonlinear Analysis 2005,61(8):1383-1399. 10.1016/j.na.2005.02.029
Copel WA: Stability and Asymptotic Behavior of Differential Equations. Heath, Massachusetts; 1965.
Dell'Isola F, Gouin H, Rotoli G: Nucleation of spherical shell-like interfaces by second gradient theory: numerical simulations. European Journal of Mechanics. B. Fluids 1996,15(4):545-568.
Gazzola F, Serrin J, Tang M: Existence of ground states and free boundary problems for quasilinear elliptic operators. Advances in Differential Equations 2000,5(1–3):1-30.
Kuratowski K: Topology II. Academic Press, New York; 1968.
Palamides PK: Singular points of the consequent mapping. Annali di Matematica Pura ed Applicata. Serie Quarta 1981, 129: 383-395 (1982). 10.1007/BF01762151
Palamides PK: Boundary-value problems for shallow elastic membrane caps. IMA Journal of Applied Mathematics 2002,67(3):281-299. 10.1093/imamat/67.3.281
Palamides PK, Galanis GN: Positive, unbounded and monotone solutions of the singular second Painlevé equation on the half-line. Nonlinear Analysis 2004,57(3):401-419. 10.1016/j.na.2004.02.021
Rocard Y: Thermodynamique. Masson, Paris; 1967. chapter 5
Walter W: Ordinary Differential Equations, Graduate Texts in Mathematics. Volume 182. Springer, New York; 1998:xii+380.
Wasov W: Asymptotic Expressions for Ordinary Differential Equations. John Wiley & Sons, New York; 1965.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Palamides, A.P., Yannopoulos, T.G. Terminal value problem for singular ordinary differential equations: Theoretical analysis and numerical simulations of ground states. Bound Value Probl 2006, 28719 (2006). https://doi.org/10.1155/BVP/2006/28719
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/BVP/2006/28719
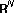 . Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012
. Indiana University Mathematics Journal 1981,30(1):141-157. 10.1512/iumj.1981.30.30012