- Research Article
- Open access
- Published:
Eigenvalue Problems and Bifurcation of Nonhomogeneous Semilinear Elliptic Equations in Exterior Strip Domains
Boundary Value Problems volume 2007, Article number: 014731 (2006)
Abstract
We consider the following eigenvalue problems: in
in in
in where
where ,
, ,
, is a smooth bounded domain,
is a smooth bounded domain, ,
, is a smooth bounded domain in
is a smooth bounded domain in such that
such that . Under some suitable conditions on
. Under some suitable conditions on and
and , we show that there exists a positive constant
, we show that there exists a positive constant such that the above-mentioned problems have at least two solutions if
such that the above-mentioned problems have at least two solutions if , a unique positive solution if
, a unique positive solution if , and no solution if
, and no solution if . We also obtain some bifurcation results of the solutions at
. We also obtain some bifurcation results of the solutions at .
.
References
Cao DM: Eigenvalue problems and bifurcation of semilinear elliptic equation in
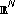 . Nonlinear Analysis. Theory, Methods & Applications 1995,24(4):529–554. 10.1016/0362-546X(94)E0071-N
. Nonlinear Analysis. Theory, Methods & Applications 1995,24(4):529–554. 10.1016/0362-546X(94)E0071-NZhu XP: A perturbation result on positive entire solutions of a semilinear elliptic equation. Journal of Differential Equations 1991,92(2):163–178. 10.1016/0022-0396(91)90045-B
Cao DM, Zhou H-S: Multiple positive solutions of nonhomogeneous semilinear elliptic equations in
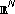 . Proceedings of the Royal Society of Edinburgh. Section A 1996,126(2):443–463. 10.1017/S0308210500022836
. Proceedings of the Royal Society of Edinburgh. Section A 1996,126(2):443–463. 10.1017/S0308210500022836Zhu XP, Zhou HS: Existence of multiple positive solutions of inhomogeneous semilinear elliptic problems in unbounded domains. Proceedings of the Royal Society of Edinburgh. Section A 1990,115(3–4):301–318. 10.1017/S0308210500020667
Esteban MJ: Nonlinear elliptic problems in strip-like domains: symmetry of positive vortex rings. Nonlinear Analysis. Theory, Methods & Applications 1983,7(4):365–379. 10.1016/0362-546X(83)90090-1
Lions P-L: The concentration-compactness principle in the calculus of variations. The locally compact case. I. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1984,1(2):109–145.
Lions P-L: The concentration-compactness principle in the calculus of variations. The locally compact case. II. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1984,1(4):223–283.
Bahri A, Lions P-L: On the existence of a positive solution of semilinear elliptic equations in unbounded domains. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1997,14(3):365–413.
Lions P-L: On positive solutions of semilinear elliptic equations in unbounded domains. In Nonlinear Diffusion Equations and Their Equilibrium States, II (Berkeley, CA, 1986), Math. Sci. Res. Inst. Publ.. Volume 13. Edited by: Ni W-M, Peletier LA, Serrin J. Springer, New York, NY, USA; 1988:85–122.
Hsu T-S: Exactly two positive solutions of nonhomogeneous semilinear elliptic equations in unbounded cylinder domains. Dynamics of Continuous, Discrete & Impulsive Systems. Series A. Mathematical Analysis 2005,12(5):685–705.
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Fundamental Principles of Mathematical Sciences. Volume 224. 2nd edition. Springer, Berlin, Germany; 1983.
Adams RA: Sobolev Spaces, Pure and Applied Mathematics. Volume 65. Academic Press, New York, NY, USA; 1975.
Hsu T-S: Multiple solutions for semilinear elliptic equations in unbounded cylinder domains. Proceedings of the Royal Society of Edinburgh. Section A 2004,134(4):719–731. 10.1017/S0308210500003449
Ekeland I: Nonconvex minimization problems. Bulletin of the American Mathematical Society 1979,1(3):443–474. 10.1090/S0273-0979-1979-14595-6
Graham-Eagle J: Monotone methods for semilinear elliptic equations in unbounded domains. Journal of Mathematical Analysis and Applications 1989,137(1):122–131. 10.1016/0022-247X(89)90276-X
Ambrosetti A, Rabinowitz PH: Dual variational methods in critical point theory and applications. Journal of Functional Analysis 1973,14(4):349–381. 10.1016/0022-1236(73)90051-7
Crandall MG, Rabinowitz PH: Bifurcation, perturbation of simple eigenvalues and linearized stability. Archive for Rational Mechanics and Analysis 1973,52(2):161–180.
Korman P, Li Y, Ouyang T: Exact multiplicity results for boundary value problems with nonlinearities generalising cubic. Proceedings of the Royal Society of Edinburgh. Section A 1996,126(3):599–616. 10.1017/S0308210500022927
Lien WC, Tzeng SY, Wang HC: Existence of solutions of semilinear elliptic problems on unbounded domains. Differential and Integral Equations 1993,6(6):1281–1298.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hsu, TS. Eigenvalue Problems and Bifurcation of Nonhomogeneous Semilinear Elliptic Equations in Exterior Strip Domains. Bound Value Probl 2007, 014731 (2006). https://doi.org/10.1155/2007/14731
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/14731
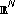 . Nonlinear Analysis. Theory, Methods & Applications 1995,24(4):529–554. 10.1016/0362-546X(94)E0071-N
. Nonlinear Analysis. Theory, Methods & Applications 1995,24(4):529–554. 10.1016/0362-546X(94)E0071-N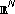 . Proceedings of the Royal Society of Edinburgh. Section A 1996,126(2):443–463. 10.1017/S0308210500022836
. Proceedings of the Royal Society of Edinburgh. Section A 1996,126(2):443–463. 10.1017/S0308210500022836