- Research Article
- Open access
- Published:
Reverse Smoothing Effects, Fine Asymptotics, and Harnack Inequalities for Fast Diffusion Equations
Boundary Value Problems volume 2007, Article number: 021425 (2006)
Abstract
We investigate local and global properties of positive solutions to the fast diffusion equation in the good exponent range
in the good exponent range , corresponding to general nonnegative initial data. For the Cauchy problem posed in the whole Euclidean space
, corresponding to general nonnegative initial data. For the Cauchy problem posed in the whole Euclidean space , we prove sharp local positivity estimates (weak Harnack inequalities) and elliptic Harnack inequalities; also a slight improvement of the intrinsic Harnack inequality is given. We use them to derive sharp global positivity estimates and a global Harnack principle. Consequences of these latter estimates in terms of fine asymptotics are shown. For the mixed initial and boundary value problem posed in a bounded domain of
, we prove sharp local positivity estimates (weak Harnack inequalities) and elliptic Harnack inequalities; also a slight improvement of the intrinsic Harnack inequality is given. We use them to derive sharp global positivity estimates and a global Harnack principle. Consequences of these latter estimates in terms of fine asymptotics are shown. For the mixed initial and boundary value problem posed in a bounded domain of with homogeneous Dirichlet condition, we prove weak, intrinsic, and elliptic Harnack inequalities for intermediate times. We also prove elliptic Harnack inequalities near the extinction time, as a consequence of the study of the fine asymptotic behavior near the finite extinction time.
with homogeneous Dirichlet condition, we prove weak, intrinsic, and elliptic Harnack inequalities for intermediate times. We also prove elliptic Harnack inequalities near the extinction time, as a consequence of the study of the fine asymptotic behavior near the finite extinction time.
References
Vazquez JL: Asymptotic beahviour for the porous medium equation posed in the whole space. Journal of Evolution Equations 2003,3(1):67–118. 10.1007/s000280300004
Vazquez JL: The Dirichlet problem for the porous medium equation in bounded domains. Asymptotic behavior. Monatshefte für Mathematik 2004,142(1–2):81–111. 10.1007/s00605-004-0237-4
Vazquez JL: Smoothing and Decay Estimates for Nonlinear Diffusion Equations. Equations of Porous Medium Type, Lecture Notes. Oxford University Press, New York; 2006.
Bonforte M, Vazquez JL: Fine asymptotics and elliptic Harnack inequalities near the extinction time for fast diffusion equation. preprint, 2006
Bonforte M, Vazquez JL: Global positivity estimates and Harnack inequalities for the fast diffusion equation. preprint, 2005
Chen YZ, DiBenedetto E: On the local behavior of solutions of singular parabolic equations. Archive for Rational Mechanics and Analysis 1988,103(4):319–345.
DiBenedetto E, Kwong YC, Vespri V: Local space-analyticity of solutions of certain singular parabolic equations. Indiana University Mathematics Journal 1991,40(2):741–765. 10.1512/iumj.1991.40.40033
Aronson DG, Caffarelli LA: The initial trace of a solution of the porous medium equation. Transactions of the American Mathematical Society 1983,280(1):351–366. 10.1090/S0002-9947-1983-0712265-1
Herrero MA, Pierre M: The Cauchy problem for
 when
when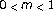 . Transactions of the American Mathematical Society 1985,291(1):145–158.
. Transactions of the American Mathematical Society 1985,291(1):145–158.Lee K-A, Vazquez JL: Geometrical properties of solutions of the porous medium equation for large times. Indiana University Mathematics Journal 2003,52(4):991–1016.
Carrillo JA, Vazquez JL: Fine asymptotics for fast diffusion equations. Communications in Partial Differential Equations 2003,28(5–6):1023–1056. 10.1081/PDE-120021185
Bénilan P, Crandall MG: Regularizing effects of homogeneous evolution equations. In Contributions to Analysis and Geometry (Baltimore, Md., 1980), Suppl. Am. J. Math.. Johns Hopkins University Press, Maryland; 1981:23–39.
Berryman JG, Holland CJ: Stability of the separable solution for fast diffusion. Archive for Rational Mechanics and Analysis 1980,74(4):379–388.
Adimurthi , Yadava SL: An elementary proof of the uniqueness of positive radial solutions of a quasilinear Dirichlet problem. Archive for Rational Mechanics and Analysis 1994,127(3):219–229. 10.1007/BF00381159
Ni W-M, Nussbaum RD: Uniqueness and nonuniqueness for positive radial solutions of
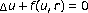 . Communications on Pure and Applied Mathematics 1985,38(1):67–108. 10.1002/cpa.3160380105
. Communications on Pure and Applied Mathematics 1985,38(1):67–108. 10.1002/cpa.3160380105Budd C, Norbury J: Semilinear elliptic equations and supercritical growth. Journal of Differential Equations 1987,68(2):169–197. 10.1016/0022-0396(87)90190-2
Galaktionov VA, Vazquez JL: A Stability Technique for Evolution Partial Differential Equations. A Dynamical System Approach, Progress in Nonlinear Differential Equations and Their Applications. Volume 56. Birkhäuser Boston, Massachusetts; 2004:xxii+377.
Hale JK: Asymptotic Behavior of Dissipative Systems, Mathematical Surveys and Monographs. Volume 25. American Mathematical Society, Rhode Island; 1988:x+198.
DiBenedetto E, Kwong YC: Harnack estimates and extinction profile for weak solutions of certain singular parabolic equations. Transactions of the American Mathematical Society 1992,330(2):783–811. 10.2307/2153935
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Grundlehren der mathematischen Wissenschaften. Volume 224. Springer, Berlin; 1977:x+401.
Aronson DG, Peletier LA: Large time behaviour of solutions of the porous medium equation in bounded domains. Journal of Differential Equations 1981,39(3):378–412. 10.1016/0022-0396(81)90065-6
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bonforte, M., Vazquez, J.L. Reverse Smoothing Effects, Fine Asymptotics, and Harnack Inequalities for Fast Diffusion Equations. Bound Value Probl 2007, 021425 (2006). https://doi.org/10.1155/2007/21425
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/21425
 when
when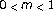 . Transactions of the American Mathematical Society 1985,291(1):145–158.
. Transactions of the American Mathematical Society 1985,291(1):145–158.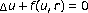 . Communications on Pure and Applied Mathematics 1985,38(1):67–108. 10.1002/cpa.3160380105
. Communications on Pure and Applied Mathematics 1985,38(1):67–108. 10.1002/cpa.3160380105