- Research Article
- Open access
- Published:
The Monotone Iterative Technique for Three-Point Second-Order Integrodifferential Boundary Value Problems with -Laplacian
-Laplacian
Boundary Value Problems volume 2007, Article number: 057481 (2007)
Abstract
A monotone iterative technique is applied to prove the existence of the extremal positive pseudosymmetric solutions for a three-point second-order -Laplacian integrodifferential boundary value problem.
-Laplacian integrodifferential boundary value problem.
References
Il'in VA, Moiseev EI: Nonlocal boundary value problem of the first kind for a Sturm-Liouville operator in its differential and finite difference aspects. Differential Equations 1987,23(7):803-811.
Il'in VA, Moiseev EI: Nonlocal boundary-value problem of the secod kind for a Sturm-Liouville operator. Differential Equations 1987,23(8):979-987.
Gupta CP: Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equation. Journal of Mathematical Analysis and Applications 1992,168(2):540-551. 10.1016/0022-247X(92)90179-H
Lian WC, Wong FH, Yeh CC: On the existence of positive solutions of nonlinear second order differential equations. Proceedings of the American Mathematical Society 1996,124(4):1117-1126. 10.1090/S0002-9939-96-03403-X
Ma R: Positive solutions of a nonlinear three-point boundary-value problem. Electronic Journal of Differential Equations 1999, (34):1-8.
Ma R, Castaneda N:Existence of solutions of nonlinear
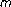 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320Coppel WA: Disconjugacy, Lecture Notes in Mathematics. Volume 220. Springer, New York, NY, USA; 1971:iv+148.
Eloe PW, Ahmad B:Positive solutions of a nonlinear
 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009Wang J-Y, Zheng D-W:On the existence of positive solutions to a three-point boundary value problem for the one-dimensional
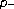 Laplacian. Zeitschrift für Angewandte Mathematik und Mechanik 1997,77(6):477-479. 10.1002/zamm.19970770618
Laplacian. Zeitschrift für Angewandte Mathematik und Mechanik 1997,77(6):477-479. 10.1002/zamm.19970770618He X, Ge W:A remark on some three-point boundary value problems for the one-dimensional
 Laplacian. Zeitschrift für Angewandte Mathematik und Mechanik 2002,82(10):728-731. 10.1002/1521-4001(200210)82:10<728::AID-ZAMM728>3.0.CO;2-R
Laplacian. Zeitschrift für Angewandte Mathematik und Mechanik 2002,82(10):728-731. 10.1002/1521-4001(200210)82:10<728::AID-ZAMM728>3.0.CO;2-RAvery R, Henderson J:Existence of three positive pseudo-symmetric solutions for a one-dimensional
 Laplacian. Journal of Mathematical Analysis and Applications 2003,277(2):395-404. 10.1016/S0022-247X(02)00308-6
Laplacian. Journal of Mathematical Analysis and Applications 2003,277(2):395-404. 10.1016/S0022-247X(02)00308-6Guo Y, Ge W:Three positive solutions for the one-dimensional
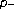 Laplacian. Journal of Mathematical Analysis and Applications 2003,286(2):491-508. 10.1016/S0022-247X(03)00476-1
Laplacian. Journal of Mathematical Analysis and Applications 2003,286(2):491-508. 10.1016/S0022-247X(03)00476-1He X, Ge W:Twin positive solutions for the one-dimensional
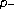 Laplacian boundary value problems. Nonlinear Analysis 2004,56(7):975-984. 10.1016/j.na.2003.07.022
Laplacian boundary value problems. Nonlinear Analysis 2004,56(7):975-984. 10.1016/j.na.2003.07.022Li J, Shen J:Existence of three positive solutions for boundary value problems with
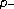 Laplacian. Journal of Mathematical Analysis and Applications 2005,311(2):457-465. 10.1016/j.jmaa.2005.02.054
Laplacian. Journal of Mathematical Analysis and Applications 2005,311(2):457-465. 10.1016/j.jmaa.2005.02.054Wang Z, Zhang J:Positive solutions for one-dimensional
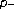 Laplacian boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2006,314(2):618-630. 10.1016/j.jmaa.2005.04.012
Laplacian boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2006,314(2):618-630. 10.1016/j.jmaa.2005.04.012Wang Y, Hou C:Existence of multiple positive solutions for one-dimensional
 Laplacian. Journal of Mathematical Analysis and Applications 2006,315(1):144-153. 10.1016/j.jmaa.2005.09.085
Laplacian. Journal of Mathematical Analysis and Applications 2006,315(1):144-153. 10.1016/j.jmaa.2005.09.085Ma D-X, Du Z-J, Ge W-G:Existence and iteration of monotone positive solutions for multipoint boundary value problem with
 Laplacian operator. Computers & Mathematics with Applications 2005,50(5-6):729-739. 10.1016/j.camwa.2005.04.016
Laplacian operator. Computers & Mathematics with Applications 2005,50(5-6):729-739. 10.1016/j.camwa.2005.04.016Ma D-X, Ge W:Existence and iteration of positive pseudo-symmetric solutions for a three-point second order
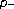 Laplacian BVP. Applied Mathematics Letters 2007.
Laplacian BVP. Applied Mathematics Letters 2007.Amann H: Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Review 1976,18(4):620-709. 10.1137/1018114
Ladde GS, Lakshmikantham V, Vatsala AS: Monotone Iterative Techniques for Nonlinear Differential Equations, Monographs, Advanced Texts and Surveys in Pure and Applied Mathematics. Volume 27. Pitman, Boston, Mass, USA; 1985:x+236.
Nieto JJ, Jiang Y, Jurang Y: Monotone iterative method for functional-differential equations. Nonlinear Analysis 1998,32(6):741-747. 10.1016/S0362-546X(97)00524-5
Vatsala AS, Yang J: Monotone iterative technique for semilinear elliptic systems. Boundary Value Problems 2005,2005(2):93-106. 10.1155/BVP.2005.93
Drici Z, McRae FA, Vasundhara Devi J: Monotone iterative technique for periodic boundary value problems with causal operators. Nonlinear Analysis 2006,64(6):1271-1277. 10.1016/j.na.2005.06.033
West IH, Vatsala AS: Generalized monotone iterative method for initial value problems. Applied Mathematics Letters 2004,17(11):1231-1237. 10.1016/j.aml.2004.03.003
Jiang D, Nieto JJ, Zuo W: On monotone method for first and second order periodic boundary value problems and periodic solutions of functional differential equations. Journal of Mathematical Analysis and Applications 2004,289(2):691-699. 10.1016/j.jmaa.2003.09.020
Nieto JJ, Rodríguez-López R: Monotone method for first-order functional differential equations. Computers & Mathematics with Applications 2006,52(3-4):471-484. 10.1016/j.camwa.2006.01.012
Ahmad B, Sivasundaram S: The monotone iterative technique for impulsive hybrid set valued integro-differential equations. Nonlinear Analysis 2006,65(12):2260-2276. 10.1016/j.na.2006.01.033
Nieto JJ: An abstract monotone iterative technique. Nonlinear Analysis 1997,28(12):1923-1933. 10.1016/S0362-546X(97)89710-6
Liz E, Nieto JJ: An abstract monotone iterative method and applications. Dynamic Systems and Applications 1998,7(3):365-375.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ahmad, B., Nieto, J.J. The Monotone Iterative Technique for Three-Point Second-Order Integrodifferential Boundary Value Problems with -Laplacian.
Bound Value Probl 2007, 057481 (2007). https://doi.org/10.1155/2007/57481
-Laplacian.
Bound Value Probl 2007, 057481 (2007). https://doi.org/10.1155/2007/57481
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/57481
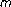 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009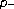 Laplacian. Zeitschrift für Angewandte Mathematik und Mechanik 1997,77(6):477-479. 10.1002/zamm.19970770618
Laplacian. Zeitschrift für Angewandte Mathematik und Mechanik 1997,77(6):477-479. 10.1002/zamm.19970770618 Laplacian. Zeitschrift für Angewandte Mathematik und Mechanik 2002,82(10):728-731. 10.1002/1521-4001(200210)82:10<728::AID-ZAMM728>3.0.CO;2-R
Laplacian. Zeitschrift für Angewandte Mathematik und Mechanik 2002,82(10):728-731. 10.1002/1521-4001(200210)82:10<728::AID-ZAMM728>3.0.CO;2-R Laplacian. Journal of Mathematical Analysis and Applications 2003,277(2):395-404. 10.1016/S0022-247X(02)00308-6
Laplacian. Journal of Mathematical Analysis and Applications 2003,277(2):395-404. 10.1016/S0022-247X(02)00308-6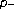 Laplacian. Journal of Mathematical Analysis and Applications 2003,286(2):491-508. 10.1016/S0022-247X(03)00476-1
Laplacian. Journal of Mathematical Analysis and Applications 2003,286(2):491-508. 10.1016/S0022-247X(03)00476-1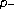 Laplacian boundary value problems. Nonlinear Analysis 2004,56(7):975-984. 10.1016/j.na.2003.07.022
Laplacian boundary value problems. Nonlinear Analysis 2004,56(7):975-984. 10.1016/j.na.2003.07.022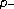 Laplacian. Journal of Mathematical Analysis and Applications 2005,311(2):457-465. 10.1016/j.jmaa.2005.02.054
Laplacian. Journal of Mathematical Analysis and Applications 2005,311(2):457-465. 10.1016/j.jmaa.2005.02.054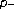 Laplacian boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2006,314(2):618-630. 10.1016/j.jmaa.2005.04.012
Laplacian boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2006,314(2):618-630. 10.1016/j.jmaa.2005.04.012 Laplacian. Journal of Mathematical Analysis and Applications 2006,315(1):144-153. 10.1016/j.jmaa.2005.09.085
Laplacian. Journal of Mathematical Analysis and Applications 2006,315(1):144-153. 10.1016/j.jmaa.2005.09.085 Laplacian operator. Computers & Mathematics with Applications 2005,50(5-6):729-739. 10.1016/j.camwa.2005.04.016
Laplacian operator. Computers & Mathematics with Applications 2005,50(5-6):729-739. 10.1016/j.camwa.2005.04.016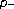 Laplacian BVP. Applied Mathematics Letters 2007.
Laplacian BVP. Applied Mathematics Letters 2007.