- Research Article
- Open access
- Published:
Harnack Inequalities: An Introduction
Boundary Value Problems volume 2007, Article number: 081415 (2007)
Abstract
The aim of this article is to give an introduction to certain inequalities named after Carl Gustav Axel von Harnack. These inequalities were originally defined for harmonic functions in the plane and much later became an important tool in the general theory of harmonic functions and partial differential equations. We restrict ourselves mainly to the analytic perspective but comment on the geometric and probabilistic significance of Harnack inequalities. Our focus is on classical results rather than latest developments. We give many references to this topic but emphasize that neither the mathematical story of Harnack inequalities nor the list of references given here is complete.
[123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128]
References
Voss A: Zur Erinnerung an Axel Harnack. Mathematische Annalen 1888,32(2):161-174. 10.1007/BF01444065
Axel Harnack C-G: Die Grundlagen der Theorie des logarithmischen Potentiales und der eindeutigen Potentialfunktion in der Ebene. Teubner, Leipzig, Germany; 1887. see also The Cornell Library Historical Mathematics Monographs
Poincaré H: Sur les Equations aux Derivees Partielles de la Physique Mathematique. American Journal of Mathematics 1890,12(3):211-294. 10.2307/2369620
Lichtenstein L: Beiträge zur Theorie der linearen partiellen Differentialgleichungen zweiter Ordnung vom elliptischen Typus. Unendliche Folgen positiver Lösungen. Rendiconti del Circolo Matematico di Palermo 1912, 33: 201-211. 10.1007/BF03015300
Lichtenstein L: Randwertaufgaben der Theorie der linearen partiellen Differentialgleichungen zweiter Ordnung vom elliptischen Typus. I. Journal für die Reine und Angewandte Mathematik 1913, 142: 1-40.
Feller W: Über die Lösungen der linearen partiellen Differentialgleichungen zweiter Ordnung vom elliptischen Typus. Mathematische Annalen 1930,102(1):633-649. 10.1007/BF01782367
Serrin J: On the Harnack inequality for linear elliptic equations. Journal d'Analyse Mathématique 1955/1956, 4: 292-308.
Bers L, Nirenberg L: On linear and non-linear elliptic boundary value problems in the plane. In Convegno Internazionale sulle Equazioni Lineari alle Derivate Parziali, Trieste, 1954. Edizioni Cremonese, Rome, Italy; 1955:141-167.
Lichtenstein L: Neuere Entwicklung der Potentialtheorie. Konforme Abbildung. Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen 1918, 2, T.3, H.1: 177-377.
Kellogg OD: Foundations of Potential Theorie, Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen Bd. 31. Springer, Berlin, Germany; 1929.
Riesz M: Intégrales de Riemann-Liouville et potentiels. Acta Scientiarum Mathematicarum (Szeged) 1938, 9: 1-42.
Landkof NS: Foundations of Modern Potential Theory, Die Grundlehren der mathematischen Wissenschaften, Band 180. Springer, New York, NY, USA; 1972:x+424.
Pini B: Sulla soluzione generalizzata di Wiener per il primo problema di valori al contorno nel caso parabolico. Rendiconti del Seminario Matematico della Università di Padova 1954, 23: 422-434.
Hadamard J: Extension à l'équation de la chaleur d'un théorème de A. Harnack. Rendiconti del Circolo Matematico di Palermo. Serie II 1954, 3: 337-346 (1955). 10.1007/BF02849264
Moser J: A Harnack inequality for parabolic differential equations. Communications on Pure and Applied Mathematics 1964, 17: 101-134. 10.1002/cpa.3160170106
Auchmuty G, Bao D: Harnack-type inequalities for evolution equations. Proceedings of the American Mathematical Society 1994,122(1):117-129. 10.1090/S0002-9939-1994-1219716-X
Li P, Yau Sh-T: On the parabolic kernel of the Schrödinger operator. Acta Mathematica 1986,156(3-4):153-201.
Moser J: On Harnack's theorem for elliptic differential equations. Communications on Pure and Applied Mathematics 1961, 14: 577-591. 10.1002/cpa.3160140329
De Giorgi E: Sulla differenziabilità e l'analiticità delle estremali degli integrali multipli regolari. Memorie dell'Accademia delle Scienze di Torino. Classe di Scienze Fisiche, Matematiche e Naturali. Serie III 1957, 3: 25-43.
John F, Nirenberg L: On functions of bounded mean oscillation. Communications on Pure and Applied Mathematics 1961, 14: 415-426. 10.1002/cpa.3160140317
Bombieri E, Giusti E: Harnack's inequality for elliptic differential equations on minimal surfaces. Inventiones Mathematicae 1972,15(1):24-46. 10.1007/BF01418640
Han Q, Lin F: Elliptic Partial Differential Equations, Courant Lecture Notes in Mathematics. Volume 1. New York University Courant Institute of Mathematical Sciences, New York, NY, USA; 1997:x+144.
Grüter M, Widman Kj-O: The Green function for uniformly elliptic equations. Manuscripta Mathematica 1982,37(3):303-342. 10.1007/BF01166225
Bensoussan A, Frehse J: Regularity Results for Nonlinear Elliptic Systems and Applications, Applied Mathematical Sciences. Volume 151. Springer, Berlin, Germany; 2002:xii+441.
Nash J: Continuity of solutions of parabolic and elliptic equations. American Journal of Mathematics 1958,80(4):931-954. 10.2307/2372841
DiBenedetto E, Trudinger NS: Harnack inequalities for quasiminima of variational integrals. Annales de l'Institut Henri Poincaré. Analyse Non Linéaire 1984,1(4):295-308.
DiBenedetto E: Harnack estimates in certain function classes. Atti del Seminario Matematico e Fisico dell'Università di Modena 1989,37(1):173-182.
Serrin J: Local behavior of solutions of quasi-linear equations. Acta Mathematica 1964,111(1):247-302. 10.1007/BF02391014
Trudinger NS: On Harnack type inequalities and their application to quasilinear elliptic equations. Communications on Pure and Applied Mathematics 1967, 20: 721-747. 10.1002/cpa.3160200406
Trudinger NS: Harnack inequalities for nonuniformly elliptic divergence structure equations. Inventiones Mathematicae 1981,64(3):517-531. 10.1007/BF01389280
Ladyzhenskaya OA, Ural'tseva NN: Linear and Quasilinear Elliptic Equations. Academic Press, New York, NY, USA; 1968:xviii+495.
Moser J: Correction to: "A Harnack inequality for parabolic differential equations". Communications on Pure and Applied Mathematics 1967, 20: 231-236. 10.1002/cpa.3160200107
Moser J: On a pointwise estimate for parabolic differential equations. Communications on Pure and Applied Mathematics 1971, 24: 727-740. 10.1002/cpa.3160240507
Fabes EB, Garofalo N: Parabolic B.M.O. and Harnack's inequality. Proceedings of the American Mathematical Society 1985,95(1):63-69.
Ferretti E, Safonov MV: Growth theorems and Harnack inequality for second order parabolic equations. In Harmonic Analysis and Boundary Value Problems (Fayetteville, AR, 2000), Contemp. Math.. Volume 277. American Mathematical Society, Providence, RI, USA; 2001:87-112.
Safonov MV: Mean value theorems and Harnack inequalities for second-order parabolic equations. In Nonlinear Problems in Mathematical Physics and Related Topics, II, Int. Math. Ser. (N. Y.). Volume 2. Kluwer/Plenum, New York, NY, USA; 2002:329-352. 10.1007/978-1-4615-0701-7_18
Aronson DG: Bounds for the fundamental solution of a parabolic equation. Bulletin of the American Mathematical Society 1967, 73: 890-896. 10.1090/S0002-9904-1967-11830-5
Fabes EB, Stroock DW: A new proof of Moser's parabolic Harnack inequality using the old ideas of Nash. Archive for Rational Mechanics and Analysis 1986,96(4):327-338.
Fabes EB, Stroock DW:The
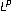 -integrability of Green's functions and fundamental solutions for elliptic and parabolic equations. Duke Mathematical Journal 1984,51(4):997-1016. 10.1215/S0012-7094-84-05145-7
-integrability of Green's functions and fundamental solutions for elliptic and parabolic equations. Duke Mathematical Journal 1984,51(4):997-1016. 10.1215/S0012-7094-84-05145-7Aronson DG, Serrin J: Local behavior of solutions of quasilinear parabolic equations. Archive for Rational Mechanics and Analysis 1967, 25: 81-122. 10.1007/BF00281291
Ivanov AV: The Harnack inequality for generalized solutions of second order quasilinear parabolic equations. Trudy Matematicheskogo Instituta imeni V. A. Steklova 1967, 102: 51-84.
Trudinger NS: Pointwise estimates and quasilinear parabolic equations. Communications on Pure and Applied Mathematics 1968, 21: 205-226. 10.1002/cpa.3160210302
DiBenedetto E: Degenerate Parabolic Equations, Universitext. Springer, New York, NY, USA; 1993:xvi+387.
Ivanov AV: Second-order quasilinear degenerate and nonuniformly elliptic and parabolic equations. Trudy Matematicheskogo Instituta imeni V. A. Steklova 1982, 160: 285.
Porper FO, Èĭdel'man SD: Two-sided estimates of the fundamental solutions of second-order parabolic equations and some applications of them. Uspekhi Matematicheskikh Nauk 1984,39(3(237)):107-156.
Ladyzhenskaya OA, Solonnikov VA, Ural'tseva NN: Linear and Quasi-Linear Equations of Parabolic Type, Translations of Mathematical Monographs. Volume 23. American Mathematical Society, Providence, RI, USA; 1968.
Kruzhkov SN: A priori estimation of solutions of linear parabolic equations and of boundary value problems for a certain class of quasilinear parabolic equations. Soviet Mathematics. Doklady 1961, 2: 764-767.
Kruzhkov SN: A priori estimates and certain properties of the solutions of elliptic and parabolic equations. American Mathematical Society Translations. Series 2 1968, 68: 169-220.
Kružkov SN: Results concerning the nature of the continuity of solutions of parabolic equations and some of their applications. Mathematical Notes 1969, 6: 517-523. 10.1007/BF01450257
Chiarenza FM, Serapioni RP: A Harnack inequality for degenerate parabolic equations. Communications in Partial Differential Equations 1984,9(8):719-749. 10.1080/03605308408820346
DiBenedetto E: Intrinsic Harnack type inequalities for solutions of certain degenerate parabolic equations. Archive for Rational Mechanics and Analysis 1988,100(2):129-147. 10.1007/BF00282201
DiBenedetto E, Urbano JM, Vespri V: Current issues on singular and degenerate evolution equations. In Evolutionary Equations. Vol. I, Handb. Differ. Equ.. North-Holland, Amsterdam, The Netherlands; 2004:169-286.
DiBenedetto E, Gianazza U, Vespri V: Intrinsic Harnack estimates for nonnegative local solutions of degenerate parabolic equatoins. Electronic Research Announcements of the American Mathematical Society 2006, 12: 95-99. 10.1090/S1079-6762-06-00166-1
Gianazza U, Vespri V: A Harnack inequality for a degenerate parabolic equation. Journal of Evolution Equations 2006,6(2):247-267. 10.1007/s00028-006-0242-2
Gianazza U, Vespri V:Parabolic De Giorgi classes of order
 and the Harnack inequality. Calculus of Variations and Partial Differential Equations 2006,26(3):379-399. 10.1007/s00526-006-0022-4
and the Harnack inequality. Calculus of Variations and Partial Differential Equations 2006,26(3):379-399. 10.1007/s00526-006-0022-4Kruzhkov SN: Certain properties of solutions to elliptic equations. Soviet Mathematics. Doklady 1963, 4: 686-690.
Murthy MKV, Stampacchia G: Boundary value problems for some degenerate-elliptic operators. Annali di Matematica Pura ed Applicata 1968,80(1):1-122. 10.1007/BF02413623
Murthy MKV, Stampacchia G: Errata corrige: "Boundary value problems for some degenerate-elliptic operators". Annali di Matematica Pura ed Applicata 1971,90(1):413-414. 10.1007/BF02415055
Edmunds DE, Peletier LA: A Harnack inequality for weak solutions of degenerate quasilinear elliptic equations. Journal of the London Mathematical Society. Second Series 1972, 5: 21-31. 10.1112/jlms/s2-5.1.21
Fabes EB, Kenig CE, Serapioni RP: The local regularity of solutions of degenerate elliptic equations. Communications in Partial Differential Equations 1982,7(1):77-116. 10.1080/03605308208820218
Trudinger NS: On the regularity of generalized solutions of linear, non-uniformly elliptic equations. Archive for Rational Mechanics and Analysis 1971,42(1):50-62.
Franchi B, Serapioni R, Serra Cassano F: Irregular solutions of linear degenerate elliptic equations. Potential Analysis 1998,9(3):201-216. 10.1023/A:1008684127989
Chiarenza F, Serapioni R: Pointwise estimates for degenerate parabolic equations. Applicable Analysis 1987,23(4):287-299. 10.1080/00036818708839648
Kružkov SN, Kolodīĭ ĪM: A priori estimates and Harnack's inequality for generalized solutions of degenerate quasilinear parabolic equations. Sibirskiĭ Matematičeskiĭ Žurnal 1977,18(3):608-628, 718.
Chanillo S, Wheeden RL: Harnack's inequality and mean-value inequalities for solutions of degenerate elliptic equations. Communications in Partial Differential Equations 1986,11(10):1111-1134. 10.1080/03605308608820458
Chanillo S, Wheeden RL: Existence and estimates of Green's function for degenerate elliptic equations. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1988,15(2):309-340 (1989).
Chiarenza F, Rustichini A, Serapioni R: De Giorgi-Moser theorem for a class of degenerate non-uniformly elliptic equations. Communications in Partial Differential Equations 1989,14(5):635-662. 10.1080/03605308908820623
Salinas O: Harnack inequality and Green function for a certain class of degenerate elliptic differential operators. Revista Matemática Iberoamericana 1991,7(3):313-349.
Franchi B, Gutiérrez CrE, Wheeden RL: Weighted Sobolev-Poincaré inequalities for Grushin type operators. Communications in Partial Differential Equations 1994,19(3-4):523-604. 10.1080/03605309408821025
De Cicco V, Vivaldi MA: Harnack inequalities for Fuchsian type weighted elliptic equations. Communications in Partial Differential Equations 1996,21(9-10):1321-1347. 10.1080/03605309608821229
Gutiérrez CrE, Lanconelli E:Maximum principle, nonhomogeneous Harnack inequality, and Liouville theorems for
 -elliptic operators. Communications in Partial Differential Equations 2003,28(11-12):1833-1862. 10.1081/PDE-120025487
-elliptic operators. Communications in Partial Differential Equations 2003,28(11-12):1833-1862. 10.1081/PDE-120025487Mohammed A: Harnack's inequality for solutions of some degenerate elliptic equations. Revista Matemática Iberoamericana 2002,18(2):325-354.
Trudinger NS, Wang X-J: On the weak continuity of elliptic operators and applications to potential theory. American Journal of Mathematics 2002,124(2):369-410. 10.1353/ajm.2002.0012
Zamboni P: Hölder continuity for solutions of linear degenerate elliptic equations under minimal assumptions. Journal of Differential Equations 2002,182(1):121-140. 10.1006/jdeq.2001.4094
Fernandes JD, Groisman J, Melo ST: Harnack inequality for a class of degenerate elliptic operators. Zeitschrift für Analysis und ihre Anwendungen 2003,22(1):129-146.
Ferrari F:Harnack inequality for two-weight subelliptic
 -Laplace operators. Mathematische Nachrichten 2006,279(8):815-830. 10.1002/mana.200410396
-Laplace operators. Mathematische Nachrichten 2006,279(8):815-830. 10.1002/mana.200410396Gutiérrez CrE, Wheeden RL: Mean value and Harnack inequalities for degenerate parabolic equations. Colloquium Mathematicum 1990,60/61(1):157-194.
Gutiérrez CrE, Wheeden RL: Harnack's inequality for degenerate parabolic equations. Communications in Partial Differential Equations 1991,16(4-5):745-770. 10.1080/03605309108820776
Gutiérrez CrE, Wheeden RL: Bounds for the fundamental solution of degenerate parabolic equations. Communications in Partial Differential Equations 1992,17(7-8):1287-1307.
Ishige K: On the behavior of the solutions of degenerate parabolic equations. Nagoya Mathematical Journal 1999, 155: 1-26.
Pascucci A, Polidoro S: On the Harnack inequality for a class of hypoelliptic evolution equations. Transactions of the American Mathematical Society 2004,356(11):4383-4394. 10.1090/S0002-9947-04-03407-5
Krylov NV, Safonov MV: An estimate for the probability of a diffusion process hitting a set of positive measure. Doklady Akademii Nauk SSSR 1979,245(1):18-20.
Krylov NV, Safonov MV: A property of the solutions of parabolic equations with measurable coefficients. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya 1980,44(1):161-175, 239.
Safonov MV: Harnack's inequality for elliptic equations and Hölder property of their solutions. Zapiski Nauchnykh Seminarov Leningradskogo Otdeleniya Matematicheskogo Instituta imeni V. A. Steklova Akademii Nauk SSSR (LOMI) 1980, 96: 272-287, 312. Boundary value problems of mathematical physics and related questions in the theory of functions, 12
Nirenberg L: On nonlinear elliptic partial differential equations and Hölder continuity. Communications on Pure and Applied Mathematics 1953, 6: 103-156; addendum, 395. 10.1002/cpa.3160060105
Cordes HO: Über die erste Randwertaufgabe bei quasilinearen Differentialgleichungen zweiter Ordnung in mehr als zwei Variablen. Mathematische Annalen 1956,131(3):278-312. 10.1007/BF01342965
Landis EM: Harnack's inequality for second order elliptic equations of Cordes type. Doklady Akademii Nauk SSSR 1968, 179: 1272-1275.
Nirenberg L: On a generalization of quasi-conformal mappings and its application to elliptic partial differential equations. In Contributions to the Theory of Partial Differential Equations, Annals of Mathematics Studies, no. 33. Princeton University Press, Princeton, NJ, USA; 1954:95-100.
Landis EM: Uravneniya vtorogo poryadka ellipticheskogo i parabolicheskogo tipov. Izdat. "Nauka", Moscow, Russia; 1971:287.
Landis EM: Second Order Equations of Elliptic and Parabolic Type, Translations of Mathematical Monographs. Volume 171. American Mathematical Society, Providence, RI, USA; 1998:xii+203.
Evans LC: Classical solutions of fully nonlinear, convex, second-order elliptic equations. Communications on Pure and Applied Mathematics 1982,35(3):333-363. 10.1002/cpa.3160350303
Krylov NV: Boundedly inhomogeneous elliptic and parabolic equations. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya 1982,46(3):487-523, 670.
Krylov NV: Boundedly inhomogeneous elliptic and parabolic equations in a domain. Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya 1983,47(1):75-108.
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equations of Second Order, Classics in Mathematics. Springer, Berlin, Germany; 2001:xiv+517.
Caffarelli LA: Interior a priori estimates for solutions of fully nonlinear equations. Annals of Mathematics. Second Series 1989,130(1):189-213. 10.2307/1971480
Caffarelli LA, Cabré X: Fully Nonlinear Elliptic Equations, American Mathematical Society Colloquium Publications. Volume 43. American Mathematical Society, Providence, RI, USA; 1995:vi+104.
Yau Sh-T: Harmonic functions on complete Riemannian manifolds. Communications on Pure and Applied Mathematics 1975, 28: 201-228. 10.1002/cpa.3160280203
Hamilton RS: The Ricci flow on surfaces. In Mathematics and General Relativity (Santa Cruz, CA, 1986), Contemp. Math.. Volume 71. American Mathematical Society, Providence, RI, USA; 1988:237-262.
Chow B:The Ricci flow on the
 -sphere. Journal of Differential Geometry 1991,33(2):325-334.
-sphere. Journal of Differential Geometry 1991,33(2):325-334.Hamilton RS: The Harnack estimate for the Ricci flow. Journal of Differential Geometry 1993,37(1):225-243.
Andrews B: Harnack inequalities for evolving hypersurfaces. Mathematische Zeitschrift 1994,217(2):179-197.
Yau Sh-T: On the Harnack inequalities of partial differential equations. Communications in Analysis and Geometry 1994,2(3):431-450.
Chow B, Chu S-C: A geometric interpretation of Hamilton's Harnack inequality for the Ricci flow. Mathematical Research Letters 1995,2(6):701-718.
Hamilton RS: Harnack estimate for the mean curvature flow. Journal of Differential Geometry 1995,41(1):215-226.
Hamilton RS, Yau Sh-T: The Harnack estimate for the Ricci flow on a surface—revisited. Asian Journal of Mathematics 1997,1(3):418-421.
Chow B, Hamilton RS: Constrained and linear Harnack inequalities for parabolic equations. Inventiones Mathematicae 1997,129(2):213-238. 10.1007/s002220050162
Cao HD, Chow B, Chu SC, Yau Sh-T (Eds): Collected Papers on Ricci Flow, Series in Geometry and Topology. Volume 37. International Press, Somerville, Mass, USA; 2003:viii+539.
Müller R: Differential Harnack inequalities and the Ricci flow. EMS publishing house 2006., 2006, 100 pages:
Saloff-Coste L: A note on Poincaré, Sobolev, and Harnack inequalities. International Mathematics Research Notices 1992,1992(2):27-38. 10.1155/S1073792892000047
Grigor'yan AA: The heat equation on noncompact Riemannian manifolds. Matematicheskiĭ Sbornik 1991,182(1):55-87.
Saloff-Coste L: Parabolic Harnack inequality for divergence-form second-order differential operators. Potential Analysis 1995,4(4):429-467. 10.1007/BF01053457
Delmotte T: Parabolic Harnack inequality and estimates of Markov chains on graphs. Revista Matemática Iberoamericana 1999,15(1):181-232.
Sturm KT: Analysis on local Dirichlet spaces. III. The parabolic Harnack inequality. Journal de Mathématiques Pures et Appliquées. Neuvième Série 1996,75(3):273-297.
Barlow MT, Bass RF: Coupling and Harnack inequalities for Sierpiński carpets. Bulletin of the American Mathematical Society 1993,29(2):208-212. 10.1090/S0273-0979-1993-00424-5
Barlow MT, Bass RF: Brownian motion and harmonic analysis on Sierpinski carpets. Canadian Journal of Mathematics 1999,51(4):673-744. 10.4153/CJM-1999-031-4
Barlow MT, Bass RF: Divergence form operators on fractal-like domains. Journal of Functional Analysis 2000,175(1):214-247. 10.1006/jfan.2000.3597
Barlow MT, Bass RF: Stability of parabolic Harnack inequalities. Transactions of the American Mathematical Society 2004,356(4):1501-1533. 10.1090/S0002-9947-03-03414-7
Delmotte T: Graphs between the elliptic and parabolic Harnack inequalities. Potential Analysis 2002,16(2):151-168. 10.1023/A:1012632229879
Hebisch W, Saloff-Coste L: On the relation between elliptic and parabolic Harnack inequalities. Annales de l'Institut Fourier (Grenoble) 2001,51(5):1437-1481. 10.5802/aif.1861
Barlow MT: Some remarks on the elliptic Harnack inequality. Bulletin of the London Mathematical Society 2005,37(2):200-208. 10.1112/S0024609304003893
Bogdan K, Sztonyk P: Estimates of potential Kernel and Harnack's inequality for anisotropic fractional Laplacian. preprint, published as math.PR/0507579 in www.arxiv.org, 2005
Bass RF, Kassmann M: Harnack inequalities for non-local operators of variable order. Transactions of the American Mathematical Society 2005,357(2):837-850. 10.1090/S0002-9947-04-03549-4
Alexopoulos GK: Random walks on discrete groups of polynomial volume growth. Annals of Probability 2002,30(2):723-801.
Diaconis P, Saloff-Coste L: An application of Harnack inequalities to random walk on nilpotent quotients. Journal of Fourier Analysis and Applications 1995, 189-207.
Dodziuk J: Difference equations, isoperimetric inequality and transience of certain random walks. Transactions of the American Mathematical Society 1984,284(2):787-794. 10.1090/S0002-9947-1984-0743744-X
Grigor'yan A, Telcs A: Harnack inequalities and sub-Gaussian estimates for random walks. Mathematische Annalen 2002,324(3):521-556. 10.1007/s00208-002-0351-3
Lawler GrF: Estimates for differences and Harnack inequality for difference operators coming from random walks with symmetric, spatially inhomogeneous, increments. Proceedings of the London Mathematical Society. Third Series 1991,63(3):552-568. 10.1112/plms/s3-63.3.552
Lawler GrF, Polaski ThW: Harnack inequalities and difference estimates for random walks with infinite range. Journal of Theoretical Probability 1993,6(4):781-802. 10.1007/BF01049175
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kassmann, M. Harnack Inequalities: An Introduction. Bound Value Probl 2007, 081415 (2007). https://doi.org/10.1155/2007/81415
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/81415
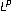 -integrability of Green's functions and fundamental solutions for elliptic and parabolic equations. Duke Mathematical Journal 1984,51(4):997-1016. 10.1215/S0012-7094-84-05145-7
-integrability of Green's functions and fundamental solutions for elliptic and parabolic equations. Duke Mathematical Journal 1984,51(4):997-1016. 10.1215/S0012-7094-84-05145-7 and the Harnack inequality. Calculus of Variations and Partial Differential Equations 2006,26(3):379-399. 10.1007/s00526-006-0022-4
and the Harnack inequality. Calculus of Variations and Partial Differential Equations 2006,26(3):379-399. 10.1007/s00526-006-0022-4 -elliptic operators. Communications in Partial Differential Equations 2003,28(11-12):1833-1862. 10.1081/PDE-120025487
-elliptic operators. Communications in Partial Differential Equations 2003,28(11-12):1833-1862. 10.1081/PDE-120025487 -Laplace operators. Mathematische Nachrichten 2006,279(8):815-830. 10.1002/mana.200410396
-Laplace operators. Mathematische Nachrichten 2006,279(8):815-830. 10.1002/mana.200410396 -sphere. Journal of Differential Geometry 1991,33(2):325-334.
-sphere. Journal of Differential Geometry 1991,33(2):325-334.