- Research Article
- Open access
- Published:
The Existence and Behavior of Solutions for Nonlocal Boundary Problems
Boundary Value Problems volume 2009, Article number: 484879 (2009)
Abstract
The purpose of this work is to investigate the uniqueness and existence of local solutions for the boundary value problem of a quasilinear parabolic equation. The result is obtained via the abstract theory of maximal regularity. Applications are given to some model problems in nonstationary radiative heat transfer and reaction-diffusion equation with nonlocal boundary flux conditions.
1. Introduction
The existence of solutions for quasilinear parabolic equation with boundary conditions and initial conditions can be discussed by maximal regularity, and more and more works on this field show that the maximal regularity method is efficient. Here we will use some of recently results developed by H. Amann to investigate a specific boundary value problems and then apply the existence theorem to two nonlocal problems.
This paper consists of three parts. In the next section we present and prove the existence and unique theorem of an abstract boundary problem. Then we give some applications of the results in Sections 3 and 4 to two reaction-diffusion model problems that arise from nonstationary radiative heat transfer in a system of moving absolutely black bodies and a reaction-diffusion equation with nonlocal boundary flux conditions.
2. Notations and Abstract Result
We consider the following quasilinear parabolic initial boundary value problem (IBVP for short):

where  is a bounded strictly Lipschitz domain with its boundary
is a bounded strictly Lipschitz domain with its boundary  and
and  ,
,  ,
,

and  is a second-order strongly elliptic differential operator with the boundary operator given by
is a second-order strongly elliptic differential operator with the boundary operator given by

The coefficient matrix  satisfies regularity conditions on
satisfies regularity conditions on  , respectively. The directional derivative
, respectively. The directional derivative  ,
,  is the outer unit-normal vector on
is the outer unit-normal vector on  ; the function
; the function  is defined as
is defined as  for
for  ;
;  denotes the trace operator.
denotes the trace operator.
We introduce precise assumptions:

where  ) are Carathéodory functions; that is,
) are Carathéodory functions; that is,  (resp.,
(resp.,  ) is measurable in
) is measurable in  (resp., in
(resp., in  for each
for each  and continuous in
and continuous in  for a.e.
for a.e.  (resp.,
(resp.,  . More general, the function
. More general, the function  can be a nonlocal function, for example,
can be a nonlocal function, for example,  or
or  .
.
Let  and
and  be Banach spaces, we introduce some notations as follows:
be Banach spaces, we introduce some notations as follows:
(i) ,
,  .
.  ,
,  .
.
(ii) for
for  ,
,  .
.
(iii) all continuous linear operators from
all continuous linear operators from  into
into  , and
, and  .
.
(iv) denotes the Nemytskii operator induced by
denotes the Nemytskii operator induced by  .
.
(v) denotes the set of all locally Lipschitz-continuous functions from
denotes the set of all locally Lipschitz-continuous functions from  into
into  .
.
(vi) ,
,  , and
, and  , denotes the set of all Carathéodory functions
, denotes the set of all Carathéodory functions  on
on  such that
such that  , and there exists a nondecreasing function
, and there exists a nondecreasing function  with
with

Particularly,  is independent of
is independent of  if
if  .
.
(vii) denotes the Sobolev-Slobodeckii space for
denotes the Sobolev-Slobodeckii space for  and
and  with the norm
with the norm  , especially,
, especially,  ; and
; and

(viii) ,
,  (
( is the set of integral numbers), is defined as
is the set of integral numbers), is defined as

where  ,
,  is the dual space of
is the dual space of  , and
, and  is the formally adjoint operator.
is the formally adjoint operator.
(x) if
if  and
and  is an interval in
is an interval in  .
.
(xi) denotes all maps
denotes all maps  possessing the property of maximal
possessing the property of maximal  regularity on
regularity on  with respect to
with respect to  , that is, given
, that is, given  , the initial problem
, the initial problem

has a unique solution  .
.
Now we turn to discuss the local existence result. We write

then,

Exactly,  as
as  , where
, where  denotes the Banach space of all functions being bounded and uniformly continuous in
denotes the Banach space of all functions being bounded and uniformly continuous in  . So, we will not emphasize it in the following.
. So, we will not emphasize it in the following.
A (weak) solution  of IBVP (2.1) is defined as a
of IBVP (2.1) is defined as a  function
function  ,
,  , satisfying
, satisfying

where  and
and  denote the obvious duality pairings on
denote the obvious duality pairings on  and
and  , respectively.
, respectively.
Set

After these preparations we introduce the following hypotheses:
(H1) and
and  .
.
(H2) with
with  , and there exists a
, and there exists a  such that
such that

 ,
,  with
with  , and
, and  .
.
(H3) for some
for some  .
.
Theorem 2.1.
Let assumptions (H1)-(H3) be satisfied. Then for each  the quasilinear problem (2.1) possesses a unique weak solution
the quasilinear problem (2.1) possesses a unique weak solution  for some
for some  .
.
Proof.
Recall that

The Nemytskii operator  is defined as
is defined as  . The fact
. The fact

shows the maximal regularity of the operator  . By [1, Theorem 2.1], if, for
. By [1, Theorem 2.1], if, for  ,
,  for some
for some  , then the existence and the uniqueness of a local solution will be proved.
, then the existence and the uniqueness of a local solution will be proved.
The remain work is to check the Lipschitz-continuity. Set

Then  . So, for
. So, for  with
with  we have
we have

From  , we infer that
, we infer that

where  . Note that
. Note that  , we can choose
, we can choose  such that
such that

On the other hand, the hypotheses guarantee that

Due to  and
and  , Hölder inequality follows that
, Hölder inequality follows that

The hypothesis of  means that one can find an
means that one can find an  such that
such that

Obviously, if  , the above inequality is followed from (2.20) immediately. Hence it follows from (2.19) and (2.22) that
, the above inequality is followed from (2.20) immediately. Hence it follows from (2.19) and (2.22) that

This ends the proof.
We apply the above theorem to the following two examples in next sections. For this, in the remainder we suppose that hypotheses (H1)-(H2) hold and that

3. A Radiative Heat Transfer Problem
We see a nonlinear initial-boundary value problem, which, in particular, describes a nonstationary radiative heat transfer in a system of absolutely black bodies (e.g., refer to [2]). A problem is

3.1. Local Solvability
We assume that (Hr)
(Hr1) ;
;
(Hr2) is locally Lipschitz continuous and
is locally Lipschitz continuous and  .
.
Theorem 3.1.
Let assumptions (H1)-(H2) and (Hr) be satisfied. Then problem (3.1), for all  , has a unique
, has a unique  for some
for some  .
.
Proof.
Note that the embedding (2.14) holds:

Hence Theorem 2.1 implies the result immediately.
In fact, Amosov proved in 2005 the uniqueness of the solution for a simple case, that is, problem in which the matrix  is independent of
is independent of  (see [2, Theorem 1.4]). In this paper, we also can get the positivity of the solution and the estimates of the solution in
(see [2, Theorem 1.4]). In this paper, we also can get the positivity of the solution and the estimates of the solution in  and
and  in this part. We have tried to achieve the global existence, but it is still an open problem.
in this part. We have tried to achieve the global existence, but it is still an open problem.
In the rest of this section, we always assume that (H1)-(H2) and (Hr) hold.
3.2. Positivity
Assume that
(H+) is nondecreasing with
is nondecreasing with  , and
, and

Theorem 3.2.
Let assumption ( ) be satisfied. If
) be satisfied. If  is nonnegative, then the solution
is nonnegative, then the solution  of problem (3.1) is also nonnegative.
of problem (3.1) is also nonnegative.
Proof.
Put  . Multiplying the equation with
. Multiplying the equation with  and integrating over
and integrating over  , we have
, we have

By using the assumption of ( ), we can get following equality:
), we can get following equality: 

So,

At the last inequality, the monotonity of  on
on  and the restriction
and the restriction  are used. Therefore,
are used. Therefore,

If  , then
, then  . The assertion follows.
. The assertion follows.
3.3. 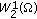 -norm
-norm
We denote by  the maximal interval of the solution of problem (3.1).
the maximal interval of the solution of problem (3.1).
Lemma 3.3.
There exists a constant  such that the solution
such that the solution  of problem (3.1) satisfies
of problem (3.1) satisfies

Proof.
Multiplying by  and integrating over
and integrating over  , we have
, we have

That is,

As similar as the inequality (3.6), we have

Hence,

By using the embedding  and letting
and letting  small enough, it is easy to get that
small enough, it is easy to get that

3.4.  -norm
-norm
Theorem 3.4.
If  and
and  , then the solution
, then the solution  of problem (3.1) is bounded with its
of problem (3.1) is bounded with its  -norm for all
-norm for all  .
.
Proof.
From the hypothesis (H1) and embedding (2.10), one has that  and
and  . By multiplying with
. By multiplying with  and
and  ) and integrating over
) and integrating over  , we have
, we have

That is,

But,

 Therefore,
Therefore,

where Young's inequality,  , has been used at the last inequality. We apply the embedding
, has been used at the last inequality. We apply the embedding  again with
again with  and choose
and choose  small enough, then we attain the following inequality:
small enough, then we attain the following inequality:

By Gronwall's inequality, the inequality (3.18) becomes

Set  , then we deduce that
, then we deduce that

Let  the inequality (3.20) implies
the inequality (3.20) implies

The claim follows.
One immediate consequence of the above theorem is.
Corollary 3.5.
The  -norm of the solution
-norm of the solution  , that is,
, that is,  , of problem (3.1) is nonincreasing if
, of problem (3.1) is nonincreasing if  .
.
4. A Nonlocal Boundary Value Problem
We now consider the problem (2.1) with the following boundary value condition:

The function  in (4.1) can be in nonlocal form.
in (4.1) can be in nonlocal form.
IBVP (2.1) with a nonlocal term stands, for example, for a model problem arising from quasistatic thermoelasticity. Results on linear problems can be found in [3–5]. As far as we know, this kind of nonlocal boundary condition appeared first in 1952 in a paper [6] by W. Feller who discussed the existence of semigroups. There are other problems leading to this boundary condition, for example, control theory (see [7–12] etc.). Some other fields such as environmental science [13] and chemical diffusion [14] also give rise to such kinds of problems. We do not give further comments here.
Carl and Heikkilä [15] proved the existence of local solutions of the semilinear problem by using upper and lower solutions and pseudomonotone operators. But their results based on the monotonicity hypotheses of  ,
,  , and
, and  with respect to
with respect to  .
.
In this section, we assume that (H1) and (H2) always hold and assume that
(Hn1) and
and  for some
for some  ;
;
(Hn2) ,
,  satisfies the Carathéodory condition on
satisfies the Carathéodory condition on  and
and  .
.
By the embedding theorem and Theorem 2.1, we get immediately.
Theorem 4.1.
Suppose hypotheses of (Hn) satisfy. Then problem (2.1), for all  , with
, with  defined in (4.1) has a unique
defined in (4.1) has a unique  for some
for some  .
.
For the simplicity in expression, we turn to consider a problem with nonlocal boundary value

where

and
(Hk)The function  satisfies the Carathéodory condition on
satisfies the Carathéodory condition on  ,
, and f
and f  with
with

Theorem 4.2.
Let assumption (Hk) be satisfied. Then Problem (4.2), for any  , has a unique solution
, has a unique solution  for some
for some  .
.
Proof.
First, we see that

Choose  such that
such that  , then
, then  . Consequently, there exists
. Consequently, there exists  such that
such that

Similarly, from  we have
we have

Combining two inequalities (4.6) and (4.7), we obtain that

The claim follows immediately from Theorem 4.1.
A special case of problem (4.2) is

That is,  and
and  in (4.9) are independent of gradient
in (4.9) are independent of gradient  .
.
4.1. 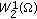 -norm
-norm
In order to discuss the global existence of solution, in the rest of this section we assume the following.
(Hkl)Suppose there exists a continuous function  such that
such that

Lemma 4.3.
There exists a constant  such that the solution of problem (4.9) satisfies
such that the solution of problem (4.9) satisfies

Proof.
We multiply the first equation in (4.9) with  and then integrate over
and then integrate over  , and we find that
, and we find that

Since  for
for  , by interpolation inequality and Young's inequality we have that
, by interpolation inequality and Young's inequality we have that

Apply Young's inequality again and then choose  small enough (
small enough ( ); it is not difficult to get
); it is not difficult to get

where  for
for  . Therefore, by multiplying with
. Therefore, by multiplying with  and integrating over
and integrating over  , the inequality (4.14) follows the claim.
, the inequality (4.14) follows the claim.
4.2. 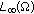 -norm
-norm
Lemma 4.4.
Let assumptions of Lemma 4.3 be satisfied. If  , then the solution
, then the solution  of problem (4.9) satisfies
of problem (4.9) satisfies

Proof.
We multiply the first equation in (4.9) with  and integrate over
and integrate over  , then we reach that
, then we reach that

As the same as the inequality (4.13), we have

Hence,

We might as well assume that  , so,
, so,

The boundedness of solution  for
for  is used in above deduction.
is used in above deduction.
Let  (
( small enough, then we have
small enough, then we have

Multiplying with  , then integrating over
, then integrating over  , we obtain that
, we obtain that

By a similar limitation process as in (3.21), we get

This closes the end of proof.
4.3. Decay Behavior
In order to investigate the decay behavior of solution for problem (4.9), we assume that
(Hkd) there are two continuous function  and
and  (
( ) such that
) such that

for all  .
.
Theorem 4.5.
Let the assumption (Hkd) be satisfied and,  be the solution of problem (4.9) with
be the solution of problem (4.9) with  . Then
. Then  decay to zero as
decay to zero as  for some small functions
for some small functions  .
.
Proof.
We use  to multiply the first equation in the system (4.9) and then integrate over
to multiply the first equation in the system (4.9) and then integrate over  . Thus, we get that
. Thus, we get that

In the above process the inequality (4.13) is used. If we choose  as
as

then

This ends the proof.
Moreover, one can verify that  also decay to zero (as
also decay to zero (as  ) if
) if 
References
Amann H: Quasilinear parabolic problems via maximal regularity. Advances in Differential Equations 2005, 10(10):1081–1110.
Amosov AA: Global solvability of a nonlinear nonstationary problem with a nonlocal boundary condition of radiative heat transfer type. Differential Equations 2005, 41(1):96–109. 10.1007/s10625-005-0139-9
Day WA: A decreasing property of solutions of parabolic equations with applications to thermoelasticity. Quarterly of Applied Mathematics 1983, 40(4):468–475.
Friedman A: Monotonic decay of solutions of parabolic equations with nonlocal boundary conditions. Quarterly of Applied Mathematics 1986, 44(3):401–407.
Muraveĭ LA, Filinovskiĭ AV: On a problem with nonlocal boundary condition for a parabolic equation. Mathematics of the USSR-Sbornik 1993, 74(1):219–249. 10.1070/SM1993v074n01ABEH003345
Feller W: The parabolic differential equations and the associated semi-groups of transformations. Annals of Mathematics 1952, 55(3):468–519. 10.2307/1969644
Lions JL, Magenes E: Non-Homogeneous Boundary Value Problems and Applications. Vol. I. Springer, Berlin, Germany; 1972:xvi+357.
Lions JL, Magenes E: Non-Homogeneous Boundary Value Problems and Applications. Vol. II. Springer, Berlin, Germany; 1972:xi+242.
Lasiecka I: Unified theory for abstract parabolic boundary problems—a semigroup approach. Applied Mathematics and Optimization 1980, 6(1):287–333. 10.1007/BF01442900
Amann H: Feedback stabilization of linear and semilinear parabolic systems. In Semigroup Theory and Applications (Trieste, 1987), Lecture Notes in Pure and Applied Mathematics. Volume 116. Edited by: Clement P, Invernizzi S, Mitidieri E, Vrabie II. Dekker, New York, NY, USA; 1989:21–57.
Agarwal RP, Bohner M, Shakhmurov VB: Linear and nonlinear nonlocal boundary value problems for differential-operator equations. Applicable Analysis 2006, 85(6–7):701–716. 10.1080/00036810500533153
Ashyralyev A: Nonlocal boundary-value problems for abstract parabolic equations: well-posedness in Bochner spaces. Journal of Evolution Equations 2006, 6(1):1–28. 10.1007/s00028-005-0194-y
Capasso V, Kunisch K: A reaction-diffusion system modelling man-environment epidemics. Annals of Differential Equations 1985, 1(1):1–12.
Taira K: Diffusion Processes and Partial Differential Equations. Academic Press, Boston, Mass, USA; 1988:xviii+452.
Carl S, Heikkilä S: Discontinuous reaction-diffusion equations under discontinuous and nonlocal flux conditions. Mathematical and Computer Modelling 2000, 32(11–13):1333–1344.
Acknowledgments
The first author wishes to thank Professor Herbert Amann for many useful discussions concerning the problem of this paper. The author also want to thank the referees' suggestions. This work is supported partly by the National NSF of China (Grant nos. 10572080 and 10671118) and by Shanghai Leading Academic Discipline Project (no. J50101).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, Y., Zheng, S. The Existence and Behavior of Solutions for Nonlocal Boundary Problems. Bound Value Probl 2009, 484879 (2009). https://doi.org/10.1155/2009/484879
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/484879
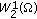 -norm
-norm -norm
-norm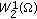 -norm
-norm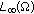 -norm
-norm