- Research Article
- Open access
- Published:
Interior Controllability of a 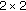 Reaction-Diffusion System with Cross-Diffusion Matrix
Reaction-Diffusion System with Cross-Diffusion Matrix
Boundary Value Problems volume 2009, Article number: 560407 (2009)
Abstract
We prove the interior approximate controllability for the following  reaction-diffusion system with cross-diffusion matrix
reaction-diffusion system with cross-diffusion matrix  in
in  ,
,  in
in  ,
,  , on
, on  ,
,  ,
,  ,
,  , where
, where  is a bounded domain in
is a bounded domain in  ,
,  , the
, the  diffusion matrix
diffusion matrix  has semisimple and positive eigenvalues
has semisimple and positive eigenvalues  ,
,  is an arbitrary constant,
is an arbitrary constant,  is an open nonempty subset of
is an open nonempty subset of  ,
,  denotes the characteristic function of the set
denotes the characteristic function of the set  , and the distributed controls
, and the distributed controls  . Specifically, we prove the following statement: if
. Specifically, we prove the following statement: if  (where
(where  is the first eigenvalue of
is the first eigenvalue of  ), then for all
), then for all  and all open nonempty subset
and all open nonempty subset  of
of  the system is approximately controllable on
the system is approximately controllable on  .
.
1. Introduction
In this paper we prove the interior approximate controllability for the following  reaction-diffusion system with cross-diffusion matrix
reaction-diffusion system with cross-diffusion matrix

where  is a bounded domain in
is a bounded domain in  (
( ),
),  , the
, the  diffusion matrix
diffusion matrix

has semisimple and positive eigenvalues,  is an arbitrary constant,
is an arbitrary constant,  is an open nonempty subset of
is an open nonempty subset of  ,
,  denotes the characteristic function of the set
denotes the characteristic function of the set  , and the distributed controls
, and the distributed controls  . Specifically, we prove the following statement: if
. Specifically, we prove the following statement: if  (the first eigenvalue of
(the first eigenvalue of  ), then for all
), then for all  and all open nonempty subset
and all open nonempty subset  of
of  , the system is approximately controllable on
, the system is approximately controllable on  .
.
When  this system takes the following particular form:
this system takes the following particular form:

This paper has been motivated by the work done Badraoui in [1], where author studies the asymptotic behavior of the solutions for the system (1.3) on the unbounded domain  . That is to say, he studies the system:
. That is to say, he studies the system:

supplemented with the initial conditions:

where the diffusion coefficients  and
and  are assumed positive constants, while the diffusion coefficients
are assumed positive constants, while the diffusion coefficients  ,
,  and the coefficient
and the coefficient  are arbitrary constants. He assume also the following three conditions:
are arbitrary constants. He assume also the following three conditions:
(H1) ,
,  and
and  ,
,
(H2) where
where  is the space of bounded and uniformly continuous real-valued functions,
is the space of bounded and uniformly continuous real-valued functions,
(H3) and
and  , for all
, for all  and
and  . Moreover,
. Moreover,  and
and  are locally Lipshitz; namely, for all
are locally Lipshitz; namely, for all  and all constant
and all constant  , there exist a constant
, there exist a constant  such that
such that

is verified for all  ,
,  with
with  ,
,  and
and  .
.
We note that the hypothesis (H1) implies that the eigenvalues of the matrix  are simple and positive. But, this condition is not necessary for the eigenvalues of
are simple and positive. But, this condition is not necessary for the eigenvalues of  to be positive, in fact we can find matrices
to be positive, in fact we can find matrices  with
with  and
and  been negative and having positive eigenvalues. For example, one can consider the following matrix:
been negative and having positive eigenvalues. For example, one can consider the following matrix:

whose eigenvalues are  and
and  .
.
The system (1.1) can be written in the following matrix form:

where  , the distributed controls
, the distributed controls  , and
, and  is the identity matrix of dimension
is the identity matrix of dimension  .
.
Our technique is simple and elegant from mathematical point of view, it rests on the shoulders of the following fundamental results.
Theorem 1.1.
The eigenfunctions of  with Dirichlet boundary condition are real analytic functions.
with Dirichlet boundary condition are real analytic functions.
Theorem 1.2 (see [2, Theorem 1.23, page 20]).
Suppose  is open, nonempty, and connected set, and
is open, nonempty, and connected set, and  is real analytic function in
is real analytic function in  with
with  on a nonempty open subset
on a nonempty open subset  of
of  . Then,
. Then,  in
in  .
.
Lemma 1.3 (see [3, Lemma 3.14, page 62]).
Let  and
and  be two sequences of real numbers such that
be two sequences of real numbers such that  . Then
. Then

if and only if

Finally, with this technique those young mathematicians who live in remote and inhospitable places, far from major research centers in the world, can also understand and enjoy the interior controllability with a minor effort.
2. Abstract Formulation of the Problem
In this section we choose a Hilbert space where system (1.8) can be written as an abstract differential equation; to this end, we consider the following notations:
Let us consider the Hilbert space  and
and  the eigenvalues of
the eigenvalues of  , each one with finite multiplicity
, each one with finite multiplicity  equal to the dimension of the corresponding eigenspace. Then, we have the following well-known properties (see [3, pages 45-46]).
equal to the dimension of the corresponding eigenspace. Then, we have the following well-known properties (see [3, pages 45-46]).
(i)There exists a complete orthonormal set  of eigenvectors of
of eigenvectors of  .
.
(ii)For all  , we have
, we have

where  is the inner product in
is the inner product in  and
and

So,  is a family of complete orthogonal projections in
is a family of complete orthogonal projections in  and
and  ,
, 
(iii) generates an analytic semigroup
generates an analytic semigroup  given by
given by

Now, we denote by  the Hilbert space
the Hilbert space  and define the following operator:
and define the following operator:

with  . Therefore, for all
. Therefore, for all  , we obtain
, we obtain


where

is a family of complete orthogonal projections in  .
.
Consequently, system (1.8) can be written as an abstract differential equation in  :
:

where  ,
,  , and
, and  ,
,  is a bounded linear operator.
is a bounded linear operator.
Now, we will use the following Lemma from [4] to prove the following theorem.
Lemma 2.1.
Let  be a Hilbert separable space and
be a Hilbert separable space and  ,
,  two families of bounded linear operator in
two families of bounded linear operator in  , with
, with  a family of complete orthogonal projection such that
a family of complete orthogonal projection such that

Define the following family of linear operators:

Then the following hold.
(a) is a linear and bounded operator if
is a linear and bounded operator if  ,
,  , with
, with  , continuous for
, continuous for  .
.
(b)Under the above (a),  is a strongly continuous semigroup in the Hilbert space
is a strongly continuous semigroup in the Hilbert space  , whose infinitesimal generator
, whose infinitesimal generator  is given by
is given by

with

(c)The spectrum  of
of  is given by
is given by

where  .
.
Theorem 2.2.
The operator  define by (2.5) is the infinitesimal generator of a strongly continuous semigroup
define by (2.5) is the infinitesimal generator of a strongly continuous semigroup  given by:
given by:

where  and
and  with
with

Moreover, if  , then there exists
, then there exists  such that
such that

Proof.
In order to apply the foregoing Lemma, we observe that  can be written as follows:
can be written as follows:

with

Therefore,  with
with

Clearly that  is a bounded linear operator (linear and continuous). That is, there exists
is a bounded linear operator (linear and continuous). That is, there exists  such that
such that

In fact,  .
.
Now, we have to verify condition (a) of Lemma 2.1. To this end, without loss of generality, we will suppose that  . Then, there exists a set
. Then, there exists a set  of complementary projections on
of complementary projections on  such that
such that

Hence,

This implies the existence of positive numbers  such that
such that

Therefore,  generates a strongly continuous semigroup
generates a strongly continuous semigroup  given by (2.14).
given by (2.14).
Finally, if  , then
, then

and using (2.14) we obtain (2.16).
3. Proof of the Main Theorem
In this section we will prove the main result of this paper on the controllability of the linear system (2.8). But, before we will give the definition of approximate controllability for this system. To this end, for all  and
and  , the initial value problem
, the initial value problem

where the control function  belonging to
belonging to  admits only one mild solution given by
admits only one mild solution given by

Definition 3.1 (approximate controllability).
The system (2.8) is said to be approximately controllable on  if for every
if for every  ,
,  there exists
there exists  such that the solution
such that the solution  of (3.2) corresponding to
of (3.2) corresponding to  verifies:
verifies:

The following result can be found in [5] for the general evolution equation:

where  ,
,  are Hilbert spaces,
are Hilbert spaces,  is the infinitesimal generator of strongly continuous semigroup
is the infinitesimal generator of strongly continuous semigroup  in
in  , the control function
, the control function  belongs to
belongs to  .
.
Theorem 3.2.
System (3.4) is approximately controllable on  if and only if
if and only if

Now, one is ready to formulate and prove the main theorem of this work.
Theorem 3.3 (main theorem).
If  , then for all
, then for all  and all open nonempty subset
and all open nonempty subset  of
of  the system, (2.8) is approximately controllable on
the system, (2.8) is approximately controllable on  .
.
Proof.
We will apply Theorem 3.2 to prove the approximate controllability of system (2.8). With this purpose, we observe that

On the other hand,

Without lose of generality, we will suppose that  . Then, there exists a set
. Then, there exists a set  of complementary projections on
of complementary projections on  such that
such that

Hence,

Therefore,

where  .
.
Now, suppose for  that
that  , for all
, for all  . Then,
. Then,

Clearly that,  is a decreasing sequence. Then, from Lemma 1.3, we obtain for all x
is a decreasing sequence. Then, from Lemma 1.3, we obtain for all x  that
that

Since  , we get that
, we get that

On the other hand, from Theorem 1.1 we know that  are analytic functions, which implies the analyticity of
are analytic functions, which implies the analyticity of  ,
,  . Then, from Theorem 1.2 we get that
. Then, from Theorem 1.2 we get that

Hence  ,
,  , which implies that
, which implies that  . This completes the proof of the main theorem.
. This completes the proof of the main theorem.
References
Badraoui S: Asymptotic behavior of solutions to a
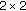 reaction-diffusion system with a cross diffusion matrix on unbounded domains. Electronic Journal of Differential Equations 2006, 2006(61):1–13.
reaction-diffusion system with a cross diffusion matrix on unbounded domains. Electronic Journal of Differential Equations 2006, 2006(61):1–13.Axler S, Bourdon P, Ramey W: Harmonic Function Theory, Graduate Texts in Mathematics. Volume 137. Springer, New York, NY, USA; 1992:xii+231.
Curtain RF, Pritchard AJ: Infinite Dimensional Linear Systems Theory, Lecture Notes in Control and Information Sciences. Volume 8. Springer, Berlin, Germany; 1978:vii+297.
Leiva H: A lemma on
 -semigroups and applications PDEs systems. Quaestiones Mathematicae 2003, 26(3):247–265. 10.2989/16073600309486057
-semigroups and applications PDEs systems. Quaestiones Mathematicae 2003, 26(3):247–265. 10.2989/16073600309486057Curtain RF, Zwart H: An Introduction to Infinite-Dimensional Linear Systems Theory, Texts in Applied Mathematics. Volume 21. Springer, New York, NY, USA; 1995:xviii+698.
Acknowledgment
This work was supported by the CDHT-ULA-project: 1546-08-05-B.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Larez, H., Leiva, H. Interior Controllability of a 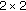 Reaction-Diffusion System with Cross-Diffusion Matrix.
Bound Value Probl 2009, 560407 (2009). https://doi.org/10.1155/2009/560407
Reaction-Diffusion System with Cross-Diffusion Matrix.
Bound Value Probl 2009, 560407 (2009). https://doi.org/10.1155/2009/560407
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/560407
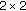 reaction-diffusion system with a cross diffusion matrix on unbounded domains. Electronic Journal of Differential Equations 2006, 2006(61):1–13.
reaction-diffusion system with a cross diffusion matrix on unbounded domains. Electronic Journal of Differential Equations 2006, 2006(61):1–13. -semigroups and applications PDEs systems. Quaestiones Mathematicae 2003, 26(3):247–265. 10.2989/16073600309486057
-semigroups and applications PDEs systems. Quaestiones Mathematicae 2003, 26(3):247–265. 10.2989/16073600309486057