- Research Article
- Open access
- Published:
Blow-Up Results for a Nonlinear Hyperbolic Equation with Lewis Function
Boundary Value Problems volume 2009, Article number: 691496 (2009)
Abstract
The initial boundary value problem for a nonlinear hyperbolic equation with Lewis function in a bounded domain is considered. In this work, the main result is that the solution blows up in finite time if the initial data possesses suitable positive energy. Moreover, the estimates of the lifespan of solutions are also given.
1. Introduction
Let  be a bounded domain in
be a bounded domain in  with smooth boundary
with smooth boundary  . We consider the initial boundary value problem for a nonlinear hyperbolic equation with Lewis function
. We consider the initial boundary value problem for a nonlinear hyperbolic equation with Lewis function  which depends on spacial variable:
which depends on spacial variable:



where  ,
,  ,
,  , and
, and  is a continuous function.
is a continuous function.
The large time behavior of solutions for nonlinear evolution equations has been considered by many authors (for the relevant references one may consult with [1–14].)
In the early 1970s, Levine [3] considered the nonlinear wave equation of the form

in a Hilbert space where  are
are  are positive linear operators defined on some dense subspace of the Hilbert space and
are positive linear operators defined on some dense subspace of the Hilbert space and  is a gradient operator. He introduced the concavity method and showed that solutions with negative initial energy blow up in finite time. This method was later improved by Kalantarov and Ladyzheskaya [4] to accommodate more general cases.
is a gradient operator. He introduced the concavity method and showed that solutions with negative initial energy blow up in finite time. This method was later improved by Kalantarov and Ladyzheskaya [4] to accommodate more general cases.
Very recently, Zhou [10] considered the initial boundary value problem for a quasilinear parabolic equation with a generalized Lewis function which depends on both spacial variable and time. He obtained the blowup of solutions with positive initial energy. In the case with zero initial energy Zhou [11] obtained a blow-up result for a nonlinear wave equation in  . A global nonexistence result for a semilinear Petrovsky equation was given in [14].
. A global nonexistence result for a semilinear Petrovsky equation was given in [14].
In this work, we consider blow-up results in finite time for solutions of problem (1.1)-(1.3) if the initial datas possesses suitable positive energy and obtain a precise estimate for the lifespan of solutions. The proof of our technique is similar to the one in [10]. Moreover, we also show the blowup of solution in finite time with nonpositive initial energy.
Throughout this paper  denotes the usual norm of
denotes the usual norm of  .
.
The source term  in (1.1) with the primitive
in (1.1) with the primitive

satisfies


Let  be the best constant of Sobolev embedding inequality
be the best constant of Sobolev embedding inequality

from  to
to  .
.
We need the following lemma in [4, Lemma 2.1].
Lemma 1.1.
Suppose that a positive, twice differentiable function  satisfies for
satisfies for  the inequality
the inequality

If  ,
,  , then
, then

2. Blow-Up Results
We set

The corresponding energy to the problem (1.1)-(1.3) is given by

and one can find that  easily from
easily from

whence

We note that from (1.6) and (1.7), we have

and by Sobolev inequality (1.8),  ,
,  , where
, where

Note that  has the maximum value
has the maximum value  at
at  which are given in (2.1).
which are given in (2.1).
Adapting the idea of Zhou [10], we have the following lemma.
Lemma 2.1.
Suppose that  and
and  . Then
. Then

for all  .
.
Theorem 2.2.
For  , suppose that
, suppose that  and
and  satisfy
satisfy

If  , then the global solution of the problem (1.1)–(1.3) blows up in finite time and the lifespan
, then the global solution of the problem (1.1)–(1.3) blows up in finite time and the lifespan

Proof.
To prove the theorem, it suffices to show that the function

satisfies the hypotheses of the Lemma 1.1, where  ,
,  and
and  to be determined later. To achieve this goal let us observe
to be determined later. To achieve this goal let us observe

Hence,

Let us compute the derivatives  and
and  . Thus one has
. Thus one has

and

for all  . In the above assumption (1.7), the definition of energy functionals (2.2) and (2.4) has been used. Then, due to (2.1) and (2.7) and taking
. In the above assumption (1.7), the definition of energy functionals (2.2) and (2.4) has been used. Then, due to (2.1) and (2.7) and taking  ,
,

Hence  for all
for all  and by assumption (2.8) we have
and by assumption (2.8) we have

Therefore  for all
for all  and by the construction of
and by the construction of  , it is clearly that
, it is clearly that

whence,  . Thus for all
. Thus for all  , from (2.13), (2.15), and (2.17) we obtain
, from (2.13), (2.15), and (2.17) we obtain

which implies

Then using Lemma 1.1, one obtain that  as
as

Now, we are in a position to choose suitable  and
and  . Let
. Let  be a number that depends on
be a number that depends on  ,
,  ,
,  , and
, and  as
as

To choose  , we may fix
, we may fix  as
as

Thus, for  the lifespan
the lifespan  is estimated by
is estimated by

which completes the proof.
Theorem 2.3.
Assume that  and the following conditions are valid:
and the following conditions are valid:

Then the corresponding solution to (1.1)–(1.3) blows up in finite time.
Proof.
Let

then


where the left-hand side of assumption (1.7) and the energy functional (2.2) have been used. Taking the inequality (2.27) and integrating this, we obtain

By using Poincare-Friedrich's inequality

and Holder's inequality


where  . Using (2.30) and (2.31), we find from (2.28) that
. Using (2.30) and (2.31), we find from (2.28) that

Since  as
as  so, there must be a
so, there must be a  such that
such that

By inequality

and by virtue of (2.33) and using (2.32), we get

where

Therefore, there exits a positive constant

such that

This completes the proof.
References
Áng DD, Dinh APN: On the strongly damped wave equation: .
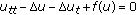 SIAM Journal on Mathematical Analysis 1988, 19(6):1409–1418. 10.1137/0519103
SIAM Journal on Mathematical Analysis 1988, 19(6):1409–1418. 10.1137/0519103Nishihara K: Asymptotic behavior of solutions of quasilinear hyperbolic equations with linear damping. Journal of Differential Equations 1997, 137(2):384–395. 10.1006/jdeq.1997.3268
Levine HA: Instability and nonexistence of global solutions to nonlinear wave equations of the form .
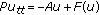 Transactions of the American Mathematical Society 1974, 192: 1–21.
Transactions of the American Mathematical Society 1974, 192: 1–21.Kalantarov VK, Ladyzhenskaya OA: The occurrence of collapase for quasi-linear equations of parabolic and hyperbolic type. Journal of Soviet Mathematics 1978, 10: 53–70. 10.1007/BF01109723
Can M, Park SR, Aliyev F: Nonexistence of global solutions of some quasilinear hyperbolic equations. Journal of Mathematical Analysis and Applications 1997, 213(2):540–553. 10.1006/jmaa.1997.5557
Ono K: Global existence, asymptotic behaviour, and global non-existence of solutions for damped non-linear wave equations of Kirchhoff type in the whole space. Mathematical Methods in the Applied Sciences 2000, 23(6):535–560. 10.1002/(SICI)1099-1476(200004)23:6<535::AID-MMA125>3.0.CO;2-H
Tan Z: The reaction-diffusion equation with Lewis function and critical Sobolev exponent. Journal of Mathematical Analysis and Applications 2002, 272(2):480–495. 10.1016/S0022-247X(02)00166-X
Zhijian Y: Global existence, asymptotic behavior and blowup of solutions for a class of nonlinear wave equations with dissipative term. Journal of Differential Equations 2003, 187(2):520–540. 10.1016/S0022-0396(02)00042-6
Polat N, Kaya D, Tutalar HI: Blow-up of solutions for a class of nonlinear wave equations. Proceedings of the International Conference on Dynamic Systems and Applications, July 2004 572–576.
Zhou Y: Global nonexistence for a quasilinear evolution equation with a generalized Lewis function. Journal for Analysis and Its Applications 2005, 24(1):179–187.
Zhou Y: A blow-up result for a nonlinear wave equation with damping and vanishing initial energy in .
 Applied Mathematics Letters 2005, 18(3):281–286. 10.1016/j.aml.2003.07.018
Applied Mathematics Letters 2005, 18(3):281–286. 10.1016/j.aml.2003.07.018Wu S-T, Tsai L-Y: Blow-up of solutions for evolution equations with nonlinear damping. Applied Mathematics E-Notes 2006, 6: 58–65.
Messaoudi SA, Houari BS: A blow-up result for a higher-order nonlinear Kirchhoff-type hyperbolic equation. Applied Mathematics Letters 2007, 20(8):866–871. 10.1016/j.aml.2006.08.018
Chen W, Zhou Y: Global nonexistence for a semilinear Petrovsky equation. Nonlinear Analysis: Theory, Methods & Applications 2009, 70(9):3203–3208. 10.1016/j.na.2008.04.024
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tahamtani, F. Blow-Up Results for a Nonlinear Hyperbolic Equation with Lewis Function. Bound Value Probl 2009, 691496 (2009). https://doi.org/10.1155/2009/691496
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/691496
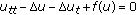 SIAM Journal on Mathematical Analysis 1988, 19(6):1409–1418. 10.1137/0519103
SIAM Journal on Mathematical Analysis 1988, 19(6):1409–1418. 10.1137/0519103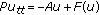 Transactions of the American Mathematical Society 1974, 192: 1–21.
Transactions of the American Mathematical Society 1974, 192: 1–21. Applied Mathematics Letters 2005, 18(3):281–286. 10.1016/j.aml.2003.07.018
Applied Mathematics Letters 2005, 18(3):281–286. 10.1016/j.aml.2003.07.018