- Research Article
- Open access
- Published:
Stagnation Zones for 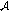 -Harmonic Functions on Canonical Domains
-Harmonic Functions on Canonical Domains
Boundary Value Problems volume 2009, Article number: 853607 (2010)
Abstract
We study stagnation zones of  -harmonic functions on canonical domains in the Euclidean
-harmonic functions on canonical domains in the Euclidean  -dimensional space. Phragmén-Lindelöf type theorems are proved.
-dimensional space. Phragmén-Lindelöf type theorems are proved.
1. Introduction
In this article we investigate solutions of the  -Laplace equation on canonical domains in the
-Laplace equation on canonical domains in the  -dimensional Euclidean space.
-dimensional Euclidean space.
Suppose that  is a domain in
is a domain in  , and let
, and let  be a function. For
be a function. For  , a subset
, a subset  is called
is called  -zone (stagnation zone with the deviation
-zone (stagnation zone with the deviation ) of
) of  if there exists a constant
if there exists a constant  such that the difference between
such that the difference between  and the function
and the function  is smaller than
is smaller than  on
on  . We may, for example, consider difference in the sense of the sup norm
. We may, for example, consider difference in the sense of the sup norm

the  -norm
-norm

or the Sobolev norm

where  is the
is the  -dimensional Hausdorff measure in
-dimensional Hausdorff measure in  .
.
For discussion about the history of the question, recent results and applications the reader is referred to [1, 2].
Some estimates of stagnation zone sizes for solutions of the  -Laplace equation on locally Lipschitz surfaces and behavior of solutions in stagnation zones were given in [3]. In this paper we consider solutions of the
-Laplace equation on locally Lipschitz surfaces and behavior of solutions in stagnation zones were given in [3]. In this paper we consider solutions of the  -Laplace equation in subdomains of
-Laplace equation in subdomains of  of a special form, canonical domains. In two-dimensional case, such domains are sectors and strips. In higher dimensions, they are conical and cylindrical regions. The special form of domains allows us to obtain more precise results.
of a special form, canonical domains. In two-dimensional case, such domains are sectors and strips. In higher dimensions, they are conical and cylindrical regions. The special form of domains allows us to obtain more precise results.
Below we study stagnation zones of generalized solutions of the  -Laplace equation
-Laplace equation

(see [4]) with boundary conditions of types (see Definitions 1.1 and 1.2 below)

on canonical domains in the Euclidean  -dimensional space, where
-dimensional space, where  is a closed subset of
is a closed subset of  . We will prove Phragmén-Lindelöf type theorems for solutions of the
. We will prove Phragmén-Lindelöf type theorems for solutions of the  -Laplace equation with such boundary conditions.
-Laplace equation with such boundary conditions.
1.1. Canonical Domains
Let  . Fix an integer
. Fix an integer  ,
,  and set
and set

We call the set

a  -ball and
-ball and

a  -sphere in
-sphere in  . In particular, the symbol
. In particular, the symbol  denotes the
denotes the  -sphere with the radius
-sphere with the radius  , that is, the set
, that is, the set

For every  , we set
, we set

Let  be fixed, and let (see Figure 1)
be fixed, and let (see Figure 1)

For  , we also assume that
, we also assume that  . Then for
. Then for  , the
, the  is the a layer between two parallel hyperplanes, and for
is the a layer between two parallel hyperplanes, and for  the boundary of the domain
the boundary of the domain  consists of two coaxial cylindrical surfaces. The intersections
consists of two coaxial cylindrical surfaces. The intersections  are precompact for all
are precompact for all  . Thus, the functions
. Thus, the functions  are exhaustion functions for
are exhaustion functions for  .
.
1.2. Structure Conditions
Let  be a subdomain of
be a subdomain of  and let
and let

be a vector function such that for a.e.  the function
the function

is defined and is continuous with respect to  . We assume that the function
. We assume that the function

is measurable in the Lebesgue sense for all  and
and

Suppose that for a.e.  and for all
and for all  the following properties hold:
the following properties hold:

with  and some constants
and some constants  . We consider the equation
. We consider the equation

An important special case of (1.17) is the Laplace equation

As in [4, Chapter 6], we call continuous weak solutions of (1.17)  -harmonic functions. However we should note that our definition of generalized solutions is slightly different from the definition given in [4, page 56].
-harmonic functions. However we should note that our definition of generalized solutions is slightly different from the definition given in [4, page 56].
1.3. Frequencies
Fix  and
and  . Let
. Let  be an open subset of
be an open subset of  (with respect to the relative topology of
(with respect to the relative topology of  ), and let
), and let  be a nonempty closed subset of
be a nonempty closed subset of  . We set
. We set

where  with
with  . If
. If  , then we call
, then we call  the first frequency of the order
the first frequency of the order  of the set
of the set  . If
. If  , then the quantity
, then the quantity  is thethird frequency.
is thethird frequency.
The second frequency is the following quantity:

where the supremum is taken over all constants  and
and  . See also Pólya and Szegö [5] as well as Lax [6].
. See also Pólya and Szegö [5] as well as Lax [6].
1.4. Generalized Boundary Conditions
Suppose that  is a proper subdomain of
is a proper subdomain of  . Let
. Let  be a locally Lipschitz function. We denote by
be a locally Lipschitz function. We denote by  the set of all points
the set of all points  at which
at which  does not have the differential. Let
does not have the differential. Let  be a subset and let
be a subset and let  be its boundary with respect to
be its boundary with respect to  . If
. If  is
is  -rectifiable, then it has locally finite perimeter in the sense of De Giorgi, and therefore a unit normal vector
-rectifiable, then it has locally finite perimeter in the sense of De Giorgi, and therefore a unit normal vector  exists
exists  -almost everywhere on
-almost everywhere on  [7, Sections 3.2.14, 3.2.15].
[7, Sections 3.2.14, 3.2.15].
Let  be a domain and let
be a domain and let  be a subset of the boundary of
be a subset of the boundary of  . Define the concept of a generalized solution of (1.17) with zero boundary conditions on
. Define the concept of a generalized solution of (1.17) with zero boundary conditions on  . A subset
. A subset  is called admissible, if
is called admissible, if  and
and  have a
have a  -rectifiable boundary with respect to
-rectifiable boundary with respect to  .
.
Suppose that  is unbounded. Let
is unbounded. Let  be a set closed in
be a set closed in  . We denote by
. We denote by  the collection of all subdomains
the collection of all subdomains  with
with  and
and  -rectifiable boundaries
-rectifiable boundaries  .
.
Definition 1.1.
We say that a locally Lipschitz function  is a generalized solution of (1.17) with the boundary condition
is a generalized solution of (1.17) with the boundary condition

if for every subdomain  ,
,

and for every locally Lipschitz function  the following property holds:
the following property holds:

Here  is the unit normal vector of
is the unit normal vector of  and
and  is the volume element on
is the volume element on  .
.
Definition 1.2.
We say that a locally Lipschitz function  is a generalized solution of (1.17) with the boundary condition
is a generalized solution of (1.17) with the boundary condition

if for every subdomain  with (1.22) and for every locally Lipschitz function
with (1.22) and for every locally Lipschitz function  the following property holds:
the following property holds:

In the case of a smooth boundary  , and
, and  , the relation (1.23) implies (1.17) with (1.21) everywhere on
, the relation (1.23) implies (1.17) with (1.21) everywhere on  . This requirement (1.25) implies (1.17) with (1.24) on
. This requirement (1.25) implies (1.17) with (1.24) on  . See [8, Section 9.2.1].
. See [8, Section 9.2.1].
The surface integrals exist by (1.22). Indeed, this assumption guarantees that  exists
exists  a.e. on
a.e. on  . The assumption that
. The assumption that  implies existence of a normal vector
implies existence of a normal vector  for
for  a.e. points on
a.e. points on  [7, Chapter 2, Section 3.2]. Thus, the scalar product
[7, Chapter 2, Section 3.2]. Thus, the scalar product  is defined and is finite a.e. on
is defined and is finite a.e. on  .
.
2. Saint-Venant's Principle
In this section, we will prove the Saint-Venant principle for solutions of the  -Laplace equation. The Saint-Venant principle states that strains in a body produced by application of a force onto a small part of its surface are of negligible magnitude at distances that are large compared to the diameter of the part where the force is applied. This well known result in elasticity theory is often stated and used in a loose form. For mathematical investigation of the results of this type, see, for example, [9].
-Laplace equation. The Saint-Venant principle states that strains in a body produced by application of a force onto a small part of its surface are of negligible magnitude at distances that are large compared to the diameter of the part where the force is applied. This well known result in elasticity theory is often stated and used in a loose form. For mathematical investigation of the results of this type, see, for example, [9].
In this paper the inequalities of the form (2.5), (2.4) are called the Saint-Venant principle (see also [9, 10]). Here we consider only the case of canonical domains. We plan to consider the general case in another article.
Let  . Fix a domain
. Fix a domain  in
in  with compact and smooth boundary, and write
with compact and smooth boundary, and write

We write  ,
,  , and
, and  . Let
. Let  ,
,  and
and

For  , we set
, we set

Theorem 2.1.
Let  , and let
, and let  . If
. If  is a generalized solution of (1.17) with the generalized boundary condition (1.21) on
is a generalized solution of (1.17) with the generalized boundary condition (1.21) on  , then the inequality
, then the inequality

holds for all  .
.
If  is a generalized solution of (1.17) with the generalized boundary condition (1.24), then
is a generalized solution of (1.17) with the generalized boundary condition (1.24), then

holds for all  . Here
. Here


Proof.
Case A.
At first we consider the case in which  is a generalized solution of (1.17) with the generalized boundary condition (1.24) on
is a generalized solution of (1.17) with the generalized boundary condition (1.24) on  . It is easy to see that a.e. on
. It is easy to see that a.e. on  ,
,

The domain  belongs to
belongs to  . Let
. Let  be a locally Lipschitz function. By (1.25) we have
be a locally Lipschitz function. By (1.25) we have

But

For  , we have by (1.16) and (1.25)
, we have by (1.16) and (1.25)

since  for
for  and
and  for
for  . We obtain
. We obtain

where

Note that we may also choose

to obtain an inequality similar to (2.12).
Next we will estimate the right side of (2.12). By (1.16) and the Hölder inequality,

By using (1.19), we may write


By (2.12) and the Fubini theorem,

By integrating this differential inequality, we have

for arbitrary  with
with  . We have shown that
. We have shown that

Case B.
Now we assume that  is a generalized solution of (1.17) with the boundary condition (1.21) on
is a generalized solution of (1.17) with the boundary condition (1.21) on  . Fix
. Fix  . By choosing
. By choosing  in (1.23), we see that
in (1.23), we see that

For an arbitrary constant  , we get from this and (1.23)
, we get from this and (1.23)

Thus

where

or

As above, we obtain

By using (1.20), we get

where  is the constant from (1.20). Then by (2.26) and (2.27),
is the constant from (1.20). Then by (2.26) and (2.27),

and by (2.25) we have

or

By integrating this inequality, we have shown that

3. Stagnation Zones
Next we apply the Saint-Venant principle to obtain information about stagnation zones of generalized solutions of (1.17). We first consider zones with respect to the Sobolev norm. Other results of this type follow immediately from well-known imbedding theorems.
3.1. Stagnation Zones with Respect to the 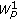 -Norm
-Norm
We rewrite (2.4) and (2.5) in another form. Let  and let
and let  . Fix a domain
. Fix a domain  in
in  with compact and smooth boundary, and write
with compact and smooth boundary, and write

We write

For  and
and

we have

and we denote

Let  . We write
. We write


Let  By (2.5) we have, for
By (2.5) we have, for  ,
,

where

By choosing the estimate as in (2.14), we also have

where

By adding these inequalities and noting that  , we obtain
, we obtain

Thus we have the estimate

Similarly, from (2.4) we obtain

From this we obtain the following theorem on stagnation  -zones.
-zones.
Theorem 3.1.
Let  ,
,  , and let
, and let  where
where  is as in (3.3). If
is as in (3.3). If  is a solution of (1.17) on
is a solution of (1.17) on  with the generalized boundary condition (1.21) on
with the generalized boundary condition (1.21) on  , where
, where  and
and

or a solution of (1.17) on  with the generalized boundary condition (1.24) on
with the generalized boundary condition (1.24) on  and
and

then the subdomain  is an
is an  -zone with respect to the
-zone with respect to the  -norm, that is,
-norm, that is,

where  is as in (3.6).
is as in (3.6).
3.2. Stagnation Zones with Respect to the 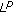 -Norm
-Norm
Let  , and let
, and let  where
where  is as in (3.3).
is as in (3.3).
Denote by  the best constant of the imbedding theorem from
the best constant of the imbedding theorem from  to
to  that is in the inequality
that is in the inequality

if such constant exists (see Maz'ya [11] or [12]). Then we obtain from (3.13), (3.14)


These relations can be used to obtain information about stagnation zones with respect to the  -norm. Namely, we have the following.
-norm. Namely, we have the following.
Theorem 3.2.
Let  , and let
, and let

where  is a domain in
is a domain in  with compact and smooth boundary. If
with compact and smooth boundary. If  is a solution of (1.17) on
is a solution of (1.17) on  , with the generalized boundary condition, (1.21) or (1.24), on
, with the generalized boundary condition, (1.21) or (1.24), on  , where
, where  , and the right side of, (3.19) or (3.20), is smaller than
, and the right side of, (3.19) or (3.20), is smaller than  , then the domain
, then the domain  is a stagnation zone with the deviation
is a stagnation zone with the deviation  in the sense of the
in the sense of the  -norm on
-norm on  .
.
3.3. Stagnation Zones for Bounded, Uniformly Continuous Functions
Let  , and let
, and let  where
where  is as in (3.3).
is as in (3.3).
As before, denote by  the best constant of the imbedding theorem from
the best constant of the imbedding theorem from  to
to  , that is in the inequality
, that is in the inequality

if such constant exists. For example, if the domain  is convex, then (3.22) holds for
is convex, then (3.22) holds for  (see Maz'ya [11] or [12, page 85]).
(see Maz'ya [11] or [12, page 85]).
In this case from (3.13), (3.14), we obtain


These relations can be used to obtain theorems about stagnation zones for bounded, uniformly continuous functions.
Theorem 3.3.
Let  . If
. If  is a solution of (1.17),
is a solution of (1.17),  , on
, on  where
where  is as before with the generalized boundary condition, (1.21) or (1.24), on
is as before with the generalized boundary condition, (1.21) or (1.24), on  where
where  and the right side of, (3.23) or (3.24), is smaller than
and the right side of, (3.23) or (3.24), is smaller than  , then the domain
, then the domain  is a stagnation zone with the deviation
is a stagnation zone with the deviation  in the sense of the norm
in the sense of the norm  .
.
4. Other Applications
Next we prove Phragmén-Lindelöf type theorems for the solutions of the  -Laplace equation with boundary conditions (1.21) and (1.24).
-Laplace equation with boundary conditions (1.21) and (1.24).
4.1. Estimates for 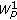 -Norms
-Norms
Let  , and let
, and let  be a domain in
be a domain in  with compact and smooth boundary. Write
with compact and smooth boundary. Write

Suppose that  is as in (3.3). First we will prove some estimates of the
is as in (3.3). First we will prove some estimates of the  -norm of a solution. Let
-norm of a solution. Let  be a solution of (1.17) on
be a solution of (1.17) on  with the generalized boundary condition (1.21) on
with the generalized boundary condition (1.21) on  . Fix
. Fix  and estimate
and estimate  .
.
Let  be a Lipschitz function such that
be a Lipschitz function such that

We choose

The function  is admissible in Definition 1.1 for
is admissible in Definition 1.1 for

As in (2.22), we may by (1.23) write

By the construction of  , (4.2), and (4.3), the surface integral is equal to zero, and we have
, (4.2), and (4.3), the surface integral is equal to zero, and we have

Thus by (1.16),

Now we note that

and by the Hölder inequality,

From this inequality and (4.7), we obtain

Because  on
on  , we have the following inequality:
, we have the following inequality:

Next we will find that

where the minimum is taken over all  in (4.3). We have
in (4.3). We have


Because by the Hölder inequality

we have

and hence,

It is easy to see that here the equality holds for a special choice of  . Thus
. Thus

Similarly,

From (4.14) we obtain

By using (4.11), we obtain the inequality

where  is an arbitrary constant. From this we obtain
is an arbitrary constant. From this we obtain

where  .
.
Similarly, for the solutions of the  -Laplace equation with the boundary condition (1.24), we may prove that
-Laplace equation with the boundary condition (1.24), we may prove that

It follows that

4.2. Phragmén-Lindelöf Type Theorems I
We prove Phragmén-Lindelöf type theorems for cylindrical domains. Let  . Fix a domain
. Fix a domain  in
in  with compact and smooth boundary. Consider the domain
with compact and smooth boundary. Consider the domain

Let  be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.21) on
be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.21) on  .
.
Fix  , and let
, and let  be as in (3.3). Let
be as in (3.3). Let  , where
, where  is the
is the  th unit coordinate vector, and let
th unit coordinate vector, and let  By (4.22)
By (4.22)

By using (3.14), we obtain from this the inequality

We observe that in this case

and hence,

It follows that

By letting  , we obtain the following statement.
, we obtain the following statement.
Theorem 4.1.
Fix a domain  in
in  with compact and smooth boundary. Let
with compact and smooth boundary. Let

and let  be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.21) on
be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.21) on  . If for a constant
. If for a constant  the right side of (4.30) goes to
the right side of (4.30) goes to  as
as  , then
, then  on
on  .
.
Similarly for a solution  of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.24), we may write
of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.24), we may write

However here we do not have any identity similar to (4.28). We have the following.
Theorem 4.2.
Fix a domain  in
in  with compact and smooth boundary. Let
with compact and smooth boundary. Let

and let  be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.24) on
be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.24) on  . If the right side of (4.32) tends to
. If the right side of (4.32) tends to  as
as  , then
, then  on
on  .
.
If  everywhere on
everywhere on  , then an identity similar to (4.28) holds in the following form:
, then an identity similar to (4.28) holds in the following form:

As above, we find that

Thus we obtain the following.
Corollary 4.3.
Fix a domain  in
in  with compact and smooth boundary. Let
with compact and smooth boundary. Let

and let  be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition
be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition  on
on  . If the right side of (4.35) tends to
. If the right side of (4.35) tends to  as
as  , then
, then  on
on  .
.
4.3. Phragmén-Lindelöf Type Theorems II
We prove Phragmén-Lindelöf type theorems for canonical domains of an arbitrary form. Let  . We consider a domain
. We consider a domain

where  is a domain in
is a domain in  with compact and smooth boundary. Let
with compact and smooth boundary. Let  be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.21) on
be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.21) on  .
.
Fix  . Let
. Let  By (4.22) we may write
By (4.22) we may write

where  . As in (3.14), we obtain from (2.4) the estimate
. As in (3.14), we obtain from (2.4) the estimate

By combining these inequalities, we obtain

The inequality (4.40) holds for arbitrary constant  and every
and every  . Thus the following statement holds.
. Thus the following statement holds.
Theorem 4.4.
Let  be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.21) on
be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.21) on  ,
,  . If for a constant
. If for a constant  the right side of (4.40) tends to
the right side of (4.40) tends to  as
as  , then
, then  on
on  .
.
If  satisfies (1.17) with (1.15), (1.16) and the boundary condition (1.24) on
satisfies (1.17) with (1.15), (1.16) and the boundary condition (1.24) on  , then we have
, then we have

We obtain the following.
Theorem 4.5.
Fix a domain  in
in  , where
, where  , with compact and smooth boundary. Let
, with compact and smooth boundary. Let

and let  be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.24) on
be a generalized solution of (1.17) with (1.15) and (1.16) satisfying the boundary condition (1.24) on  . If for a constant
. If for a constant  the right side of (4.41) tends to
the right side of (4.41) tends to  as
as  , then
, then  on
on  .
.
References
Miklyukov VM (Ed): Proceedings of the Seminar 'Superslow Processes'. Issue 1, Volgograd State University, Volgograd, Russia; 2006.
Miklyukov VM (Ed): Proceedings of the Seminar 'Superslow Processes'. Issue 2, Volgograd State University, Volgograd, Russia; 2007.
Miklyukov VM:Stagnation zones of
 -solutions, Memory I.N. Vekua. Georgian Mathematical Journal 2007, 14(3):519-531.
-solutions, Memory I.N. Vekua. Georgian Mathematical Journal 2007, 14(3):519-531.Heinonen J, Kilpeläinen T, Martio O: Nonlinear Potential Theory of Degenerate Elliptic Equations, Oxford Mathematical Monographs. The Clarendon Press, Oxford, UK; 1993:vi+363.
Pólya G, Szegö G: Isoperimetric Inequalities in Mathematical Physics. Princeton University Press, Princeton, NJ, USA; 1951:xvi+279.
Lax PD: A Phragmén-Lindelöf theorem in harmonic analysis and its application to some questions in the theory of elliptic equations. Communications on Pure and Applied Mathematics 1957, 10: 361-389. 10.1002/cpa.3160100305
Federer H: Geometric Measure Theory, Die Grundlehren der mathematischen Wissenschaften. Volume 153. Springer, New York, NY, USA; 1969:xiv+676.
Miklyukov VM: Introduction to Nonsmooth Analysis. 2nd edition. Izd-vo VolGU, Volgograd, Russia; 2008.
Barbarosie C, Toader A-M: Saint-Venant's principle and its connections to shape and topology optimization. Zeitschrift für Angewandte Mathematik und Mechanik 2008, 88(1):23-32. 10.1002/zamm.200710357
Oleĭnik OA, Yosifian GA: Boundary value problems for second order elliptic equations in unbounded domains and Saint-Venant's principle. Annali della Scuola Normale Superiore, Classe di Scienze 1977, 4(4):269-290.
Maz'ya VG: Sobolev Spaces, Springer Series in Soviet Mathematics. Springer, Berlin, Germany; 1985:xix+486.
Adams R, Fournier J: Sobolev Spaces, Pure and Applied Mathematics. Volume 140. 2nd edition. Academic Press, New York, NY, USA; 2003:xiv+305.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Miklyukov, V., Rasila, A. & Vuorinen, M. Stagnation Zones for 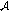 -Harmonic Functions on Canonical Domains.
Bound Value Probl 2009, 853607 (2010). https://doi.org/10.1155/2009/853607
-Harmonic Functions on Canonical Domains.
Bound Value Probl 2009, 853607 (2010). https://doi.org/10.1155/2009/853607
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/853607

 (a) and
(a) and  in
in  .
.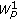 -Norm
-Norm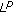 -Norm
-Norm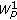 -Norms
-Norms -solutions, Memory I.N. Vekua. Georgian Mathematical Journal 2007, 14(3):519-531.
-solutions, Memory I.N. Vekua. Georgian Mathematical Journal 2007, 14(3):519-531.