- Research Article
- Open access
- Published:
Positive Solutions to Singular and Delay Higher-Order Differential Equations on Time Scales
Boundary Value Problems volume 2009, Article number: 937064 (2009)
Abstract
We are concerned with singular three-point boundary value problems for delay higher-order dynamic equations on time scales. Theorems on the existence of positive solutions are obtained by utilizing the fixed point theorem of cone expansion and compression type. An example is given to illustrate our main result.
1. Introduction
In this paper, we are concerned with the following singular three-point boundary value problem (BVP for short) for delay higher-order dynamic equations on time scales:

where  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  . The functional
. The functional  is continuous and
is continuous and  is continuous. Our nonlinearity
is continuous. Our nonlinearity  may have singularity at
may have singularity at  and/or
and/or  and
and  may have singularity at
may have singularity at  .
.
To understand the notations used in (1.1), we recall the following definitions which can be found in [1, 2].
(a) A time scale  is a nonempty closed subset of the real numbers
is a nonempty closed subset of the real numbers  .
.  has the topology that it inherits from the real numbers with the standard topology. It follows that the jump operators
has the topology that it inherits from the real numbers with the standard topology. It follows that the jump operators  ,
,

(supplemented by  and
and  ) are well defined. The point
) are well defined. The point  is left-dense, left-scattered, right-dense, right-scattered if
is left-dense, left-scattered, right-dense, right-scattered if  ,
,  ,
,  ,
,  , respectively. If
, respectively. If  has a left-scattered maximum
has a left-scattered maximum  (right-scattered minimum
(right-scattered minimum  ), define
), define  (
( ); otherwise, set
); otherwise, set  (
( ). By an interval
). By an interval  we always mean the intersection of the real interval
we always mean the intersection of the real interval  with the given time scale, that is,
with the given time scale, that is,  . Other types of intervals are defined similarly.
. Other types of intervals are defined similarly.
(b) For a function  and
and  , the
, the  -derivative of
-derivative of  at
at  , denoted by
, denoted by  , is the number (provided it exists) with the property that, given any
, is the number (provided it exists) with the property that, given any  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

(c) For a function  and
and  , the
, the  -derivative of
-derivative of  at
at  , denoted by
, denoted by  , is the number (provided it exists) with the property that, given any
, is the number (provided it exists) with the property that, given any  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

(d) If 
 then we define the integral
then we define the integral

Theoretically, dynamic equations on time scales can build bridges between continuous and discrete mathematics. Practically, dynamic equations have been proposed as models in the study of insect population models, neural networks, and many physical phenomena which include gas diffusion through porous media, nonlinear diffusion generated by nonlinear sources, chemically reacting systems as well as concentration in chemical of biological problems [2]. Hence, two-point and multipoint boundary value problems for dynamic equations on time scales have attracted many researchers' attention (see, e.g., [1–19] and references therein). Moreover, singular boundary value problems have also been treated in many papers (see, e.g., [4, 5, 12–14, 18] and references therein).
In 2004, J. J. DaCunha et al. [13] considered singular second-order three-point boundary value problems on time scales

and obtained the existence of positive solutions by using a fixed point theorem due to Gatica et al. [14], where  is decreasing in
is decreasing in  for every
for every  and may have singularity at
and may have singularity at  .
.
In 2006, Boey and Wong [11] were concerned with higher-order differential equation on time scales of the form

where  are fixed integers satisfying
are fixed integers satisfying  ,
,  . They obtained some existence theorems of positive solutions by using Krasnosel'skii fixed point theorem.
. They obtained some existence theorems of positive solutions by using Krasnosel'skii fixed point theorem.
Recently, Anderson and Karaca [8] studied higher-order three-point boundary value problems on time scales and obtained criteria for the existence of positive solutions.
The purpose of this paper is to investigate further the singular BVP for delay higher-order dynamic equation (1.1). By the use of the fixed point theorem of cone expansion and compression type, results on the existence of positive solutions to the BVP (1.1) are established.
The paper is organized as follows. In Section 2, we give some lemmas, which will be required in the proof of our main theorem. In Section 3, we prove some theorems on the existence of positive solutions for BVP (1.1). Moreover, we give an example to illustrate our main result.
2. Lemmas
For  , let
, let  be Green's function of the following three-point boundary value problem:
be Green's function of the following three-point boundary value problem:

where  and
and  satisfy the following condition:
satisfy the following condition:
-
(C)
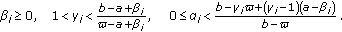 (2.2)
(2.2)
Throughout the paper, we assume that  .
.
From [8], we know that for any  and
and  ,
,

where

The following four lemmas can be found in [8].
Lemma 2.1.
Suppose that the condition (C) holds. Then the Green function of  in (2.3) satisfies
in (2.3) satisfies

Lemma 2.2.
Assume that the condition (C) holds. Then Green's function  in (2.3) satisfies
in (2.3) satisfies

Remark 2.3.
 If
If 
 , we know that
, we know that  is nonincreasing in
is nonincreasing in  and
and

Therefore, we have

where

 If
If  and
and  satisfy the other cases, then we get that
satisfy the other cases, then we get that  is nondecreasing in
is nondecreasing in  and
and

Lemma 2.4.
Assume that (C) holds. Then Green's function  in (2.3) verifies the following inequality:
in (2.3) verifies the following inequality:

Remark 2.5.
If 
 , then we find
, then we find

So there exists a misprint on [8, Page 2431, line 23]. From (2.3), it follows that

Consequently, we get

If  ,
,  , then, from (2.8), we obtain
, then, from (2.8), we obtain

Remark 2.6.
If we set  , then we have
, then we have

Denote

Thus we have

Lemma 2.7.
Assume that condition (C) is satisfied. For  as in (2.3), put
as in (2.3), put  and recursively define
and recursively define

for  . Then
. Then  is Green's function for the homogeneous problem
is Green's function for the homogeneous problem

Lemma 2.8.
Assume that (C) holds. Denote

then Green's function  in Lemma 2.7 satisfies
in Lemma 2.7 satisfies

where

Proof.
We proceed by induction on  . We denote the statement by
. We denote the statement by  . From Lemma 2.7, it follows that
. From Lemma 2.7, it follows that

and from (2.18), we have

So  is true.
is true.
We now assume that  is true for some positive integer
is true for some positive integer  . From Lemma 2.7, it follows that
. From Lemma 2.7, it follows that

So  holds. Thus
holds. Thus  is true by induction.
is true by induction.
Lemma 2.9 (see [20]).
Let  be a real Banach space and
be a real Banach space and  a cone. Assume that
a cone. Assume that  is completely continuous operator such that
is completely continuous operator such that
(i)  for
for  and
and  for
for  ,
,
(ii)  for
for  and
and  for
for  .
.
Then  has a fixed point
has a fixed point  with
with  .
.
3. Main Results
We assume that  and
and  are strictly decreasing and strictly increasing sequences, respectively, with
are strictly decreasing and strictly increasing sequences, respectively, with  ,
,  and
and  . A Banach space
. A Banach space  is the set of real-valued continuous (in the topology of
is the set of real-valued continuous (in the topology of  ) functions
) functions  defined on
defined on  with the norm
with the norm

Define a cone by

Set

Assume that
(C1)  is continuous;
is continuous;
(C2) we have

for constants  and
and  with
with  ;
;
(C3) the function  is continuous and
is continuous and  is continuous satisfying
is continuous satisfying

We seek positive solutions  , satisfying (1.1). For this end, we transform (1.1) into an integral equation involving the appropriate Green function and seek fixed points of the following integral operator.
, satisfying (1.1). For this end, we transform (1.1) into an integral equation involving the appropriate Green function and seek fixed points of the following integral operator.
Define an operator  by
by

where  .
.
Proposition 3.1.
Let (C1), (C2), and (C3) hold, and let  ,
,  be fixed constants with
be fixed constants with  . Then
. Then  is completely continuous.
is completely continuous.
Proof.
We separate the proof into four steps.
Step 1.
For each  ,
,  is bounded.
is bounded.
By condition (C3), there exists some positive integer  satisfying
satisfying

where

here, we used the fact that for each  and
and  ,
,

where

Set

Then we obtain

Consequently,  is bounded and well defined.
is bounded and well defined.
Step 2.
 . For every
. For every  , we get from (2.22)
, we get from (2.22)

Then by the above inequality

This leads to  .
.
Step 3.
We will show that  is continuous. Let
is continuous. Let  be any sequence in
be any sequence in  such that
such that  . Notice also that as
. Notice also that as  ,
,

Now these together with (C2) and the Lebesgue dominated convergence theorem [10] yield that as  ,
,

Step 4.
 is compact.
is compact.
Define

and an operator sequence  for a fixed
for a fixed  by
by

Clearly, the operator sequence  is compact by using the Arzela-Ascoli theorem [3], for each
is compact by using the Arzela-Ascoli theorem [3], for each  . We will prove that
. We will prove that  converges uniformly to
converges uniformly to  on
on  . For any
. For any  , we obtain
, we obtain

From (C1), (C2), and the Lebesgue dominated convergence theorem [10], we see that the right-hand side (3.19) can be sufficiently small for  beingbig enough. Hence the sequence
beingbig enough. Hence the sequence  of compact operators converges uniformly to
of compact operators converges uniformly to  on
on  so that operator
so that operator  is compact. Consequently,
is compact. Consequently,  is completely continuous by using the Arzela-Ascoli theorem [3].
is completely continuous by using the Arzela-Ascoli theorem [3].
Proposition 3.2.
It holds that  is a solution of (1.1) if and only if
is a solution of (1.1) if and only if  .
.
Proof.
If  and
and  , then we have
, then we have

and for any  ,
,

From [8, Lemma 3.1], we know that  on
on  . So we conclude that
. So we conclude that  is the solution of BVP (1.1).
is the solution of BVP (1.1).
For convenience, we list the following notations and assumptions:




From condition (C2) and (3.12), we have  .
.
Theorem 3.3.
Assume that there exist positive constants  with
with  ,
,  and
and  such that
such that
(i)  and
and  ;
;
(ii)  , for all
, for all  and
and  .
.
If (C1), (C2), and (C3) hold, then the boundary value problem (1.1) has at least one positive solution  such that
such that

Proof.
Define the operator  by (3.6). From (i) and (3.23), it follows that there exists
by (3.6). From (i) and (3.23), it follows that there exists  such that
such that

We claim that

If it is false, then there exists some  with
with  , that is,
, that is,  which implies that
which implies that  for
for  .
.
Set

We know from (2.22) and (3.27) that for  ,
,

the first inequality of (C2) implies that

Clearly, (3.31) contradicts (3.29). This means that (3.28) holds.
Next we will show that

Suppose on the contrary that there exists some  with
with  for all
for all  .
.
For  , from (i) and (3.24), there exists
, from (i) and (3.24), there exists  such that
such that

and for  , there exists
, there exists  , from (ii), such that
, from (ii), such that

Put

If  , then we take
, then we take  . It is easy to see that
. It is easy to see that  for
for  and
and  ,
,  , that is,
, that is,  . From (3.33) and (3.34), we find that
. From (3.33) and (3.34), we find that

yielding a contradiction with  for all
for all  . This means that (3.32) holds. Therefore, from (3.28), (3.32) and Lemma 2.9, we conclude that the operator
. This means that (3.32) holds. Therefore, from (3.28), (3.32) and Lemma 2.9, we conclude that the operator  has at least one fixed point
has at least one fixed point  . From the definition of the cone
. From the definition of the cone  and (2.18), we see that
and (2.18), we see that  for all
for all  . Thus, Proposition 3.2 implies that
. Thus, Proposition 3.2 implies that  is a solution of BVP (1.1). So we obtain the desired result.
is a solution of BVP (1.1). So we obtain the desired result.
Adopting the same argument as in Theorem 3.3, we obtain the following results.
Corollary 3.4.
Let  be as in Theorem 3.3.Suppose that (ii) of Theorem 3.3 holds and
be as in Theorem 3.3.Suppose that (ii) of Theorem 3.3 holds and  . If (C1), (C2), and (C3) holds, then boundary value problem (1.1) has at least one positive solution
. If (C1), (C2), and (C3) holds, then boundary value problem (1.1) has at least one positive solution  such that
such that

Theorem 3.5.
Assume that there exist positive constants  with
with  ,
,  and
and  ,
,  such that
such that
(iii)  and
and 
(iv)  , for all
, for all  and
and  .
.
If (C1), (C2), and (C3) hold, then boundary value problem (1.1) has at least  positive solutions
positive solutions  such that for
such that for 

Example 3.6.
Let  . Consider the following singular three-point boundary value problems for delay four-order dynamic equations:
. Consider the following singular three-point boundary value problems for delay four-order dynamic equations:

where, for any  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  ,
,

Clearly, we know that

Simple computations yield

Obviously,

If  , then we have
, then we have

Therefore, we get

From (3.25), it follows that

Thus,

Therefore, by Theorem 3.3, the BVP (3.39) has at least one positive solution  such that
such that

References
Atici FM, Guseinov GSh: On Green's functions and positive solutions for boundary value problems on time scales. Journal of Computational and Applied Mathematics 2002, 141(1-2):75-99. 10.1016/S0377-0427(01)00437-X
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Application. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Agarwal RP, Bohner M, Rehák P: Half-linear dynamic equations. In Nonlinear Analysis and Applications: To V. Lakshmikantham on His 80th Birthday. Vol. 1, 2. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:1-57.
Agarwal RP, Otero-Espinar V, Perera K, Vivero DR: Multiple positive solutions of singular Dirichlet problems on time scales via variational methods. Nonlinear Analysis: Theory, Methods & Applications 2007, 67(2):368-381. 10.1016/j.na.2006.05.014
Agarwal RP, Otero-Espinar V, Perera K, Vivero DR: Multiple positive solutions in the sense of distributions of singular BVPs on time scales and an application to Emden-Fowler equations. Advances in Difference Equations 2008, 2008:-13.
Ahmad B, Nieto JJ:The monotone iterative technique for three-point second-order integrodifferential boundary value problems with
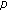 -Laplacian. Boundary Value Problems 2007, 2007:-9.
-Laplacian. Boundary Value Problems 2007, 2007:-9.Anderson DR: Solutions to second-order three-point problems on time scales. Journal of Difference Equations and Applications 2002, 8(8):673-688. 10.1080/1023619021000000717
Anderson DR, Karaca IY: Higher-order three-point boundary value problem on time scales. Computers & Mathematics with Applications 2008, 56(9):2429-2443. 10.1016/j.camwa.2008.05.018
Anderson DR, Smyrlis G: Solvability for a third-order three-point BVP on time scales. Mathematical and Computer Modelling 2009, 49(9-10):1994-2001. 10.1016/j.mcm.2008.11.009
Aulbach B, Neidhart L: Integration on measure chains. In Proceedings of the 6th International Conference on Difference Equations, 2004, Boca Raton, Fla, USA. CRC Press; 239-252.
Boey KL, Wong PJY: Positive solutions of two-point right focal boundary value problems on time scales. Computers & Mathematics with Applications 2006, 52(3-4):555-576. 10.1016/j.camwa.2006.08.025
Cabada A, Cid JÁ: Existence of a solution for a singular differential equation with nonlinear functional boundary conditions. Glasgow Mathematical Journal 2007, 49(2):213-224. 10.1017/S0017089507003679
DaCunha JJ, Davis JM, Singh PK: Existence results for singular three point boundary value problems on time scales. Journal of Mathematical Analysis and Applications 2004, 295(2):378-391. 10.1016/j.jmaa.2004.02.049
Gatica JA, Oliker V, Waltman P: Singular nonlinear boundary value problems for second-order ordinary differential equations. Journal of Differential Equations 1989, 79(1):62-78. 10.1016/0022-0396(89)90113-7
Henderson J, Tisdell CC, Yin WKC: Uniqueness implies existence for three-point boundary value problems for dynamic equations. Applied Mathematics Letters 2004, 17(12):1391-1395. 10.1016/j.am1.2003.08.015
Kaufmann ER, Raffoul YN: Positive solutions for a nonlinear functional dynamic equation on a time scale. Nonlinear Analysis: Theory, Methods & Applications 2005, 62(7):1267-1276. 10.1016/j.na.2005.04.031
Khan RA, Nieto JJ, Otero-Espinar V: Existence and approximation of solution of three-point boundary value problems on time scales. Journal of Difference Equations and Applications 2008, 14(7):723-736. 10.1080/10236190701840906
Liang J, Xiao T-J, Hao Z-C: Positive solutions of singular differential equations on measure chains. Computers & Mathematics with Applications 2005, 49(5-6):651-663. 10.1016/j.camwa.2004.12.001
Yaslan İ: Multiple positive solutions for nonlinear three-point boundary value problems on time scales. Computers & Mathematics with Applications 2008, 55(8):1861-1869. 10.1016/j.camwa.2007.07.005
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Acknowledgments
The authors would like to thank the referees for helpful comments and suggestions. The work was supported partly by the NSF of China (10771202), the Research Fund for Shanghai Key Laboratory of Modern Applied Mathematics (08DZ2271900), and the Specialized Research Fund for the Doctoral Program of Higher Education of China (2007035805).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hu, LG., Xiao, TJ. & Liang, J. Positive Solutions to Singular and Delay Higher-Order Differential Equations on Time Scales. Bound Value Probl 2009, 937064 (2009). https://doi.org/10.1155/2009/937064
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/937064
 -Laplacian. Boundary Value Problems 2007, 2007:-9.
-Laplacian. Boundary Value Problems 2007, 2007:-9.