- Research Article
- Open access
- Published:
Unbounded Solutions of Second-Order Multipoint Boundary Value Problem on the Half-Line
Boundary Value Problems volume 2010, Article number: 236560 (2010)
Abstract
This paper investigates the second-order multipoint boundary value problem on the half-line  ,
, ,
,  ,
,  ,
,  , where
, where  ,
,  ,
,  ,
,  , and
, and  is continuous. We establish sufficient conditions to guarantee the existence of unbounded solution in a special function space by using nonlinear alternative of Leray-Schauder type. Under the condition that
is continuous. We establish sufficient conditions to guarantee the existence of unbounded solution in a special function space by using nonlinear alternative of Leray-Schauder type. Under the condition that  is nonnegative, the existence and uniqueness of unbounded positive solution are obtained based upon the fixed point index theory and Banach contraction mapping principle. Examples are also given to illustrate the main results.
is nonnegative, the existence and uniqueness of unbounded positive solution are obtained based upon the fixed point index theory and Banach contraction mapping principle. Examples are also given to illustrate the main results.
1. Introduction
In this paper, we consider the following second-order multipoint boundary value problem on the half-line

where  , and
, and  is continuous, in which
is continuous, in which  .
.
The study of multipoint boundary value problems (BVPs) for second-order differential equations was initiated by Bicadze and Samarskĭ [1] and later continued by II'in and Moiseev [2, 3] and Gupta [4]. Since then, great efforts have been devoted to nonlinear multi-point BVPs due to their theoretical challenge and great application potential. Many results on the existence of (positive) solutions for multi-point BVPs have been obtained, and for more details the reader is referred to [5–10] and the references therein. The BVPs on the half-line arise naturally in the study of radial solutions of nonlinear elliptic equations and models of gas pressure in a semi-infinite porous medium [11–13] and have been also widely studied [14–27]. When  , BVP (1.1) reduces to the following three-point BVP on the half-line:
, BVP (1.1) reduces to the following three-point BVP on the half-line:

where  . Lian and Ge [16] only studied the solvability of BVP (1.2) by the Leray-Schauder continuation theorem. When
. Lian and Ge [16] only studied the solvability of BVP (1.2) by the Leray-Schauder continuation theorem. When  ,
,  , and nonlinearity
, and nonlinearity  is variable separable, BVP (1.1) reduces to the second order two-point BVP on the half-line
is variable separable, BVP (1.1) reduces to the second order two-point BVP on the half-line

Yan et al. [17] established the results of existence and multiplicity of positive solutions to the BVP (1.3) by using lower and upper solutions technique.
Motivated by the above works, we will study the existence results of unbounded (positive) solution for second order multi-point BVP (1.1). Our main features are as follows. Firstly, BVP (1.1) depends on derivative, and the boundary conditions are more general. Secondly, we will study multi-point BVP on infinite intervals. Thirdly, we will obtain the unbounded (positive) solution to BVP (1.1). Obviously, with the boundary condition in (1.1), if the solution exists, it is unbounded. Hence, we extend and generalize the results of [16, 17] to some degree. The main tools used in this paper are Leray-Schauder nonlinear alternative and the fixed point index theory.
The rest of the paper is organized as follows. In Section 2, we give some preliminaries and lemmas. In Section 3, the existence of unbounded solution is established. In Section 4, the existence and uniqueness of positive solution are obtained. Finally, we formulate two examples to illustrate the main results.
2. Preliminaries and Lemmas
Denote  , where
, where  . Let
. Let

For any  , define
, define

then  is a Banach space with the norm
is a Banach space with the norm  (see [17]).
(see [17]).
The Arzela-Ascoli theorem fails to work in the Banach space  due to the fact that the infinite interval
due to the fact that the infinite interval  is noncompact. The following compactness criterion will help us to resolve this problem.
is noncompact. The following compactness criterion will help us to resolve this problem.
Lemma 2.1 (see [17]).
Let  . Then,
. Then,  is relatively compact in
is relatively compact in  if the following conditions hold:
if the following conditions hold:
(a)  is bounded in
is bounded in  ;
;
(b) the functions belonging to  and
and  are locally equicontinuous on
are locally equicontinuous on  ;
;
(c) the functions from  and
and  are equiconvergent, at
are equiconvergent, at  .
.
Throughout the paper we assume the following.
Suppose that  , and there exist nonnegative functions
, and there exist nonnegative functions  with
with  such that
such that


 , where
, where

Denote

Lemma 2.2.
Supposing that  with
with  , then BVP
, then BVP

has a unique solution

where

in which  , and
, and  for
for  .
.
Proof.
Integrating the differential equation from  to
to  , one has
, one has

Then, integrating the above integral equation from  to
to  , noticing that
, noticing that  and
and  , we have
, we have

Since  , it holds that
, it holds that

By using arguments similar to those used to prove Lemma 2.2 in [9], we conclude that (2.7) holds. This completes the proof.
Now, BVP (1.1) is equivalent to

Letting  , (2.12) becomes
, (2.12) becomes

For  , define operator
, define operator  by
by

Then,

Set

Remark 2.3.
 is the Green function for the following associated homogeneous BVP on the half-line:
is the Green function for the following associated homogeneous BVP on the half-line:

It is not difficult to testify that

Let us first give the following result of completely continuous operator.
Lemma 2.4.
Supposing that  and
and  hold, then
hold, then  is completely continuous.
is completely continuous.
Proof.
-
(1)
First, we show that
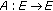 is well defined.
is well defined.
For any  , there exists
, there exists  such that
such that  . Then,
. Then,

so

Similarly,


Further,


On the other hand, for any  and
and  , by Remark 2.3, we have
, by Remark 2.3, we have

Hence, by  , the Lebesgue dominated convergence theorem, and the continuity of
, the Lebesgue dominated convergence theorem, and the continuity of  , for any
, for any  , we have
, we have

So,  for any
for any  .
.
We can show that  . In fact, by (2.23) and (2.24), we obtain
. In fact, by (2.23) and (2.24), we obtain

Hence,  is well defined.
is well defined.
-
(2)
We show that
 is continuous.
is continuous.
Suppose  , and
, and  . Then,
. Then,  as
as  , and there exists
, and there exists  such that
such that  . The continuity of
. The continuity of  implies that
implies that

as  . Moreover, since
. Moreover, since

we have from the Lebesgue dominated convergence theorem that

Thus,  is continuous.
is continuous.
-
(3)
We show that
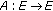 is relatively compact.
is relatively compact.
(a) Let  be a bounded subset. Then, there exists
be a bounded subset. Then, there exists  such that
such that  for all
for all  . By the similar proof of (2.20) and (2.22), if
. By the similar proof of (2.20) and (2.22), if  , one has
, one has

which implies that  is uniformly bounded.
is uniformly bounded.
(b) For any  , if
, if  , we have
, we have

Thus, for any  there exists
there exists  such that if
such that if  , then
, then

Since  is arbitrary, then
is arbitrary, then  and
and  are locally equicontinuous on
are locally equicontinuous on  .
.
(c) For  , from (2.27), we have
, from (2.27), we have

which means that  and
and  are equiconvergent at
are equiconvergent at  . By Lemma 2.1,
. By Lemma 2.1,  is relatively compact.
is relatively compact.
Therefore,  is completely continuous. The proof is complete.
is completely continuous. The proof is complete.
Let  be Banach space,
be Banach space,  be a bounded open subset of
be a bounded open subset of  , and
, and  be a completely continuous operator. Then either there exist
be a completely continuous operator. Then either there exist  such that
such that  , or there exists a fixed point
, or there exists a fixed point  .
.
Let  be a bounded open set in real Banach space
be a bounded open set in real Banach space  , let
, let  be a cone of
be a cone of  , and let
, and let  be completely continuous. Suppose that
be completely continuous. Suppose that

Then,

3. Existence Result
In this section, we present the existence of an unbounded solution for BVP (1.1) by using the Leray-Schauder nonlinear alternative.
Theorem 3.1.
Suppose that conditions  hold. Then BVP (1.1) has at least one unbounded solution.
hold. Then BVP (1.1) has at least one unbounded solution.
Proof.
Since  , by
, by  , we have
, we have  , a.e.
, a.e.  , which implies that
, which implies that  . Set
. Set

From Lemmas 2.2 and 2.4, BVP (1.1) has a solution  if and only if
if and only if  is a fixed point of
is a fixed point of  in
in  . So, we only need to seek a fixed point of
. So, we only need to seek a fixed point of  in
in  .
.
Suppose  such that
such that  . Then
. Then

Therefore,

which contradicts  . By Lemma 2.5,
. By Lemma 2.5,  has a fixed point
has a fixed point  . Letting
. Letting  , boundary conditions imply that
, boundary conditions imply that  is an unbounded solution of BVP (1.1).
is an unbounded solution of BVP (1.1).
4. Existence and Uniqueness of Positive Solution
In this section, we restrict the nonlinearity  and discuss the existence and uniqueness of positive solution for BVP (1.1).
and discuss the existence and uniqueness of positive solution for BVP (1.1).
Define the cone  as follows:
as follows:

Lemma 4.1.
Suppose that  and
and  hold. Then,
hold. Then,  is completely continuous.
is completely continuous.
Proof.
Lemma 2.4 shows that  is completely continuous, so we only need to prove
is completely continuous, so we only need to prove  . Since
. Since  , and from Remark 2.3, we have
, and from Remark 2.3, we have

Then,

Therefore,  .
.
Theorem 4.2.
Suppose that conditions  and
and  hold and the following condition holds:
hold and the following condition holds:
suppose that  and there exist nonnegative functions
and there exist nonnegative functions  with
with  such that
such that

Then, BVP (1.1) has a unique unbounded positive solution.
Proof.
We first show that  implies
implies  . By (4.4), we have
. By (4.4), we have

By Lemma 4.1,  is completely continuous. Let
is completely continuous. Let  . Then,
. Then,  . Set
. Set

For any  , by (4.5), we have
, by (4.5), we have

Therefore,  for all
for all  , that is,
, that is,  for any
for any  . Then, Lemma 2.6 yields
. Then, Lemma 2.6 yields  , which implies that
, which implies that  has a fixed point
has a fixed point  . Let
. Let  . Then,
. Then,  is an unbounded positive solution of BVP (1.1).
is an unbounded positive solution of BVP (1.1).
Next, we show the uniqueness of positive solution for BVP (1.1). We will show that  is a contraction. In fact, by (4.4), we have
is a contraction. In fact, by (4.4), we have

So,  is indeed a contraction. The Banach contraction mapping principle yields the uniqueness of positive solution to BVP (1.1).
is indeed a contraction. The Banach contraction mapping principle yields the uniqueness of positive solution to BVP (1.1).
5. Examples
Example 5.1.
Consider the following BVP:

We have

Let

Then,  , and it is easy to prove that
, and it is easy to prove that  is satisfied. By direct calculations, we can obtain that
is satisfied. By direct calculations, we can obtain that  . By Theorem 3.1, BVP (5.1) has an unbounded solution.
. By Theorem 3.1, BVP (5.1) has an unbounded solution.
Example 5.2.
Consider the following BVP:

In this case, we have

Let

Then,  . By Theorem 4.2, BVP (5.4) has a unique unbounded positive solution.
. By Theorem 4.2, BVP (5.4) has a unique unbounded positive solution.
References
Bicadze AV, Samarskiĭ AA: Some elementary generalizations of linear elliptic boundary value problems. Doklady Akademii Nauk SSSR 1969, 185: 739-740.
II'in VA, Moiseev EI: Nonlocal boundary value problem of the first kind for a Sturm-Liouville operator in its differential and finite difference aspects. Differential Equations 1987, 23: 803-810.
II'in VA, Moiseev EI: Nonlocal boundary value problem of the second kind for a Sturm-Liouville operator. Differential Equations 1987, 23: 979-987.
Gupta CP: Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equation. Journal of Mathematical Analysis and Applications 1992,168(2):540-551. 10.1016/0022-247X(92)90179-H
Feng W, Webb JRL:Solvability of
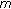 -point boundary value problems with nonlinear growth. Journal of Mathematical Analysis and Applications 1997,212(2):467-480. 10.1006/jmaa.1997.5520
-point boundary value problems with nonlinear growth. Journal of Mathematical Analysis and Applications 1997,212(2):467-480. 10.1006/jmaa.1997.5520Sun Y, Liu L: Solvability for a nonlinear second-order three-point boundary value problem. Journal of Mathematical Analysis and Applications 2004,296(1):265-275. 10.1016/j.jmaa.2004.04.013
Sun Y:Positive solutions of nonlinear second-order
 -point boundary value problem. Nonlinear Analysis. Theory, Methods & Applications 2005,61(7):1283-1294. 10.1016/j.na.2005.01.105
-point boundary value problem. Nonlinear Analysis. Theory, Methods & Applications 2005,61(7):1283-1294. 10.1016/j.na.2005.01.105Zhang X, Liu L, Wu C: Nontrivial solution of third-order nonlinear eigenvalue problems. Applied Mathematics and Computation 2006,176(2):714-721. 10.1016/j.amc.2005.10.017
Cheung W-S, Ren J:Positive solution for
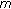 -point boundary value problems. Journal of Mathematical Analysis and Applications 2005,303(2):565-575. 10.1016/j.jmaa.2004.08.056
-point boundary value problems. Journal of Mathematical Analysis and Applications 2005,303(2):565-575. 10.1016/j.jmaa.2004.08.056Eloe PW, Ahmad B:Positive solutions of a nonlinear
 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009Atkinson FV, Peletier LA:Ground states of
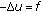 (
( ) and the Emden-Fowler equation. Archive for Rational Mechanics and Analysis 1986,93(2):103-127. 10.1007/BF00279955
) and the Emden-Fowler equation. Archive for Rational Mechanics and Analysis 1986,93(2):103-127. 10.1007/BF00279955Erbe L, Schmitt K: On radial solutions of some semilinear elliptic equations. Differential and Integral Equations 1988,1(1):71-78.
Kawano N, Yanagida E, Yotsutani S:Structure theorems for positive radial solutions to
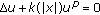 in
in  . Funkcialaj Ekvacioj 1993,36(3):557-579.
. Funkcialaj Ekvacioj 1993,36(3):557-579.Meehan M, O'Regan D: Existence theory for nonlinear Fredholm and Volterra integral equations on half-open intervals. Nonlinear Analysis. Theory, Methods & Applications 1999, 35: 355-387. 10.1016/S0362-546X(97)00719-0
Tian Y, Ge W: Positive solutions for multi-point boundary value problem on the half-line. Journal of Mathematical Analysis and Applications 2007,325(2):1339-1349. 10.1016/j.jmaa.2006.02.075
Lian H, Ge W: Solvability for second-order three-point boundary value problems on a half-line. Applied Mathematics Letters 2006,19(10):1000-1006. 10.1016/j.aml.2005.10.018
Yan B, O'Regan D, Agarwal RP: Unbounded solutions for singular boundary value problems on the semi-infinite interval: upper and lower solutions and multiplicity. Journal of Computational and Applied Mathematics 2006,197(2):365-386. 10.1016/j.cam.2005.11.010
Lian H, Ge W: Existence of positive solutions for Sturm-Liouville boundary value problems on the half-line. Journal of Mathematical Analysis and Applications 2006,321(2):781-792. 10.1016/j.jmaa.2005.09.001
Baxley JV: Existence and uniqueness for nonlinear boundary value problems on infinite intervals. Journal of Mathematical Analysis and Applications 1990,147(1):122-133. 10.1016/0022-247X(90)90388-V
Zima M: On positive solutions of boundary value problems on the half-line. Journal of Mathematical Analysis and Applications 2001,259(1):127-136. 10.1006/jmaa.2000.7399
Bai C, Fang J: On positive solutions of boundary value problems for second-order functional differential equations on infinite intervals. Journal of Mathematical Analysis and Applications 2003,282(2):711-731. 10.1016/S0022-247X(03)00246-4
Hao Z-C, Liang J, Xiao T-J: Positive solutions of operator equations on half-line. Journal of Mathematical Analysis and Applications 2006,314(2):423-435. 10.1016/j.jmaa.2005.04.004
Wang Y, Liu L, Wu Y: Positive solutions of singular boundary value problems on the half-line. Applied Mathematics and Computation 2008,197(2):789-796. 10.1016/j.amc.2007.08.013
Kang P, Wei Z: Multiple positive solutions of multi-point boundary value problems on the half-line. Applied Mathematics and Computation 2008,196(1):402-415. 10.1016/j.amc.2007.06.004
Zhang X: Successive iteration and positive solutions for a second-order multi-point boundary value problem on a half-line. Computers & Mathematics with Applications 2009,58(3):528-535. 10.1016/j.camwa.2009.04.015
Sun Y, Sun Y, Debnath L: On the existence of positive solutions for singular boundary value problems on the half-line. Applied Mathematics Letters 2009,22(5):806-812. 10.1016/j.aml.2008.07.009
Agarwal PR, O'Regan D: Infinite Interval Problems for Differential, Difference and Integral Equation. Kluwer Academic, Dodrecht, The Netherlands; 2001.
Guo DJ, Lakshmikantham V: Nonlinear problems in abstract cones. Volume 5. Academic Press, New York, NY, USA; 1988:viii+275.
Deimling K: Nonlinear Functional Analysis. Springer, Berlin, Germany; 1985:xiv+450.
Acknowledgments
The authors are grateful to the referees for valuable suggestions and comments. The first and second authors were supported financially by the National Natural Science Foundation of China (11071141, 10771117) and the Natural Science Foundation of Shandong Province of China (Y2007A23, Y2008A24). The third author was supported financially by the Australia Research Council through an ARC Discovery Project Grant.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, L., Hao, X. & Wu, Y. Unbounded Solutions of Second-Order Multipoint Boundary Value Problem on the Half-Line. Bound Value Probl 2010, 236560 (2010). https://doi.org/10.1155/2010/236560
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/236560
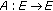 is well defined.
is well defined. is continuous.
is continuous.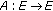 is relatively compact.
is relatively compact.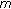 -point boundary value problems with nonlinear growth. Journal of Mathematical Analysis and Applications 1997,212(2):467-480. 10.1006/jmaa.1997.5520
-point boundary value problems with nonlinear growth. Journal of Mathematical Analysis and Applications 1997,212(2):467-480. 10.1006/jmaa.1997.5520 -point boundary value problem. Nonlinear Analysis. Theory, Methods & Applications 2005,61(7):1283-1294. 10.1016/j.na.2005.01.105
-point boundary value problem. Nonlinear Analysis. Theory, Methods & Applications 2005,61(7):1283-1294. 10.1016/j.na.2005.01.105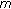 -point boundary value problems. Journal of Mathematical Analysis and Applications 2005,303(2):565-575. 10.1016/j.jmaa.2004.08.056
-point boundary value problems. Journal of Mathematical Analysis and Applications 2005,303(2):565-575. 10.1016/j.jmaa.2004.08.056 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009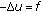 (
( ) and the Emden-Fowler equation. Archive for Rational Mechanics and Analysis 1986,93(2):103-127. 10.1007/BF00279955
) and the Emden-Fowler equation. Archive for Rational Mechanics and Analysis 1986,93(2):103-127. 10.1007/BF00279955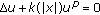 in
in  . Funkcialaj Ekvacioj 1993,36(3):557-579.
. Funkcialaj Ekvacioj 1993,36(3):557-579.