- Research Article
- Open access
- Published:
Multiple Positive Solutions for  th Order Multipoint Boundary Value Problem
th Order Multipoint Boundary Value Problem
Boundary Value Problems volume 2010, Article number: 708376 (2010)
Abstract
We study the existence of multiple positive solutions for  th-order multipoint boundary value problem.
th-order multipoint boundary value problem.  ,
,  ,
,  ,
,  , where
, where  ,
,  ,
,  . We obtained the existence of multiple positive solutions by applying the fixed point theorems of cone expansion and compression of norm type and Leggett-Williams fixed-point theorem. The results obtained in this paper are different from those in the literature.
. We obtained the existence of multiple positive solutions by applying the fixed point theorems of cone expansion and compression of norm type and Leggett-Williams fixed-point theorem. The results obtained in this paper are different from those in the literature.
1. Introduction
The existence of positive solutions for  th-order multipoint boundary problems has been studied by some authors (see [1, 2]). In [1], Pang et al. studied the expression and properties of Green's funtion and obtained the existence of at least one positive solution for
th-order multipoint boundary problems has been studied by some authors (see [1, 2]). In [1], Pang et al. studied the expression and properties of Green's funtion and obtained the existence of at least one positive solution for  th-order differential equations by applying means of fixed point index theory:
th-order differential equations by applying means of fixed point index theory:

where 
By using the fixed point theorems of cone expansion and compression of norm type, Yang and Wei in [2] also obtained the existence of at least one positive solutions for the BVP (1.1) if  . This work is motivated by Ma (see [3]). This method is simpler than that of [1]. In addition, Eloe and Ahmad in [4] had solved successfully the existence of positive solutions to the BVP (1.1) if
. This work is motivated by Ma (see [3]). This method is simpler than that of [1]. In addition, Eloe and Ahmad in [4] had solved successfully the existence of positive solutions to the BVP (1.1) if  = 1. Hao et al. in [5] had discussed the existence of at least two positive solutions for the BVP (1.1) by applying the Krasonse'skii-Guo fixed point theorem on cone expansion and compression if
= 1. Hao et al. in [5] had discussed the existence of at least two positive solutions for the BVP (1.1) by applying the Krasonse'skii-Guo fixed point theorem on cone expansion and compression if  = 1. However, there are few papers dealing with the existence of multiple positive solutions for
= 1. However, there are few papers dealing with the existence of multiple positive solutions for  th-order multipoint boundary value problem.
th-order multipoint boundary value problem.
In this paper, we study the existence of at least two positive solutions associated with the BVP (1.1) by applying the fixed point theorems of cone expansion and compression of norm type if  and the existence of at least three positive solutions for BVP (1.1) by using Leggett-Williams fixed-point theorem. The results obtained in this paper are different from those in the literature and essentially improve and generalize some well-known results (see [1–8]).
and the existence of at least three positive solutions for BVP (1.1) by using Leggett-Williams fixed-point theorem. The results obtained in this paper are different from those in the literature and essentially improve and generalize some well-known results (see [1–8]).
The rest of the paper is organized as follows. In Section 2, we present several lemmas. In Section 3, we give some preliminaries and the fixed point theorems of cone expansion and compression of norm type. The existence of at least two positive solutions for the BVP (1.1) is formulated and proved in Section 4. In Section 5, we give Leggett-Williams fixed-point theorem and obtain the existence of at least three positive solutions for the BVP (1.1).
2. Several Lemmas
Definition 2.1.
A function  is said to be a position of the BVP (1.1) if
is said to be a position of the BVP (1.1) if  satisfies the following:
satisfies the following:
() ;
;
() for
for  and satisfies boundary value conditions (1.1);
and satisfies boundary value conditions (1.1);
() hold for
hold for 
Lemma 2.2 (see [1]).
Suppose that

then for any  , the problem
, the problem

has a unique solution:

where

Lemma 2.3 (see [1]).
Let  ; Green's function
; Green's function  defined by (2.4) satisfies
defined by (2.4) satisfies

where  :
:

We omit the proof Lemma 2.3 here and you can see the detail of Theorem  in [1].
in [1].
Lemma 2.4 (see [2]).
Let  , and
, and  ; the unique solution
; the unique solution  of the BVP (2.2)
of the BVP (2.2)
satisfies

where  is defined by Lemma 2.3,
is defined by Lemma 2.3,  .
.
3. Preliminaries
In this section, we give some preliminaries for discussing the existence of multiple positive solutions of the BVP (1.1) in the next. In real Banach space  in which the norm is defined by
in which the norm is defined by

set

Obviously,  is a positive cone in
is a positive cone in  , where
, where  is from Lemma 2.3.
is from Lemma 2.3.
For convenience, we make the following assumptions:
() is continuous and
is continuous and  does not vanish identically, for
does not vanish identically, for  ;
;
() is continuous;
is continuous;
()
Let

where  is defined by (2.4).
is defined by (2.4).
From Lemmas 2.2–2.4, we have the following result.
Lemma 3.1 (see [2]).
Suppose that  are satisfied, then
are satisfied, then  is a completely continuous operator,
is a completely continuous operator,  , and the fixed points of the operator
, and the fixed points of the operator  in
in  are the positive solutions of the BVP (1.1).
are the positive solutions of the BVP (1.1).
For convenience, one introduces the following notations. Let

Problem 1.
Inspired by the work of the paper [2], whether we can obtain a similar conclusion or not, if

or

The aim of the following section is to establish some simple criteria for the existence of multiple positive solutions of the BVP (1.1), which gives a positive answer to the questions stated above. The key tool in our approach is the following fixed point theorem, which is a useful method to prove the existence of positive solutions for differential equations, for example [2–5, 9].
Suppose that  is a real Banach space and
is a real Banach space and  is cone in
is cone in  , and let
, and let  be two bounded open sets in
be two bounded open sets in  such that
such that  . Let operator
. Let operator  be completely continuous. Suppose that one of two conditions holds:
be completely continuous. Suppose that one of two conditions holds:
(i) for all
for all  for all
for all 
(ii) for all
for all  for all
for all  .
.
then  has at least one fixed point in
has at least one fixed point in 
4. The Existence of Two Positive Solutions
Theorem 4.1.
Suppose that the conditions  are satisfied and the following assumptions hold:
are satisfied and the following assumptions hold:
() ;
;
() ;
;
()There exists a constant  such that
such that  .
.
Then the BVP (1.1) has at least two positive solutions  and
and  such that
such that

Proof.
At first, it follows from the condition  that we may choose
that we may choose  such that
such that

Set  , and
, and  ; from (3.3) and (2.4) and Lemma 2.4, for
; from (3.3) and (2.4) and Lemma 2.4, for  , we have
, we have

Therefore, we have

Further, it follows from the condition  that there exists
that there exists  such that
such that

Let  , set
, set  , then
, then  and Lemma 2.4 imply
and Lemma 2.4 imply

and by the condition  , (2.4), (3.3), and Lemma 2.4, we have
, (2.4), (3.3), and Lemma 2.4, we have

Therefore, we have

Finally, let  and
and  . By (2.3), (3.3), and the condition
. By (2.3), (3.3), and the condition  , we have
, we have

which implies

Thus from (4.4)–(4.10) and Lemmas 3.1 and 3.2,  has a fixed point
has a fixed point  in
in  and a fixed
and a fixed  in
in  . Both are positive solutions of BVP (1.1) and satisfy
. Both are positive solutions of BVP (1.1) and satisfy

The proof is complete.
Corollary 4.2.
Suppose that the conditions  are satisfied and the following assumptions hold:
are satisfied and the following assumptions hold:
() ;
;
() ;
;
()there exists a constant  such that
such that 
Then the BVP (1.1) has at least two positive solutions  and
and  such that
such that

Proof.
From the conditions  , there exist sufficiently big positive constants
, there exist sufficiently big positive constants  such that
such that

by the condition  ; so all the conditions of Theorem 4.1 are satisfied; by an application of Theorem 4.1, the BVP (1.1) has two positive solutions
; so all the conditions of Theorem 4.1 are satisfied; by an application of Theorem 4.1, the BVP (1.1) has two positive solutions  and
and  such that
such that

Theorem 4.3.
Suppose that the conditions  are satisfied and the following assumptions hold:
are satisfied and the following assumptions hold:
() ;
;
() ;
;
()there exists a constant  such that
such that  .
.
Then the BVP (1.1) has at least two positive solutions  and
and  such that
such that

Proof.
It follows from the condition  that we may choose
that we may choose  such that
such that

Set  and
and  ; from (3.2) and (2.4), for
; from (3.2) and (2.4), for  , we have
, we have

Therefore, we have

It follows from the condition  that there exists
that there exists  such that
such that  for
for  and we consider two cases.
and we consider two cases.
Case i.
Suppose that  is unbounded; there exists
is unbounded; there exists  such that
such that  for
for  . Then for
. Then for  and
and  , we have
, we have

Case ii.
If  is bounded, that is,
is bounded, that is,  for all
for all  , taking
, taking  , for
, for  and
and  , we have
, we have

Hence, in either case, we always may set  such that
such that

Finally, set  ; then
; then  and Lemma 2.4 imply
and Lemma 2.4 imply

and by the condition  , (2.4), and (3.3), we have
, (2.4), and (3.3), we have

Hence, we have

From (4.18)–(4.24) and Lemmas 3.1 and 3.2,  has a fixed point
has a fixed point  in
in  and a fixed
and a fixed  in
in  . Both are positive solutions of the BVP(1.1) and satisfy
. Both are positive solutions of the BVP(1.1) and satisfy

The proof is complete.
Corollary 4.4.
Suppose that the conditions  are satisfied and the following assumptions hold:
are satisfied and the following assumptions hold:
() ;
;
() ;
;
()there exists a constant  such that
such that  .
.
Then BVP (1.1) has at least two positive solutions  and
and  such that
such that

The proof of Corollary 4.4 is similar to that of Corollary 4.2; so we omit it.
5. The Existence of Three Positive Solutions
Let  be a real Banach space with cone
be a real Banach space with cone  . A map
. A map  is said to be a nonnegative continuous concave functional on
is said to be a nonnegative continuous concave functional on  if
if  is continuous and
is continuous and

for all  and
and  Let
Let  be two numbers such that
be two numbers such that  and let
and let  be a nonnegative continuous concave functional on
be a nonnegative continuous concave functional on  . We define the following convex sets:
. We define the following convex sets:

Lemma 5.1 (see [12]).
Let  be completely continuous and let
be completely continuous and let  be a nonnegative continuous concave functional on
be a nonnegative continuous concave functional on  such that
such that  for
for  . Suppose that there exist
. Suppose that there exist  such that
such that
(i) and
and for
for
(ii) for
for
(iii) for
for  with
with 
Then  has at least three fixed points
has at least three fixed points  in
in  such that
such that

Now, we establish the existence conditions of three positive solutions for the BVP (1.1).
Theorem 5.2.
Suppose that  hold and there exist numbers
hold and there exist numbers  and
and  with
with  such that the following conditions are satisfied:
such that the following conditions are satisfied:



where

Then the boundary value problem (1.1) has at least three positive solutions.
Proof.
Let  be defined by (3.2) and let
be defined by (3.2) and let  be defined by (3.3). For
be defined by (3.3). For  , let
, let

Then it is easy to check that  is a nonnegative continuous concave functional on
is a nonnegative continuous concave functional on  with
with  for
for  and
and  is completely continuous.
is completely continuous.
First, we prove that if  holds, then there exists a number
holds, then there exists a number  and
and  To do this, by
To do this, by  , there exist
, there exist  and
and  such that
such that

Set

it follows that  for all
for all  . Take
. Take

If  , then
, then

that is,

Hence (5.10) show that if  holds, then there exists a number
holds, then there exists a number  such that
such that  maps
maps  into
into  .
.
Now we show that  and
and  for all
for all  . In fact, take
. In fact, take  , so
, so  . Moreover, for
. Moreover, for  , then
, then  , and we have
, and we have

Therfore, by  we obtain
we obtain

Next, we assert that  . In fact, if
. In fact, if  , by
, by  we have
we have

Hence,  for
for  .
.
Finally, we assert that if  and
and  , then
, then  . To see this, if
. To see this, if  and
and  ,then we have from Lemma 2.3 that
,then we have from Lemma 2.3 that

So we have

To sum up (5.10) (5.15), all the conditions of Lemma 5.1 are satisfied by taking
(5.15), all the conditions of Lemma 5.1 are satisfied by taking  . Hence, A has at least three fixed points; that is, BVP (1.1) has at least three positive solutions
. Hence, A has at least three fixed points; that is, BVP (1.1) has at least three positive solutions  , and
, and  such that
such that

The proof is complete.
References
Pang C, Dong W, Wei Z:Green's function and positive solutions of
 th order
th order 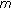 -point boundary value problem. Applied Mathematics and Computation 2006,182(2):1231-1239. 10.1016/j.amc.2006.05.010
-point boundary value problem. Applied Mathematics and Computation 2006,182(2):1231-1239. 10.1016/j.amc.2006.05.010Yang J, Wei Z:Positive solutions of
 th order
th order 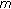 -point boundary value problem. Applied Mathematics and Computation 2008,202(2):715-720. 10.1016/j.amc.2008.03.009
-point boundary value problem. Applied Mathematics and Computation 2008,202(2):715-720. 10.1016/j.amc.2008.03.009Ma R: Positive solutions of a nonlinear three-point boundary-value problem. Electronic Journal of Differential Equations 1999,1999(34):1-8.
Eloe PW, Ahmad B:Positive solutions of a nonlinear
 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009Hao X, Liu L, Wu Y:Positive solutions for nonlinear
 th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.
th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.Ma R:Existence of positive solutions for second order
 -point boundary value problems. Annales Polonici Mathematici 2002,79(3):265-276. 10.4064/ap79-3-4
-point boundary value problems. Annales Polonici Mathematici 2002,79(3):265-276. 10.4064/ap79-3-4Ma R, Castaneda N:Existence of solutions of nonlinear
 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320Ma R: Multiplicity of positive solutions for second-order three-point boundary value problems. Computers & Mathematics with Applications 2000,40(2-3):193-204. 10.1016/S0898-1221(00)00153-X
Liu B: Positive solutions of fourth-order two point boundary value problems. Applied Mathematics and Computation 2004,148(2):407-420. 10.1016/S0096-3003(02)00857-3
Guo D: Nonlinear Functional Analysis. Shandong Science and Technology Press, Jinan, China; 2004.
Guo D, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Leggett RW, Williams LR: Multiple positive fixed points of nonlinear operators on ordered Banach spaces. Indiana University Mathematics Journal 1979,28(4):673-688. 10.1512/iumj.1979.28.28046
Acknowledgments
The authors are grateful to the referee's valuable comments and suggestions. The project is supported by the Natural Science Foundation of Anhui Province (KJ2010B226), The Excellent Youth Foundation of Anhui Province Office of Education (2009SQRZ169), and the Natural Science Foundation of Suzhou University (2009yzk17)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, Y., Wei, Z. Multiple Positive Solutions for  th Order Multipoint Boundary Value Problem.
Bound Value Probl 2010, 708376 (2010). https://doi.org/10.1155/2010/708376
th Order Multipoint Boundary Value Problem.
Bound Value Probl 2010, 708376 (2010). https://doi.org/10.1155/2010/708376
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/708376
 th order
th order 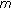 -point boundary value problem. Applied Mathematics and Computation 2006,182(2):1231-1239. 10.1016/j.amc.2006.05.010
-point boundary value problem. Applied Mathematics and Computation 2006,182(2):1231-1239. 10.1016/j.amc.2006.05.010 th order
th order 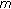 -point boundary value problem. Applied Mathematics and Computation 2008,202(2):715-720. 10.1016/j.amc.2008.03.009
-point boundary value problem. Applied Mathematics and Computation 2008,202(2):715-720. 10.1016/j.amc.2008.03.009 th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009
th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005,18(5):521-527. 10.1016/j.aml.2004.05.009 th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10.
th-order singular nonlocal boundary value problems. Boundary Value Problems 2007, 2007:-10. -point boundary value problems. Annales Polonici Mathematici 2002,79(3):265-276. 10.4064/ap79-3-4
-point boundary value problems. Annales Polonici Mathematici 2002,79(3):265-276. 10.4064/ap79-3-4 -point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320
-point boundary-value problems. Journal of Mathematical Analysis and Applications 2001,256(2):556-567. 10.1006/jmaa.2000.7320