- Research Article
- Open access
- Published:
Positive Solutions for Fourth-Order Singular  -Laplacian Differential Equations with Integral Boundary Conditions
-Laplacian Differential Equations with Integral Boundary Conditions
Boundary Value Problems volume 2010, Article number: 862079 (2010)
Abstract
By employing upper and lower solutions method together with maximal principle, we establish a necessary and sufficient condition for the existence of pseudo- as well as
as well as  positive solutions for fourth-order singular
positive solutions for fourth-order singular  -Laplacian differential equations with integral boundary conditions. Our nonlinearity
-Laplacian differential equations with integral boundary conditions. Our nonlinearity  may be singular at
may be singular at  ,
,  , and
, and  . The dual results for the other integral boundary condition are also given.
. The dual results for the other integral boundary condition are also given.
1. Introduction
In this paper, we consider the existence of positive solutions for the following nonlinear fourth-order singular  -Laplacian differential equations with integral boundary conditions:
-Laplacian differential equations with integral boundary conditions:

where  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  is nonnegative. Let
is nonnegative. Let  ,
,  . Throughout this paper, we always assume that
. Throughout this paper, we always assume that  ,
,  and nonlinear term
and nonlinear term  satisfies the following hypothesis:
satisfies the following hypothesis:
(H) is continuous, nondecreasing on
is continuous, nondecreasing on  and nonincreasing on
and nonincreasing on  for each fixed
for each fixed  , and there exists a real number
, and there exists a real number  such that, for any
such that, for any  ,
,

there exists a function  ,
,  and
and  is integrable on
is integrable on  such that
such that

Remark 1.1.
Condition  is used to discuss the existence and uniqueness of smooth positive solutions in [1].
is used to discuss the existence and uniqueness of smooth positive solutions in [1].
(i)Inequality (1.2) implies that

Conversely, (1.4) implies (1.2).
(ii)Inequality (1.3) implies that

Conversely, (1.5) implies (1.3).
Remark 1.2.
Typical functions that satisfy condition  are those taking the form
are those taking the form  =
=  , where
, where  ,
,  ,
,  ;
;  .
.
Remark 1.3.
It follows from (1.2) and (1.3) that

Boundary value problems with integral boundary conditions arise in variety of different areas of applied mathematics and physics. For example, heat conduction, chemical engineering, underground water flow, thermoelasticity, and plasma physics can be reduced to nonlocal problems with integral boundary conditions. They include two point, three point, and nonlocal boundary value problems (see [2–5]) as special cases and have attracted much attention of many researchers, such as Gallardo, Karakostas, Tsamatos, Lomtatidze, Malaguti, Yang, Zhang, and Feng (see [6–13], e.g.). For more information about the general theory of integral equations and their relation to boundary value problems, the reader is referred to the book by Corduneanu [14] and Agarwal and O'Regan [15].
Recently, Zhang et al. [13] studied the existence and nonexistence of symmetric positive solutions for the following nonlinear fourth-order boundary value problems:

where  ,
,  ,
,  ,
,  ,
,  is nonnegative, symmetric on the interval
is nonnegative, symmetric on the interval  ,
,  is continuous, and
is continuous, and  are nonnegative, symmetric on
are nonnegative, symmetric on  .
.
To seek necessary and sufficient conditions for the existence of solutions to the ordinary differential equations is important and interesting, but difficult. Professors Wei [16, 17], Du and Zhao [18], Graef and Kong [19], Zhang and Liu [20], and others have done much excellent work under some suitable conditions in this direction. To the author's knowledge, there are no necessary and sufficient conditions available in the literature for the existence of solutions for integral boundary value problem (1.1). Motivated by above papers, the purpose of this paper is to fill this gap. It is worth pointing out that the nonlinearity  permits singularity not only at
permits singularity not only at  but also at
but also at  . By singularity, we mean that the function
. By singularity, we mean that the function  is allowed to be unbounded at the points
is allowed to be unbounded at the points  and
and  .
.
2. Preliminaries and Several Lemmas
A function  and
and  is called a
is called a  (positive) solution of BVP (1.1) if it satisfies (1.1) (
(positive) solution of BVP (1.1) if it satisfies (1.1) ( for
for  ). A
). A  (positive) solution of (1.1) is called a psuedo-
(positive) solution of (1.1) is called a psuedo- (positive) solution if
(positive) solution if  ,
,  for
for  . Denote that
. Denote that

Definition 2.1.
A function  is called a lower solution of BVP (1.1) if
is called a lower solution of BVP (1.1) if  satisfies
satisfies

Definition 2.2.
A function  is called an upper solution of BVP (1.1) if
is called an upper solution of BVP (1.1) if  satisfies
satisfies

Suppose that  , and
, and

To prove the main results, we need the following maximum principle.
Lemma 2.3 (Maximum principle).
If  , such that
, such that  ,
,  , then
, then  ,
,  ,
, 
Proof.
Set





then  ,
,  ,
,  ,
,  and
and

Let

then


By integration of (2.12), we have

Integrating again, we get

Let  in (2.15), we obtain that
in (2.15), we obtain that

Substituting (2.13) and (2.16) into (2.15), we obtain that

where

Notice that

therefore,

Substituting (2.20) into (2.17), we have

where

Obviously,  ,
,  ,
,  . From (2.21), it is easily seen that
. From (2.21), it is easily seen that  for
for  By (2.11), we know that
By (2.11), we know that  that is,
that is,  Thus, we have proved that
Thus, we have proved that  ,
,  . Similarly, the solution of (2.5) and (2.7) can be expressed by
. Similarly, the solution of (2.5) and (2.7) can be expressed by

where

By (2.23), we can get that  ,
, 
Lemma 2.4.
Suppose that  holds. Let
holds. Let  be a
be a  positive solution of BVP (1.1). Then there exist two constants
positive solution of BVP (1.1). Then there exist two constants  such that
such that

Proof.
Assume that  is a
is a  positive solution of BVP (1.1). Then
positive solution of BVP (1.1). Then  can be stated as
can be stated as

where

It is easy to see that

By (2.26), for  , we have that
, we have that

From (2.26) and (2.27), we get that

Setting

then from (2.29) and (2.30), we have (2.25).
Lemma 2.5.
Suppose that  holds. And assume that there exist lower and upper solutions of BVP (1.1), respectively,
holds. And assume that there exist lower and upper solutions of BVP (1.1), respectively,  and
and  , such that
, such that  ,
,  for
for 
 . Then BVP (1.1) has at least one
. Then BVP (1.1) has at least one  positive solution
positive solution  such that
such that  ,
,  . If, in addition, there exists
. If, in addition, there exists  such that
such that

then the solution  of BVP (1.1) is a pseudo-
of BVP (1.1) is a pseudo- positive solution.
positive solution.
Proof.
For each  , for all
, for all  ,
,  , we defined an auxiliary function
, we defined an auxiliary function

By condition  , we have that
, we have that  is continuous.
is continuous.
Let  be sequences satisfying
be sequences satisfying  ,
,  and
and  as
as  and let
and let  ,
,  , be sequences satisfying
, be sequences satisfying

For each  , consider the following nonsingular problem:
, consider the following nonsingular problem:

For convenience, we define linear operators as follows:

By the proof of Lemma 2.3,  is a solution of problem (2.35) if and only if it is the fixed point of the following operator equation:
is a solution of problem (2.35) if and only if it is the fixed point of the following operator equation:

By (2.33), it is easy to verify that  is continuous and
is continuous and  is a bounded set. Moreover, by the continuity of
is a bounded set. Moreover, by the continuity of  , we can show that
, we can show that  is a compact operator and
is a compact operator and  is a relatively compact set. So,
is a relatively compact set. So,  is a completely continuous operator. In addition,
is a completely continuous operator. In addition,  is a solution of (2.35) if and only if
is a solution of (2.35) if and only if  is a fixed point of operator
is a fixed point of operator  . Using the Shauder's fixed point theorem, we assert that
. Using the Shauder's fixed point theorem, we assert that  has at least one fixed point
has at least one fixed point  , by
, by  , we can get
, we can get 
We claim that

From this it follows that

Indeed, suppose by contradiction that  on
on  . By the definition of
. By the definition of  , we have
, we have

Therefore,

On the other hand, since  is an upper solution of (1.1), we also have
is an upper solution of (1.1), we also have

Then setting

By (2.41) and (2.42), we obtain that

By Lemma 2.3, we can conclude that

Hence,

Set

Then

By Lemma 2.3, we can conclude that

which contradicts the assumption that  Therefore,
Therefore,  is impossible.
is impossible.
Similarly, we can show that  So, we have shown that (2.38) holds.
So, we have shown that (2.38) holds.
Using the method of [21] and Theorem  .2 in [22], we can obtain that there is a
.2 in [22], we can obtain that there is a  positive solution
positive solution  of (1.1) such that
of (1.1) such that  and a subsequence of
and a subsequence of  converging to
converging to  on any compact subintervals of
on any compact subintervals of  .
.
In addition, if (2.32) holds, then  . Hence,
. Hence,  is absolutely integrable on
is absolutely integrable on  . This implies that
. This implies that  is a pseudo-
is a pseudo- positive solution of (1.1).
positive solution of (1.1).
3. The Main Results
Theorem 3.1.
Suppose that  holds, then a necessary and sufficient condition for BVP (1.1) to have a pseudo-
holds, then a necessary and sufficient condition for BVP (1.1) to have a pseudo- positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

Proof.
The proof is divided into two parts, necessity and suffeciency.
Necessity.
Suppose that  is a pseudo-
is a pseudo- positive solution of (1.1). Then both
positive solution of (1.1). Then both  and
and  exist. By Lemma 2.4, there exist two constants
exist. By Lemma 2.4, there exist two constants  such that
such that

Without loss of generality, we may assume that  . This together with condition
. This together with condition  implies that
implies that

On the other hand, since  is a pseudo-
is a pseudo- positive solution of (1.1), we have
positive solution of (1.1), we have

Otherwise, let  . By the proof of Lemma 2.3, we have that
. By the proof of Lemma 2.3, we have that  ,
,  , that is,
, that is,  which contradicts that
which contradicts that  is a pseudo-
is a pseudo- positive solution. Therefore, there exists a positive
positive solution. Therefore, there exists a positive  such that
such that  . Obviously,
. Obviously,  . By (1.6) we have
. By (1.6) we have

Consequently,  , which implies that
, which implies that

It follows from (3.3) and (3.6) that

which is the desired inequality.
Sufficiency.
First, we prove the existence of a pair of upper and lower solutions. Since  is integrable on
is integrable on  , we have
, we have

Otherwise, if  , then there exists a real number
, then there exists a real number  such that
such that  when
when  , which contradicts the condition that
, which contradicts the condition that  is integrable on
is integrable on  . In view of condition
. In view of condition  and (3.8), we obtain that
and (3.8), we obtain that


where  .
.
Suppose that (3.1) holds. Firstly, we define the linear operators  and
and  as follows:
as follows:


where  is given by (2.27). Let
is given by (2.27). Let

It is easy to know from (3.11) and (3.12) that  By Lemma 2.4, we know that there exists a positive number
By Lemma 2.4, we know that there exists a positive number  such that
such that

Take  sufficiently small, then by (3.10), we get that
sufficiently small, then by (3.10), we get that  , that is,
, that is,

Let

Thus, from (3.14) and (3.16), we have

Considering  , it follows from (3.15), (3.17), and condition
, it follows from (3.15), (3.17), and condition  that
that

From (3.13) and (3.16), it follows that

Thus, we have shown that  and
and  are lower and upper solutions of BVP (1.1), respectively.
are lower and upper solutions of BVP (1.1), respectively.
Additionally, when  ,
,  , by (3.17) and condition
, by (3.17) and condition  , we have
, we have

From (3.1), we have  So, it follows from Lemma 2.5 that BVP (1.1) admits a pseudo-
So, it follows from Lemma 2.5 that BVP (1.1) admits a pseudo- positive solution such that
positive solution such that 
Remark 3.2.
Lin et al. [23, 24] considered the existence and uniqueness of solutions for some fourth-order and  conjugate boundary value problems when
conjugate boundary value problems when  , where
, where

under the following condition:
 for
for  and
and  , there exists
, there exists  such that
such that

Lei et al. [25] and Liu and Yu [26] investigated the existence and uniqueness of positive solutions to singular boundary value problems under the following condition:
 for all
for all  ,
,  where
where  and
and  is nondecreasing on
is nondecreasing on  and nonincreasing on
and nonincreasing on  .
.
Obviously, (3.21)-(3.22) imply condition  and condition
and condition  implies condition
implies condition  . So, condition
. So, condition  is weaker than conditions
is weaker than conditions  and
and  . Thus, functions considered in this paper are wider than those in [23–26].
. Thus, functions considered in this paper are wider than those in [23–26].
In the following, when  admits the form
admits the form  , that is, nonlinear term
, that is, nonlinear term  is not mixed monotone on
is not mixed monotone on  , but monotone with respect
, but monotone with respect  , BVP (1.1) becomes
, BVP (1.1) becomes

If  satisfies one of the following:
satisfies one of the following:
 is continuous, nondecreasing on
is continuous, nondecreasing on  , for each fixed
, for each fixed  , there exists a function
, there exists a function  ,
,  and
and  is integrable on
is integrable on  such that
such that

Theorem 3.3.
Suppose that  holds, then a necessary and sufficient condition for BVP (3.23) to have a pseudo-
holds, then a necessary and sufficient condition for BVP (3.23) to have a pseudo- positive solution is that the following integral condition holds
positive solution is that the following integral condition holds

Proof.
The proof is similar to that of Theorem 3.1; we omit the details.
Theorem 3.4.
Suppose that  holds, then a necessary and sufficient condition for problem (3.23) to have a
holds, then a necessary and sufficient condition for problem (3.23) to have a  positive solution is that the following integral condition holds
positive solution is that the following integral condition holds

Proof.
The proof is divided into two parts, necessity and suffeciency.
Necessity.
Assume that  is a
is a  positive solution of BVP (3.23). By Lemma 2.4, there exist two constants
positive solution of BVP (3.23). By Lemma 2.4, there exist two constants  and
and  ,
,  , such that
, such that

Let  be a constant such that
be a constant such that  . By condition
. By condition  , we have
, we have

By virtue of (3.28), we obtain that

By boundary value condition, we know that there exists a  such that
such that

For  by integration of (3.29), we get
by integration of (3.29), we get

Integrating (3.31), we have

Exchanging the order of integration, we obtain that

Similarly, by integration of (3.29), we get

Equations (3.33) and (3.34) imply that

Since  is a
is a  positive solution of BVP (1.1), there exists a positive
positive solution of BVP (1.1), there exists a positive  such that
such that  . Obviously,
. Obviously,  . On the other hand, choose
. On the other hand, choose  , then
, then  . By condition
. By condition  , we have
, we have

Consequently,  , which implies that
, which implies that

It follows from (3.35) and (3.37) that

which is the desired inequality.
Sufficiency.
Suppose that (3.26) holds. Let

It is easy to know, from (3.11) and (3.26), that

Thus, (3.12), (3.39), and (3.40) imply that  By Lemma 2.4, we know that there exists a positive number
By Lemma 2.4, we know that there exists a positive number  such that
such that

Take  sufficiently small, then by (3.10), we get that
sufficiently small, then by (3.10), we get that  , that is,
, that is,

Let

Thus, from (3.41) and (3.43), we have

Notice that  , it follows from (3.42)–(3.44) and condition
, it follows from (3.42)–(3.44) and condition  that
that

From (3.39) and (3.43), it follows that

Thus, we have shown that  and
and  are lower and upper solutions of BVP (1.1), respectively.
are lower and upper solutions of BVP (1.1), respectively.
From the first conclusion of Lemma 2.5, we conclude that problem (1.1) has at least one  positive solution
positive solution  .
.
4. Dual Results
Consider the fourth-order singular  -Laplacian differential equations with integral conditions:
-Laplacian differential equations with integral conditions:


Firstly, we define the linear operator  as follows:
as follows:

where  is given by (2.27).
is given by (2.27).
By analogous methods, we have the following results.
Assume that  is a
is a  positive solution of problem (4.1). Then
positive solution of problem (4.1). Then  can be expressed by
can be expressed by

Theorem 4.1.
Suppose that  holds, then a necessary and sufficient condition for (4.1) to have a pseudo-
holds, then a necessary and sufficient condition for (4.1) to have a pseudo- positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

Theorem 4.2.
Suppose that  holds, then a necessary and sufficient condition for problem (4.2) to have a pseudo-
holds, then a necessary and sufficient condition for problem (4.2) to have a pseudo- positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

Theorem 4.3.
Suppose that  holds, then a necessary and sufficient condition for problem (4.2) to have a
holds, then a necessary and sufficient condition for problem (4.2) to have a  positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

Consider the fourth-order singular  -Laplacian differential equations with integral conditions:
-Laplacian differential equations with integral conditions:


Define the linear operator  as follows:
as follows:

If  is a
is a  positive solution of problem (4.8). Then
positive solution of problem (4.8). Then  can be expressed by
can be expressed by

Theorem 4.4.
Suppose that  holds, then a necessary and sufficient condition for problem (4.8) to have a pseudo-
holds, then a necessary and sufficient condition for problem (4.8) to have a pseudo- positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

Theorem 4.5.
Suppose that  holds, then a necessary and sufficient condition for problem (4.9) to have a pseudo-
holds, then a necessary and sufficient condition for problem (4.9) to have a pseudo- positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

Theorem 4.6.
Suppose that  holds, then a necessary and sufficient condition for problem (4.9) to have a
holds, then a necessary and sufficient condition for problem (4.9) to have a  positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

Consider the fourth-order singular  -Laplacian differential equations with integral conditions:
-Laplacian differential equations with integral conditions:


Define the linear operator  as follows:
as follows:

If  is a
is a  positive solution of problem (4.15). Then
positive solution of problem (4.15). Then  can be expressed by
can be expressed by

Theorem 4.7.
Suppose that  holds, then a necessary and sufficient condition for problem (4.15) to have a pseudo-
holds, then a necessary and sufficient condition for problem (4.15) to have a pseudo- positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

Theorem 4.8.
Suppose that  holds, then a necessary and sufficient condition for problem (4.16) to have a pseudo-
holds, then a necessary and sufficient condition for problem (4.16) to have a pseudo- positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

Theorem 4.9.
Suppose that  holds, then a necessary and sufficient condition for problem (4.16) to have a
holds, then a necessary and sufficient condition for problem (4.16) to have a  positive solution is that the following integral condition holds:
positive solution is that the following integral condition holds:

References
Du X, Zhao Z:Existence and uniqueness of smooth positive solutions to a class of singular
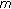 -point boundary value problems. Boundary Value Problems 2009, 2009:-13.
-point boundary value problems. Boundary Value Problems 2009, 2009:-13.Graef JR, Webb JRL: Third order boundary value problems with nonlocal boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 2009,71(5-6):1542-1551. 10.1016/j.na.2008.12.047
Graef JR, Yang B: Positive solutions of a third order nonlocal boundary value problem. Discrete and Continuous Dynamical Systems. Series S 2008,1(1):89-97.
Infante G, Webb JRL: Nonlinear non-local boundary-value problems and perturbed Hammerstein integral equations. Proceedings of the Edinburgh Mathematical Society. Series II 2006,49(3):637-656. 10.1017/S0013091505000532
Webb JRL, Infante G: Positive solutions of nonlocal boundary value problems: a unified approach. Journal of the London Mathematical Society. Second Series 2006,74(3):673-693. 10.1112/S0024610706023179
Gallardo JM: Second-order differential operators with integral boundary conditions and generation of analytic semigroups. The Rocky Mountain Journal of Mathematics 2000,30(4):1265-1292. 10.1216/rmjm/1021477351
Karakostas GL, Tsamatos PCh: Multiple positive solutions of some Fredholm integral equations arisen from nonlocal boundary-value problems. Electronic Journal of Differential Equations 2002, (30):1-17.
Lomtatidze A, Malaguti L: On a nonlocal boundary value problem for second order nonlinear singular differential equations. Georgian Mathematical Journal 2000,7(1):133-154.
Yang Z: Positive solutions to a system of second-order nonlocal boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2005,62(7):1251-1265. 10.1016/j.na.2005.04.030
Yang Z: Existence and nonexistence results for positive solutions of an integral boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2006,65(8):1489-1511. 10.1016/j.na.2005.10.025
Yang Z: Positive solutions of a second-order integral boundary value problem. Journal of Mathematical Analysis and Applications 2006,321(2):751-765. 10.1016/j.jmaa.2005.09.002
Feng M, Ji D, Ge W: Positive solutions for a class of boundary-value problem with integral boundary conditions in Banach spaces. Journal of Computational and Applied Mathematics 2008,222(2):351-363. 10.1016/j.cam.2007.11.003
Zhang X, Feng M, Ge W:Symmetric positive solutions for
 -Laplacian fourth-order differential equations with integral boundary conditions. Journal of Computational and Applied Mathematics 2008,222(2):561-573. 10.1016/j.cam.2007.12.002
-Laplacian fourth-order differential equations with integral boundary conditions. Journal of Computational and Applied Mathematics 2008,222(2):561-573. 10.1016/j.cam.2007.12.002Corduneanu C: Integral Equations and Applications. Cambridge University Press, Cambridge, UK; 1991:x+366.
Agarwal RP, O'Regan D: Infinite Interval Problems for Differential, Difference and Integral Equations. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001.
Wei Z:Positive solutions for
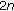 th-order singular sub-linear
th-order singular sub-linear 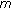 -point boundary value problems. Applied Mathematics and Computation 2006,182(2):1280-1295. 10.1016/j.amc.2006.05.014
-point boundary value problems. Applied Mathematics and Computation 2006,182(2):1280-1295. 10.1016/j.amc.2006.05.014Wei Z:A necessary and sufficient condition for
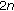 th-order singular super-linear
th-order singular super-linear 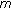 -point boundary value problems. Journal of Mathematical Analysis and Applications 2007,327(2):930-947. 10.1016/j.jmaa.2006.04.056
-point boundary value problems. Journal of Mathematical Analysis and Applications 2007,327(2):930-947. 10.1016/j.jmaa.2006.04.056Du X, Zhao Z: A necessary and sufficient condition of the existence of positive solutions to singular sublinear three-point boundary value problems. Applied Mathematics and Computation 2007,186(1):404-413. 10.1016/j.amc.2006.07.120
Graef JR, Kong L: Necessary and sufficient conditions for the existence of symmetric positive solutions of singular boundary value problems. Journal of Mathematical Analysis and Applications 2007,331(2):1467-1484. 10.1016/j.jmaa.2006.09.046
Zhang X, Liu L:A necessary and sufficient condition for positive solutions for fourth-order multi-point boundary value problems with
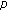 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008,68(10):3127-3137. 10.1016/j.na.2007.03.006
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008,68(10):3127-3137. 10.1016/j.na.2007.03.006Zhang Y: Positive solutions of singular sublinear Emden-Fowler boundary value problems. Journal of Mathematical Analysis and Applications 1994,185(1):215-222. 10.1006/jmaa.1994.1243
Hartman P: Ordinary Differential Equations. 2nd edition. Birkhäuser, Boston, Mass, USA; 1982:xv+612.
Lin X, Jiang D, Li X: Existence and uniqueness of solutions for singular fourth-order boundary value problems. Journal of Computational and Applied Mathematics 2006,196(1):155-161. 10.1016/j.cam.2005.08.016
Lin X, Jiang D, Li X:Existence and uniqueness of solutions for singular
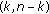 conjugate boundary value problems. Computers & Mathematics with Applications 2006,52(3-4):375-382. 10.1016/j.camwa.2006.03.019
conjugate boundary value problems. Computers & Mathematics with Applications 2006,52(3-4):375-382. 10.1016/j.camwa.2006.03.019Lei P, Lin X, Jiang D: Existence and uniqueness of positive solutions for singular nonlinear elliptic boundary value problems. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):2773-2779. 10.1016/j.na.2007.08.049
Liu Y, Yu H: Existence and uniqueness of positive solution for singular boundary value problem. Computers & Mathematics with Applications 2005,50(1-2):133-143. 10.1016/j.camwa.2005.01.022
Acknowledgments
The project is supported financially by a Project of Shandong Province Higher Educational Science and Technology Program (no. J10LA53) and the National Natural Science Foundation of China (no. 10971179).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, X., Cui, Y. Positive Solutions for Fourth-Order Singular  -Laplacian Differential Equations with Integral Boundary Conditions.
Bound Value Probl 2010, 862079 (2010). https://doi.org/10.1155/2010/862079
-Laplacian Differential Equations with Integral Boundary Conditions.
Bound Value Probl 2010, 862079 (2010). https://doi.org/10.1155/2010/862079
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/862079
 -point boundary value problems. Boundary Value Problems 2009, 2009:-13.
-point boundary value problems. Boundary Value Problems 2009, 2009:-13. -Laplacian fourth-order differential equations with integral boundary conditions. Journal of Computational and Applied Mathematics 2008,222(2):561-573. 10.1016/j.cam.2007.12.002
-Laplacian fourth-order differential equations with integral boundary conditions. Journal of Computational and Applied Mathematics 2008,222(2):561-573. 10.1016/j.cam.2007.12.002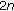 th-order singular sub-linear
th-order singular sub-linear 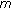 -point boundary value problems. Applied Mathematics and Computation 2006,182(2):1280-1295. 10.1016/j.amc.2006.05.014
-point boundary value problems. Applied Mathematics and Computation 2006,182(2):1280-1295. 10.1016/j.amc.2006.05.014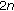 th-order singular super-linear
th-order singular super-linear 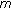 -point boundary value problems. Journal of Mathematical Analysis and Applications 2007,327(2):930-947. 10.1016/j.jmaa.2006.04.056
-point boundary value problems. Journal of Mathematical Analysis and Applications 2007,327(2):930-947. 10.1016/j.jmaa.2006.04.056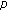 -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008,68(10):3127-3137. 10.1016/j.na.2007.03.006
-Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2008,68(10):3127-3137. 10.1016/j.na.2007.03.006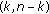 conjugate boundary value problems. Computers & Mathematics with Applications 2006,52(3-4):375-382. 10.1016/j.camwa.2006.03.019
conjugate boundary value problems. Computers & Mathematics with Applications 2006,52(3-4):375-382. 10.1016/j.camwa.2006.03.019