- Research Article
- Open access
- Published:
Existence and Multiplicity of Positive Solutions of a Boundary-Value Problem for Sixth-Order ODE with Three Parameters
Boundary Value Problems volume 2010, Article number: 878131 (2010)
Abstract
We study the existence and multiplicity of positive solutions of the following boundary-value problem:  ,
,  ,
,  , where
, where  R+ → R+ is continuous,
R+ → R+ is continuous,  ,
,  , and
, and  satisfy some suitable assumptions.
satisfy some suitable assumptions.
1. Introduction
The following boundary-value problem:

where  are some given real constants and
are some given real constants and  is a continuous function on
is a continuous function on  , is motivated by the study for stationary solutions of the sixth-order parabolic differential equations
, is motivated by the study for stationary solutions of the sixth-order parabolic differential equations

This equation arose in the formation of the spatial periodic patterns in bistable systems and is also a model for describing the behaviour of phase fronts in materials that are undergoing a transition between the liquid and solid state. When  it was studied by Gardner and Jones [1] as well as by Caginalp and Fife [2].
it was studied by Gardner and Jones [1] as well as by Caginalp and Fife [2].
If  is an even
is an even  periodic function with respect to
periodic function with respect to  and odd with respect to
and odd with respect to  , in order to get the
, in order to get the  stationary spatial periodic solutions of (1.2), one turns to study the two points boundary-value problem (1.1). The
stationary spatial periodic solutions of (1.2), one turns to study the two points boundary-value problem (1.1). The  periodic extension
periodic extension  of the odd extension of the solution
of the odd extension of the solution  of problems (1.1) to the interval
of problems (1.1) to the interval  yields
yields  spatial periodic solutions of(1.2)
spatial periodic solutions of(1.2)
Gyulov et al. [3] have studied the existence and multiplicity of nontrivial solutions of BVP (1.1). They gained the following results.
Theorem 1.1.
Let  be a continuous function and
be a continuous function and  . Suppose the following assumptions are held:
. Suppose the following assumptions are held:
 as
as  , uniformly with respect to
, uniformly with respect to  in bounded intervals,
in bounded intervals,
 as
as  , uniformly with respect to
, uniformly with respect to  in bounded intervals,
in bounded intervals,
then problem (1.1) has at least two nontrivial solutions provided that there exists a natural number  such that
such that  , where
, where  is the symbol of the linear differential operator
is the symbol of the linear differential operator  .
.
At the same time, in investigating such spatial patterns, some other high-order parabolic differential equations appear, such as the extended Fisher-Kolmogorov (EFK) equation

proposed by Coullet, Elphick, and Repaux in 1987 as well as by Dee and Van Saarlos in 1988 and Swift-Hohenberg (SH) equation

proposed in 1977.
In much the same way, the existence of spatial periodic solutions of both the EFK equation and the SH equation was studied by Peletier and Troy [4], Peletier and Rottschäfer [5], Tersian and Chaparova [6], and other authors. More precisely, in those papers, the authors studied the following fourth-order boundary-value problem:

The methods used in those papers are variational method and linking theorems.
On the other hand, The positive solutions of fourth-order boundary value problems (1.5) have been studied extensively by using the fixed point theorem of cone extension or compression. Here, we mention Li's paper [7], in which the author decomposes the fourth-order differential operator into the product of two second-order differential operators to obtain Green's function and then used the fixed point theorem of cone extension or compression to study the problem.
The purpose of this paper is using the idea of [7] to investigate BVP for sixth-order equations. We will discuss the existence and multiplicity of positive solutions of the boundary-value problem


and then we assume the following conditions throughout:
 is continuous,
is continuous,
 satisfy
satisfy

Note.
The set of  which satisfies
which satisfies  is nonempty. For instance, if
is nonempty. For instance, if  , then
, then  holds for
holds for  .
.
To be convenient, we introduce the following notations:

2. Preliminaries
Lemma 2.1 (see [8]).
Set the cubic equation with one variable as follows:

Let

one has the following:
-
(1)
Equation (2.1) has a triple root if
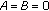 ,
, -
(2)
Equation (2.1) has a real root and two mutually conjugate imaginary roots if
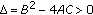 ,
, -
(3)
Equation (2.1) has three real roots, two of which are reroots if
 ,
, -
(4)
Equation (2.1) has three unequal real roots if
 .
.
Lemma 2.2.
Let  be the roots of the polynomial
be the roots of the polynomial  . Suppose that condition
. Suppose that condition  holds, then
holds, then  are real and greater than
are real and greater than  .
.
Proof.
There are  in the equation
in the equation  . Since condition
. Since condition  holds, we have
holds, we have

Therefore, the equation has three real roots in reply to Lemma 2.1.
By Vieta theorem, we have

Therefore  ,
,  and
and  hold if and only if
hold if and only if

Then, we only prove that the system of inequalities (2.5) holds if and only if  are all greater than
are all greater than  .
.
In fact, the sufficiency is obvious, we just prove the necessity. Assume that  are less than
are less than  . By the first inequality of (2.5), there exist two roots which are less than
. By the first inequality of (2.5), there exist two roots which are less than  and one which is greater than
and one which is greater than  . Without loss of generality, we assume that
. Without loss of generality, we assume that  , then we have
, then we have  . Multiplying the second inequality of (2.5) by
. Multiplying the second inequality of (2.5) by  , one gets
, one gets

Compare with the third inequality of (2.5), we have

which is a contradiction. Hence, the assumption is false. The proof is completed.
Let  be Green's function of the linear boundary-value problem
be Green's function of the linear boundary-value problem

Lemma 2.3 (see [7]).
 has the following properties:
has the following properties:
-
(i)
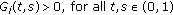 ,
, -
(ii)
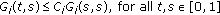 , where
, where 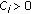 is a constant,
is a constant, -
(iii)
 , where
, where 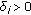 is a constant.
is a constant.
One denotes the following:

then  . Let
. Let  be the maximum norm of
be the maximum norm of  , and let
, and let  be the cone of all nonnegative functions in
be the cone of all nonnegative functions in  .
.
Let  , then one considers linear boundary-value problem (LBVP) as follows:
, then one considers linear boundary-value problem (LBVP) as follows:

with the boundary condition (1.7). Since

the solution of LBVP (2.10)–(1.7) can be expressed by

Lemma 2.4.
Let  , then the solution of LBVP(2.10)–(1.7) satisfies
, then the solution of LBVP(2.10)–(1.7) satisfies

Proof.
From (2.12) and (ii) of Lemma 2.3, it is easy to see that

and, therefore,

that is,

Using (iii) of Lemma 2.3, we have

The proof is completed.
We now define a mapping  by
by

It is clear that  is completely continuous. By Lemma 2.4, the positive solution of BVP(1.6)-(1.7) is equivalent to nontrivial fixed point of
is completely continuous. By Lemma 2.4, the positive solution of BVP(1.6)-(1.7) is equivalent to nontrivial fixed point of  . We will find the nonzero fixed point of
. We will find the nonzero fixed point of  by using the fixed point index theory in cones. For this, one chooses the subcone
by using the fixed point index theory in cones. For this, one chooses the subcone  of
of  by
by

where  , we have the following.
, we have the following.
Lemma 2.5.
Having  ,
,  is completely continuous.
is completely continuous.
Proof.
For  , let
, let  , then
, then  is the solution of LBVP(2.10)–(1.7). By Lemma 2.4, one has
is the solution of LBVP(2.10)–(1.7). By Lemma 2.4, one has

namely  . Therefore,
. Therefore,  . The complete continuity of
. The complete continuity of  is obvious.
is obvious.
The main results of this paper are based on the theory of fixed point index in cones [9]. Let  be a Banach space and
be a Banach space and  be a closed convex cone in
be a closed convex cone in  . Assume that
. Assume that  is a bounded open subset of
is a bounded open subset of  with boundary
with boundary  , and
, and  . Let
. Let  be a completely continuous mapping. If
be a completely continuous mapping. If  for every
for every  , then the fixed point index
, then the fixed point index  is well defined. We have that if
is well defined. We have that if  , then
, then  has a fixed point in
has a fixed point in  .
.
Let  and
and  for every
for every  .
.
Lemma 2.6 (see [9]).
Let  be a completely continuous mapping. If
be a completely continuous mapping. If  for every
for every  and
and  , then
, then  .
.
Lemma 2.7 (see [9]).
Let  be a completely continuous mapping. Suppose that the following two conditions are satisfied:
be a completely continuous mapping. Suppose that the following two conditions are satisfied:
-
(i)
 ,
, -
(ii)
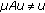 for every
for every 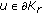 and
and  ,
,
then  .
.
Lemma 2.8 (see [9]).
Let  be a Banach space, and let
be a Banach space, and let  be a cone in
be a cone in  . For
. For  , define
, define  . Assume that
. Assume that  is a completely continuous mapping such that
is a completely continuous mapping such that  for every
for every  .
.
-
(i)
If
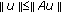 for every
for every  , then
, then  .
. -
(ii)
If
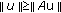 for every
for every 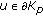 , then
, then 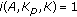 .
.
3. Existence
We are now going to state our existence results.
Theorem 3.1.
Assume that (H1) and (H2) hold, then in each of the following case:
-
(i)
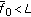 ,
, 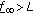 ,
, -
(ii)
 ,
, 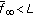 ,
,
the BVP(1.6)-(1.7) has at least one positive solution.
Proof.
To prove Theorem 3.1, we just show that the mapping  defined by (2.18) has a nonzero fixed point in the cases, respectively.
defined by (2.18) has a nonzero fixed point in the cases, respectively.
Case(i): since  , by the definition of
, by the definition of  , we may choose
, we may choose  and
and  so that
so that

Let  , we now prove that
, we now prove that  for every
for every  and
and  . In fact, if there exist
. In fact, if there exist  and
and  such that
such that  , then, by definition of
, then, by definition of  ,
,  satisfies differential equation the following:
satisfies differential equation the following:

and boundary condition (1.7). Multiplying (3.2) by  and integrating on
and integrating on  , then using integration by parts in the left side, we have
, then using integration by parts in the left side, we have

By Lemma 2.4,  , and then
, and then  . We see that
. We see that  , which is a contradiction. Hence,
, which is a contradiction. Hence,  satisfies the hypotheses of Lemma 2.6, in
satisfies the hypotheses of Lemma 2.6, in  . By Lemma 2.6 we have
. By Lemma 2.6 we have

On the other hand, since  , there exist
, there exist  and
and  such that
such that

Let  , then it is clear that
, then it is clear that

Choose  . Let
. Let  . Since
. Since  , from (3.5) we see that
, from (3.5) we see that

By Lemma 2.5, we have

Therefore,

from which we see that  , namely the hypotheses (i) of Lemma 2.7 holds. Next, we show that if
, namely the hypotheses (i) of Lemma 2.7 holds. Next, we show that if  is large enough, then
is large enough, then  for any
for any  and
and  . In fact, if there exist
. In fact, if there exist  and
and  such that
such that  , then
, then  satisfies (3.2) and boundary condition (1.7). Multiplying (3.2) by
satisfies (3.2) and boundary condition (1.7). Multiplying (3.2) by  and integrating, from (3.6) we have
and integrating, from (3.6) we have

Consequently, we obtain that

By Lemma 2.4,

from which and from (3.11) we get that

Let  , then for any
, then for any  and
and  ,
,  . Hence, hypothesis (ii) of Lemma 2.7 also holds. By Lemma 2.7, we have
. Hence, hypothesis (ii) of Lemma 2.7 also holds. By Lemma 2.7, we have

Now, by the additivity of fixed point index, combine (3.4) and (3.14) to conclude that

Therefore,  has a fixed point in
has a fixed point in  , which is the positive solution of BVP(1.6)-(1.7).
, which is the positive solution of BVP(1.6)-(1.7).
Case (ii): since  , there exist
, there exist  and
and  such that
such that

Let  , then for every
, then for every  , through the argument used in (3.9), we have
, through the argument used in (3.9), we have

Hence,  . Next, we show that
. Next, we show that  for any
for any  and
and  . In fact, if there exist
. In fact, if there exist  and
and  such that
such that  , then
, then  satisfies (3.2) and boundary (1.7). From (3.2) and (3.16), it follows that
satisfies (3.2) and boundary (1.7). From (3.2) and (3.16), it follows that

Since  , we see that
, we see that  , which is a contradiction. Hence, by Lemma 2.7, we have
, which is a contradiction. Hence, by Lemma 2.7, we have

On the other hand, since  , there exist
, there exist  and
and  such that
such that

Set  , we obviously have
, we obviously have

If there exist  and
and  such that
such that  , then (3.2) is valid. From (3.2) and (3.21), it follows that
, then (3.2) is valid. From (3.2) and (3.21), it follows that

By the proof of (3.13), we see that  . Let
. Let  , then for any
, then for any  and
and  ,
,  . Therefore, by Lemma 2.6, we have
. Therefore, by Lemma 2.6, we have

From (3.19) and (3.23), it follows that

Therefore,  has a fixed point in
has a fixed point in  , which is the positive solution of BVP(1.6)-(1.7). The proof is completed.
, which is the positive solution of BVP(1.6)-(1.7). The proof is completed.
From Theorem 3.1, we immediately obtain the following.
Corollary 3.2.
Assume that  and
and  hold, then in each of the following cases:
hold, then in each of the following cases:
-
(i)
 ,
,  ,
, -
(ii)
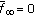 ,
,  ,
,
the BVP(1.6)-(1.7) has at least one positive solution.
4. Multiplicity
Next, we study the multiplicity of positive solutions of BVP(1.6)-(1.7) and assume in this section that
(H3) there is a  such that
such that  and
and  imply
imply  , where
, where  .
.
(H4) there is a  such that
such that  and
and  imply
imply  , where
, where  .
.
Theorem 4.1.
If  and
and  and
and  is satisfied, then BVP(1.6)-(1.7) has at least two positive solutions:
is satisfied, then BVP(1.6)-(1.7) has at least two positive solutions:  and
and  such that
such that  .
.
Proof.
According to the proof of Theorem 3.1, there exists  , such that
, such that  implies
implies  and
and  implies
implies  .
.
We now prove that  if
if  is satisfied. In fact, for every
is satisfied. In fact, for every  , from the definition of
, from the definition of  we have
we have

From (ii) of Lemma 2.8, we have

Combining (3.14) and (3.19), we have

Therefore,  has fixed points
has fixed points  and
and  in
in  and
and  , respectively, which means that
, respectively, which means that  and
and  are positive solutions of BVP(1.6)-(1.7) and
are positive solutions of BVP(1.6)-(1.7) and  . The proof is completed.
. The proof is completed.
Theorem 4.2.
If  and
and  and
and  is satisfied, then BVP(1.6)-(1.7) has at least two positive solutions:
is satisfied, then BVP(1.6)-(1.7) has at least two positive solutions:  and
and  such that
such that  .
.
Proof.
According to the proof of Theorem 3.1, there exists  , such that
, such that  implies
implies  and
and  implies
implies  .
.
We now prove that  if
if  is satisfied. In fact, for every
is satisfied. In fact, for every  , from the proof of (i) of Theorem 3.1, we have
, from the proof of (i) of Theorem 3.1, we have

Therefore,  , according to (i) of Lemma 2.8,
, according to (i) of Lemma 2.8,  .
.
Combining (3.4) and (3.23), we have

Therefore,  has the fixed points
has the fixed points  and
and  in
in  and
and  , respectively, which means that
, respectively, which means that  and
and  are positive solutions of BVP(1.6)-(1.7) and
are positive solutions of BVP(1.6)-(1.7) and  . The proof is completed.
. The proof is completed.
Theorem 4.3.
If  and
and  , and there exists
, and there exists  that satisfies
that satisfies
-
(i)
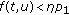 if
if 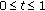 and
and  ,
, -
(ii)
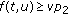 if
if 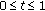 and
and 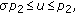
then BVP(1.6)-(1.7) has at least three positive solutions:  ,
,  and
and  such that
such that  .
.
Proof.
According to the proof of Theorem 3.1, there exists  , such that
, such that  implies
implies  and
and  implies
implies  .
.
From the proof of Theorems 4.1 and 4.2, we have

Combining the four afore-mentioned equations, we have

Therefore,  has the fixed points
has the fixed points  ,
,  and
and  in
in  ,
,  and
and  , which means that
, which means that  ,
,  and
and  are positive solutions of BVP(1.6)-(1.7) and
are positive solutions of BVP(1.6)-(1.7) and  . The proof is completed.
. The proof is completed.
References
Gardner RA, Jones CKRT: Traveling waves of a perturbed diffusion equation arising in a phase field model. Indiana University Mathematics Journal 1990,39(4):1197-1222. 10.1512/iumj.1990.39.39054
Caginalp G, Fife PC: Higher-order phase field models and detailed anisotropy. Physical Review. B 1986,34(7):4940-4943. 10.1103/PhysRevB.34.4940
Gyulov T, Morosanu G, Tersian S: Existence for a semilinear sixth-order ODE. Journal of Mathematical Analysis and Applications 2006,321(1):86-98. 10.1016/j.jmaa.2005.08.007
Peletier LA, Troy WC: Spatial Patterns, Progress in Nonlinear Differential Equations and their Applications. Volume 45. Birkhäuser Boston, Boston, Mass, USA; 2001:xvi+341.
Peletier LA, Rottschäfer V: Large time behaviour of solutions of the Swift-Hohenberg equation. Comptes Rendus Mathématique. Académie des Sciences. Paris 2003,336(3):225-230.
Tersian S, Chaparova J: Periodic and homoclinic solutions of extended Fisher-Kolmogorov equations. Journal of Mathematical Analysis and Applications 2001,260(2):490-506. 10.1006/jmaa.2001.7470
Li Y: Positive solutions of fourth-order boundary value problems with two parameters. Journal of Mathematical Analysis and Applications 2003,281(2):477-484. 10.1016/S0022-247X(03)00131-8
Fan S: The new root formula and criterion of cubic equation. Journal of Hainan Normal University 1989, 2: 91-98.
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, L., An, Y. Existence and Multiplicity of Positive Solutions of a Boundary-Value Problem for Sixth-Order ODE with Three Parameters. Bound Value Probl 2010, 878131 (2010). https://doi.org/10.1155/2010/878131
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/878131
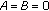 ,
,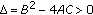 ,
, ,
, .
.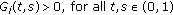 ,
,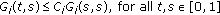 , where
, where 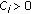 is a constant,
is a constant, , where
, where 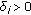 is a constant.
is a constant. ,
,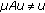 for every
for every 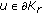 and
and  ,
,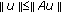 for every
for every  , then
, then  .
.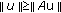 for every
for every 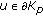 , then
, then 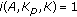 .
.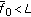 ,
, 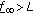 ,
, ,
, 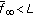 ,
, ,
,  ,
,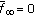 ,
,  ,
,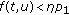 if
if 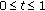 and
and  ,
,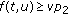 if
if 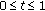 and
and