- Research
- Open access
- Published:
Singular limiting solutions for elliptic problem involving exponentially dominated nonlinearity and convection term
Boundary Value Problems volume 2011, Article number: 10 (2011)
Abstract
Given Ω bounded open regular set of ℝ2 and x1, x2, ..., x m ∈ Ω, we give a sufficient condition for the problem

to have a positive weak solution in Ω with u = 0 on ∂Ω, which is singular at each x i as the parameters ρ, λ > 0 tend to 0 and where f(u) is dominated exponential nonlinearities functions.
2000 Mathematics Subject Classification: 35J60; 53C21; 58J05.
1 Introduction and statement of the results
We consider the following problem

where ∇ is the gradient and Ω is an open smooth bounded subset of ℝ2. The function a is assumed to be positive and smooth. In the following, we take a(u) = eλu and f(u) = eλu(eu + eγu), for λ > 0 and γ ∈(0, 1), then problem (1) take the form

Using the following transformation

then the function w satisfies the following problem

with ϱ = (λρ2)1-λ. So when λ → 0+, the exponent  tends to infinity while the exponent
tends to infinity while the exponent  tends to -∞. For ϱ ≡ 0, problem (3) has been studied by Ren and Wei in [1]. See also [2].
tends to -∞. For ϱ ≡ 0, problem (3) has been studied by Ren and Wei in [1]. See also [2].
We denote by ε the smallest positive parameter satisfying

Remark that ρ ~ ε as ε → 0. We will suppose in the following

In particular, if we take  , then the condition (A
λ
) is satisfied. Under the assumption (A
λ
), we can treat equation (2) as a perturbation of the following:
, then the condition (A
λ
) is satisfied. Under the assumption (A
λ
), we can treat equation (2) as a perturbation of the following:

for γ ∈ (0, 1).
Our question is: Does there exist vε,λa sequence of solutions of (2) which converges to some singular function as the parameters ε and λ tend to 0?
In [3], Baraket et al. gave a positive answer to the above question for the following problem

with a regular bounded domain Ω of ℝ2. They give a sufficient condition for the problem (5) to have a weak solution in Ω which is singular at some points (x i )1≤i≤mas ρ and λ a small parameters satisfying (A λ ), where the presence of the gradient term seems to have significant influence on the existence of such solutions, as well as on their asymptotic behavior.
In case λ = 0 the authors in [4] gave also a positive answer for the following problem

for γ ∈ (0, 1) as ρ tends to 0. When λ = 0 and γ = 0, problem (2) reduce to

The study of this problem goes back to 1853 when Liouville derived a representation formula for all solutions of (7) which are defined in ℝ2, see [5]. It turns out that, beside the applications in geometry, elliptic equations with exponential nonlinearity also arise in modeling many physical phenomenon, such as thermionic emission, isothermal gas sphere, gas combustion, and gauge theory [6]. When ρ tends to 0, the asymptotic behavior of nontrivial branches of solutions of (7) is well understood thanks to the pioneer work of Suzuki [7] which characterizes the possible limit of nontrivial branches of solutions of (7). His result has been generalized in [8] to (6) with  , and finally by Ye in [9] to any exponentially dominated nonlinearity f(u). The existence of nontrivial branches of solutions with single singularity was first proved by Weston [10] and then a general result has been obtained by Baraket and Pacard [11]. These results were also extended, applying to the Chern-Simons vortex theory in mind, by Esposito et al. [12] and Del Pino et al. [13] to handle equations of the form -Δu = ρ2V(x)eu where V is a nonconstant positive potential. See also [14–16] wherever this rule is applicable. where the Laplacian is replaced by a more general divergence operator and some new phenomena occur. Let us also mention that the construction of nontrivial branches of solutions of semilinear equations with exponential nonlinearities allowed Wente to provide counter examples to a conjecture of Hopf [17] concerning the existence of compact (immersed) constant mean curvature surfaces in Euclidean space. Another related problem is the higher dimension problem with exponential nonlinearity. For example, the 4-dimensional semilinear elliptic problem with bi-Laplacian is treated in [18] and the problem with an additional singular source term given by Dirac masses is treated in [19] in the radial case. The results in [18, 19] are generalized to noncritical points of the reduced function, see [20].
, and finally by Ye in [9] to any exponentially dominated nonlinearity f(u). The existence of nontrivial branches of solutions with single singularity was first proved by Weston [10] and then a general result has been obtained by Baraket and Pacard [11]. These results were also extended, applying to the Chern-Simons vortex theory in mind, by Esposito et al. [12] and Del Pino et al. [13] to handle equations of the form -Δu = ρ2V(x)eu where V is a nonconstant positive potential. See also [14–16] wherever this rule is applicable. where the Laplacian is replaced by a more general divergence operator and some new phenomena occur. Let us also mention that the construction of nontrivial branches of solutions of semilinear equations with exponential nonlinearities allowed Wente to provide counter examples to a conjecture of Hopf [17] concerning the existence of compact (immersed) constant mean curvature surfaces in Euclidean space. Another related problem is the higher dimension problem with exponential nonlinearity. For example, the 4-dimensional semilinear elliptic problem with bi-Laplacian is treated in [18] and the problem with an additional singular source term given by Dirac masses is treated in [19] in the radial case. The results in [18, 19] are generalized to noncritical points of the reduced function, see [20].
We introduce now the Green's function G(x, x') defined on Ω × Ω, to be solution of

and let H(x, x') = G(x, x') + 4log |x - x'|, its regular part. Let m ∈ ℕ, we set

which is well defined in (Ω)m for x i ≠ x j for i ≠ j. Our main result is the following
Theorem 1 Given β ∈ (0, 1). Let Ω an open smooth bounded set of ℝ2, λ > 0 satisfying the condition (A λ ), γ ∈ (0, 1) and S = {x1, ... x m } ⊂ Ω be a nonempty set. Assume that, the point (x1, ..., x m ) is a nondegenerate critical point of the function

then there exist ε0 > 0, λ0 > 0 and  a family of solutions of (2), such that
a family of solutions of (2), such that

One of the purpose of the present paper is to present a rather efficient method: nonlinear Cauchy-data matching method to solve such singularly problems. This method has already been used successfully in geometric context (constant mean curvature surfaces, constant scalar curvature metrics, extremal Kähler metrics, manifolds with special holonomy, ...) and appeared in the study [18] in the context of partial differential equations.
2 Construction of the approximate solution
We first describe the rotationally symmetric approximate solutions of

in ℝ2 which will play a central role in our analysis. Given ε > 0, we define

which is clearly a solution of

in ℝ2. Let us notice that equations (11) is invariant under dilation in the following sense: If v is a solution of (11) and if τ > 0, then v(τ ·) + 2logτ is also a solution of (11). With this observation in mind, we define for all τ > 0

2.1 A linearized operator on ℝ2
For all ε, τ, λ > 0, we set

for δ ∈ (0, 1). We define the linear second order elliptic operator

which corresponds to the linearization of (11) about the solution u1 (= uε = τ = 1) given by (10) which has been defined in the previous section. We are interested in the classification of bounded solutions of  in ℝ2. Some solutions are easy to find. For example, we can define
in ℝ2. Some solutions are easy to find. For example, we can define

where r = |x|. Clearly  and this reflects the fact that (11) is invariant under the group of dilations τ → u(τ ·) + 2 logτ. We also define, for i = 1, 2
and this reflects the fact that (11) is invariant under the group of dilations τ → u(τ ·) + 2 logτ. We also define, for i = 1, 2

which are also solutions of  . Since, these solutions correspond to the invariance of the equation under the group of translations a → u(· + a). We recall the following result which classifies all bounded solutions of
. Since, these solutions correspond to the invariance of the equation under the group of translations a → u(· + a). We recall the following result which classifies all bounded solutions of  which are defined in ℝ2.
which are defined in ℝ2.
Lemma 1 [11] Any bounded solution of  defined in ℝ2 is a linear combination of ϕ
i
for i = 0, 1, 2.
defined in ℝ2 is a linear combination of ϕ
i
for i = 0, 1, 2.
Let B r denote the ball of radius r centered at the origin in ℝ2.
Definition 1 Given k ∈ ℕ, β ∈ (0, 1) and μ ∈ ℝ, we introduce the Hölder weighted spaces  as the space of functions
as the space of functions  for which the following norm
for which the following norm

is finite.
We define also

As a consequence of the result of Lemma 1, we recall the surjectivity result of  given in [11].
given in [11].
Proposition 1 [11]
-
(i)
Assume that μ > 1 and μ ∉ ℕ, then

is surjective.
-
(ii)
Assume that δ > 0 and δ ∉ ℕ then
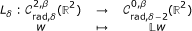
is surjective.
We set  , we define
, we define
Definition 2 Given k ∈ ℕ, β ∈ (0, 1) and μ ∈ ℝ, we introduce the Hölder weighted spaces  as the space of functions in
as the space of functions in  for which the following norm
for which the following norm

is finite.
Then, we define the subspace of radial functions in  by
by

We would like to find a solution u of

in  . By using the transformation,
. By using the transformation,  then Eq. (15) is equivalent to
then Eq. (15) is equivalent to

in  . We look for a solution of (16) of the form v(x) = u1(x) + h(x), this amounts to solve
. We look for a solution of (16) of the form v(x) = u1(x) + h(x), this amounts to solve

In  . We will need the following:
. We will need the following:
Definition 3 Given  , k∈ ∞, β ∈ (0, 1) and μ ∈ ℝ, the weighted space
, k∈ ∞, β ∈ (0, 1) and μ ∈ ℝ, the weighted space  is defined to be the space of functions
is defined to be the space of functions  endowed with the norm
endowed with the norm

For all σ ≥ 1, we denote by  the extension operator defined by
the extension operator defined by

where t α χ(t) is a smooth non-negative cutoff function identically equal to 1 for t ≤ 1 and identically equal to 0 for t ≥ 2. It is easy to check that there exists a constant c = c(μ) > 0, independent of σ ≥ 1, such that

We fix δ ∈ (0, 1) and denote by  to be a right inverse of
to be a right inverse of  provided by Proposition 1. To find a solution of (17), it is enough to find a fixed point h, in a small ball of
provided by Proposition 1. To find a solution of (17), it is enough to find a fixed point h, in a small ball of  , solution of
, solution of

We have

This implies that given κ > 0, there exist c κ > 0 (only depend on κ), such that for δ ∈ (0,1) and |x| = r, we have

Making use of Proposition 1 together with (19), we conclude that

Now, let h1, h2 such that  in
in  , then for δ ∈ (0, 1 - r] we have
, then for δ ∈ (0, 1 - r] we have

Similarly, making use of Proposition 1 together with condition (A
λ
) and (19), we conclude that given κ > 0, there exist ε
κ
> 0, λ
κ
> 0 and  (only depend on κ) such that
(only depend on κ) such that

Reducing λ
κ
> 0 and ε
κ
> 0 if necessary, we can assume that,  for all λ ∈ (0, λ
κ
) and ε ∈ (0, ε
κ
). Then, (21) and (22) are enough to show that h ↦ ℵ is a contraction from
for all λ ∈ (0, λ
κ
) and ε ∈ (0, ε
κ
). Then, (21) and (22) are enough to show that h ↦ ℵ is a contraction from  into itself and hence has a unique fixed point h in this set. This fixed point is solution of (20) in
into itself and hence has a unique fixed point h in this set. This fixed point is solution of (20) in  . We summarize this in the:
. We summarize this in the:
Proposition 2 Given δ ∈ (0, 1 - γ] and κ > 1, then there exist  (independent of ε and λ) and a unique
(independent of ε and λ) and a unique  with
with  such that
such that

solves (16) in  .
.
2.2 Analysis of the Laplace operator in weighted spaces
In this section, we study the mapping properties of the Laplace operator in weighted Hölder spaces. Given x1, ..., x m ∈ Ω, we define x := (x1, ..., x m )

and we choose r0 > 0 so that the balls  of center x
i
and radius r0 are mutually disjoint and included in Ω. For all r ∈ (0, r0), we define
of center x
i
and radius r0 are mutually disjoint and included in Ω. For all r ∈ (0, r0), we define

With these notations, we have:
Definition 4 Given k ∈ ℝ, β ∈ (0,1) and ν ∈ ℝ, we introduce the Hölder weighted space  as the space of functions
as the space of functions  for with the following norm
for with the following norm

is finite.
When k ≥ 2, we denote by  be the subspace of functions
be the subspace of functions  satisfying w = 0 on ∂Ω. We recall the
satisfying w = 0 on ∂Ω. We recall the
Proposition 3 [21] Assume that ν < 0 and ν ∉ ℤ, then

is surjective. Denote by  a right inverse of
a right inverse of  .
.
Remark 1 Observe that, when ν < 0, ν ∉ ℤ, the right inverse even though is not unique and can be chosen to depend smoothly on the points x1, ..., x m , at least locally. Once a right inverse is fixed for some choice of the points x1, ..., x m , a right inverse which depends smoothly on some points close to x1, ..., x m can be obtained using a simple perturbation argument. This argument will be used later in the nonlinear exterior problem, since we will move a little bit the points (x i ).
2.3 Harmonic extensions
We study the properties of interior and exterior harmonic extensions. Given  and define Hi (=Hi (φ; ·)) to be the solution of
and define Hi (=Hi (φ; ·)) to be the solution of

We denote by e1, e2 the coordinate functions on S1.
Lemma 2 [21] If we assume that

then there exists c > 0 such that

Given  , we define
, we define  to be the solution of
to be the solution of

which decays at infinity.
Definition 5 Given k ∈ ℕ, β ∈ (0,1) and ν ∈ ℝ, we define the space  as the space of functions
as the space of functions  for which the following norm
for which the following norm

is finite.
Lemma 3 [21] If we assume that

Then there exists c > 0 such that

If F ⊂ L2(S1) is a space of functions defined on S1, we define the space F⊥ to be the subspace of functions F of which are L2(S1) -orthogonal to the functions 1, e1,e2. We will need the:
Lemma 4 [21] The mapping

where Hi(= Hi (ψ; ·)) and He = He(ψ; ·), is an isomorphism.
3 The nonlinear interior problem
We are interested in studying equations of type

In  .
.
Given  satisfying (24), we define
satisfying (24), we define

Then, we look for a solution of (27) of the form w = v + v and using the fact that Hi is harmonic, this amounts to solve

We fix μ ∈ (1,2) and denote by  to be a right inverse of
to be a right inverse of  provided by Proposition 1. To find a solution of (28), it is sufficient to find
provided by Proposition 1. To find a solution of (28), it is sufficient to find  solution of
solution of

We denote by  , the nonlinear operator appearing on the right-hand side of equation (29).
, the nonlinear operator appearing on the right-hand side of equation (29).
Given κ > 0 (whose value will be fixed later on), we further assume that the functions φ satisfy

Then, we have the following result
Lemma 5 Given κ > 0. There exist ε
κ
> 0, λ
κ
> 0, c
κ
> 0 and  (only depend on κ) such that for all λ ∈ (0, λ
κ
) and ε ∈ (0, ε
κ
)
(only depend on κ) such that for all λ ∈ (0, λ
κ
) and ε ∈ (0, ε
κ
)

and

provided  satisfying
satisfying  .
.
Proof. The proof of the first estimate follows from the asymptotic behavior of Hi together with the assumption on the norm of boundary data φ given by (30). Indeed, let c κ be a constant depending only on κ (provided ε and λ are chosen small enough) it follows from the estimate of Hi, given by lemma 2, that

Since for each  , we have
, we have

where δ ∈ (0, 1 - γ]. Then

On the other hand, using the condition (A λ ), we have

and

Making use of Proposition 1 together with (20), we get

In order to derive the second estimate, we use the fact that, for  satisfying
satisfying  for i = 1,2, μ ∈ (1,2) and the condition (A
λ
), then there exist c
κ
> 0 (only depend on κ) such that
for i = 1,2, μ ∈ (1,2) and the condition (A
λ
), then there exist c
κ
> 0 (only depend on κ) such that

Similarly, making use of Proposition 1 together with (19), we conclude that there exists  (only depend on κ) such that
(only depend on κ) such that

□
Reducing λ
κ
> 0 and ε
κ
> 0 if necessary, we can assume that,  for all λ ∈ (0, λ
κ
) and ε ∈ (0, ε
κ
). Then, (31) and (32) are enough to show that
for all λ ∈ (0, λ
κ
) and ε ∈ (0, ε
κ
). Then, (31) and (32) are enough to show that  is a contraction from
is a contraction from  into itself and hence has a unique fixed point
into itself and hence has a unique fixed point  in this set. This fixed point is solution of (20) in ℝ2. We summarize this in the following:
in this set. This fixed point is solution of (20) in ℝ2. We summarize this in the following:
Proposition 4 Given κ > 0, there exist ε
κ
> 0, λ
κ
> 0 and c
κ
> 0 (only depending on κ) such that for all ε ∈ (0, ε
κ
), λ ∈ (0, λ
κ
) satisfying (A), for all τ in some fixed compact subset of [τ -, τ+] ⊂ (0, ∞) and for a given φ satisfying (24)-(30), then there exists a unique  solution of (29) such that
solution of (29) such that

Solve (27) in  . In addition,
. In addition,

Observe that the function  being obtained as a fixed point for contraction mappings, it depends continuously on the parameter τ.
being obtained as a fixed point for contraction mappings, it depends continuously on the parameter τ.
4 The nonlinear exterior problem
Recall that  denote the unique solution of
denote the unique solution of

in Ω, with  on ∂Ω. In addition, the following decomposition holds
on ∂Ω. In addition, the following decomposition holds

where  is a smooth function. Here, we give an estimate of the gradient of
is a smooth function. Here, we give an estimate of the gradient of  without proof (see [14], Lemma 2.1), there exists a constant c > 0, so that
without proof (see [14], Lemma 2.1), there exists a constant c > 0, so that

Let  close enough to x := (x1, ..., x
m
),
close enough to x := (x1, ..., x
m
),  close to 0 and
close to 0 and  satisfying (26). We define
satisfying (26). We define

where  is a cutoff function identically equal to 1 in
is a cutoff function identically equal to 1 in  and identically equal to 0 outside
and identically equal to 0 outside  .
.
We would like to find a solution of

in  which is a perturbation of
which is a perturbation of  . Writing
. Writing  . This amounts to solve
. This amounts to solve

We need to define some auxiliary weighted spaces:
Definition 6 Let  , k ∈ ℝ, β ∈ (0, 1) and ν ∈ ℝ, we define the Hölder weighted space
, k ∈ ℝ, β ∈ (0, 1) and ν ∈ ℝ, we define the Hölder weighted space  as the set of functions
as the set of functions  for which the following norm
for which the following norm

is finite
For all σ ∈ (0, r0/2) and all Y = (y1, ..., y m ) ∈ Ωm such that ||X - Y || ≤ r0/2, where X = (x1, ..., x m ), we denote by

the extension operator defined by  in
in 

for each i = 1, ..., m and  in each Bσ/2(y
i
), where
in each Bσ/2(y
i
), where  is a cutoff function identically equal to 1 for t ≥ 1 and identically equal to 0 for t ≤ 1/2. It is easy to check that there exists a constant c = c(ν) > 0 only depending on ν such that
is a cutoff function identically equal to 1 for t ≥ 1 and identically equal to 0 for t ≤ 1/2. It is easy to check that there exists a constant c = c(ν) > 0 only depending on ν such that

We fix

and denote by  a right inverse of Δ provided by Proposition 3 with
a right inverse of Δ provided by Proposition 3 with  . Clearly, it is enough to find
. Clearly, it is enough to find  solution of
solution of

where

We denote by  the nonlinear operator which appears on the right hand side of Eq.(36). Given κ > 0 (whose value will be fixed later on), we assume that the points
the nonlinear operator which appears on the right hand side of Eq.(36). Given κ > 0 (whose value will be fixed later on), we assume that the points  , the functions
, the functions  and the parameters
and the parameters  to satisfy
to satisfy


and

Then, the following result holds
Lemma 6 Given κ > 0, there exist ε
κ
> 0, λ
κ
> 0, c
κ
> 0 and  (depending on κ) such that for all ε ∈ (0, ε
κ
), λ ∈ (0, λ
κ
)
(depending on κ) such that for all ε ∈ (0, ε
κ
), λ ∈ (0, λ
κ
)

and

provided  and satisfy
and satisfy  .
.
Proof: Recall that  , we will estimate
, we will estimate  in different subregions of
in different subregions of  .
.
* In  , we have
, we have  ,
,  and
and

so that

Hence, for ν ∈ (- 1, 0) and for  small enough, we get
small enough, we get

* In  , we have
, we have  and
and  . Thus
. Thus

So, for ν ∈ (- 1, 0), we have

* In  , using the estimat (40), then we have
, using the estimat (40), then we have

where

Then

So,

Making use of Proposition 3 together with (34), we conclude that

For the proof of the second estimate, let  and
and  satisfying
satisfying  for i = 1,2, we have
for i = 1,2, we have

Then for γ ∈ (0,1), we get

So, for  small enough and using the estimate (35), there exist
small enough and using the estimate (35), there exist  (depending on κ ), such that:
(depending on κ ), such that:

□
Reducing λ
κ
> 0 and ε
κ
> 0 if necessary, we can assume that,  for all λ ∈ (0, λ
κ
) and ε ∈ (0, ε
κ
). Then, (42) and (43) are enough to show that
for all λ ∈ (0, λ
κ
) and ε ∈ (0, ε
κ
). Then, (42) and (43) are enough to show that  is a contraction from
is a contraction from  into itself and hence has a unique fixed point
into itself and hence has a unique fixed point  in this set. This fixed point is solution of (35). We summarize this in the following
in this set. This fixed point is solution of (35). We summarize this in the following
Proposition 5 Given κ > 0, there exists ε
κ
> 0 and λ
κ
> 0 (depending on κ) such that for all ε ∈ (0, ε
κ
) and λ ∈ (0, λ
κ
), for all set of parameter  satisfying (39) and function
satisfying (39) and function  satisfying (26), there exists a unique
satisfying (26), there exists a unique  solution of (36) such that
solution of (36) such that

As in the previous section, observe that the function  being obtained as a fixed point for contraction mapping, depends smoothly on the parameters
being obtained as a fixed point for contraction mapping, depends smoothly on the parameters  and the points
and the points  .
.
5 The nonlinear Cauchy-data matching
Keeping the notations of the previous sections, we gather the results of Proposition 4 and 5. Assume that  ∈ Ωm are given close to x := (x1, ..., x
m
) and satisfy (37). Assume also that τ := (τ1, ..., τ
m
) ∈ [τ
-
, τ +]m ⊂ (0, ∞)m are given (the values of τ- and τ + will be fixed shortly). First, we consider some set of boundary data
∈ Ωm are given close to x := (x1, ..., x
m
) and satisfy (37). Assume also that τ := (τ1, ..., τ
m
) ∈ [τ
-
, τ +]m ⊂ (0, ∞)m are given (the values of τ- and τ + will be fixed shortly). First, we consider some set of boundary data  satisfying (24). We set
satisfying (24). We set

According to the result of Proposition 4, we can find  a solution of
a solution of

in each  that can be decomposed as
that can be decomposed as

where the function  satisfies
satisfies

Similarly, given some boundary data  satisfying (26), some parameters
satisfying (26), some parameters  satisfying (38), provide ε ∈ (0, ε
κ
) and λ ∈ (0, λ
κ
), we use the result of Proposition 5, to find a solution v
ext
of (43) which can be decomposed as
satisfying (38), provide ε ∈ (0, ε
κ
) and λ ∈ (0, λ
κ
), we use the result of Proposition 5, to find a solution v
ext
of (43) which can be decomposed as

in  where, the function
where, the function  satisfies
satisfies

It remains to determine the parameters and the functions in such a way that the function which is equal to  in
in  and that is equal to vext in
and that is equal to vext in  is a smooth function. This amounts to find the boundary data and the parameters so that, for each i = 1 ..., m
is a smooth function. This amounts to find the boundary data and the parameters so that, for each i = 1 ..., m

on  . Assuming we have already done so, this provides for each ε and λ small enough a function
. Assuming we have already done so, this provides for each ε and λ small enough a function  (which is obtained by patching together the functions
(which is obtained by patching together the functions  and the function vext) solution of -Δv - λ |∇v|2 = ρ2 (ev + eγv) and elliptic regularity theory implies that this solution is in fact smooth. This will complete the proof of our result since, as ε and λ tend to 0, the sequence of solutions we have obtained satisfies the required properties, namely, away from the points x
i
the sequence vε,λconverges to
and the function vext) solution of -Δv - λ |∇v|2 = ρ2 (ev + eγv) and elliptic regularity theory implies that this solution is in fact smooth. This will complete the proof of our result since, as ε and λ tend to 0, the sequence of solutions we have obtained satisfies the required properties, namely, away from the points x
i
the sequence vε,λconverges to  . Before we proceed, the following remarks are due. First, it will be convenient to observe that the function
. Before we proceed, the following remarks are due. First, it will be convenient to observe that the function  can be expanded as
can be expanded as

near  . The function
. The function

which appear in the expression of v ext can be expanded as

Near  . Here, we have defined
. Here, we have defined

Thus for x near  , we have
, we have

where  .
.
Next, in (47), all functions are defined on  , but it will be convenient to solve the following equations
, but it will be convenient to solve the following equations

on S1. Here, all functions are considered as functions of y ∈ S1 and we have simply used the change of variables  to parameterize
to parameterize  .
.
Since the boundary data, we have chosen satisfy (24) and (26), we can decompose

where  are constant functions on S1,
are constant functions on S1,  belong to
belong to  and where
and where  are L2(S1) orthogonal to
are L2(S1) orthogonal to  and
and  . Projecting the equations (51) over
. Projecting the equations (51) over  will yield the system
will yield the system

Let us comment briefly on how these equations are obtained. They simply come from (51) when expansions (48) and (49) are used, together with the expression of Hi and He given in Lemma 2 and Lemma 3, and also the estimates (45) and (46). The system (52) can be readily simplified into

We are now in a position to define τ
-
and τ + since, according to the above, as ε and λ tend to 0 we expect that  will converge to x
i
and that τ
i
will converge to
will converge to x
i
and that τ
i
will converge to  satisfying
satisfying

and hence, it is enough to choose τ - and τ + in such a way that

We now consider the L2-projection of (51) over  . Given a smooth function f defined in Ω, we identify its gradient
. Given a smooth function f defined in Ω, we identify its gradient  with the element of
with the element of 

With these notations in mind, we obtain the equations

Finally, we consider the L2-projection onto L2(S1)⊥. This yields the system

Thanks to the result of Lemma 4, this last system can be re-written as

If we define the parameters t = (t i ) ∈ ℝm by

then, the system we have to solve reads

where as usual, the terms  depend nonlinearly on all the variables on the left side, but is bounded (in the appropriate norm) by a constant (independent of ε and λ) time
depend nonlinearly on all the variables on the left side, but is bounded (in the appropriate norm) by a constant (independent of ε and λ) time  , provide ε ∈ (0, ε
κ
) and λ ∈ (0, λ
κ
). Then, the nonlinear mapping which appears on the right-hand side of (55) is continuous and compact. In addition, reducing ε
κ
and λ
κ
if necessary, this nonlinear mapping sends the ball of radius
, provide ε ∈ (0, ε
κ
) and λ ∈ (0, λ
κ
). Then, the nonlinear mapping which appears on the right-hand side of (55) is continuous and compact. In addition, reducing ε
κ
and λ
κ
if necessary, this nonlinear mapping sends the ball of radius  (for the natural product norm) into itself, provided κ is fixed large enough. Applying Schauder's fixed Theorem in the ball of radius
(for the natural product norm) into itself, provided κ is fixed large enough. Applying Schauder's fixed Theorem in the ball of radius  in the product space where the entries live yields the existence of a solution of Eq. (55) and this completes the proof of our Theorem 1. □
in the product space where the entries live yields the existence of a solution of Eq. (55) and this completes the proof of our Theorem 1. □
References
Ren X, Wei J: On a two-dimensional elliptic problem with large exponent in nonlinearity. Trans Am Math Soc 1994, 343: 749-763.
Esposito P, Musso M, Pistoia A: Concentrating solutions for a planar problem involving nonlinearities with large exponent. J Diff Eqns 2006, 227: 29-68.
Baraket S, Ben Omrane I, Ouni T: Singular limits solutions for 2-dimensional elliptic problem involving exponential nonlinearities with non linear gradient term. Nonlinear Differ Equ Appl 2011, 18: 59-78.
Baraket S, Ye D: Singular limit solutions for two-dimensional elliptic problems with exponentionally dominated nonlinearity. Chin Ann Math Ser B 2001, 22: 287-296.
Liouville J:Sur l'équation aux différences partielles
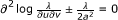 . J Math 1853, 18: 17-72.
. J Math 1853, 18: 17-72.Tarantello G: Multiple condensate solutions for the Chern-Simons-Higgs theory. J Math Phys 1996, 37: 3769-3796.
Suzuki T: Two dimensional Emden-Fowler Equation with Exponential Nonlinearity. Nonlinear Diffusion Equations and Their Equilibrium States Birkäuser 1992, 3: 493-512.
Nangasaki K, Suzuki T: Asymptotic analysis for two-dimensional elliptic eigenvalue problems with exponentially dominated nonlinearities. Asymptotic Anal 1990, 3: 173-188.
Ye D: Une remarque sur le comportement asymptotique des solutions de - Δ u = λ f ( u ). C R Acad Sci Paris I 1997, 325: 1279-1282.
Weston VH: On the asymptotique solution of a partial differential equation with exponential nonlinearity. SIAM J Math 1978, 9: 1030-1053.
Baraket S, Pacard F: Construction of singular limits for a semilinear elliptic equation in dimension 2. Calc Var Partial Differ Equ 1998, 6: 1-38.
Esposito P, Grossi M, Pistoia A: On the existence of Blowing-up solutions for a mean field equation. Ann I H Poincaré -AN 2005, 22: 227-257.
Del Pino M, Kowalczyk M, Musso M: Singular limits in Liouville-type equations. Calc Var Partial Differ Equ 2005, 24: 47-87.
Wei J, Ye D, Zhou F: Bubbling solutions for an anisotropic Emden-Fowler equation. Calc Var Partial Differ Equ 2007, 28: 217-247.
Wei J, Ye D, Zhou F: Analysis of boundary bubbling solutions for an anisotropic Emden-Fowler equation. Ann I H Poincaré AN 2008, 25: 425-447.
Ye D, Zhou F: A generalized two dimensional Emden-Fowler equation with exponential nonlinearity. Calc Var Partial Differ Equ 2001, 13: 141-158.
Wente HC: Counter example to a conjecture of H. Hopf. Pacific J Math 1986, 121: 193-243.
Baraket S, Dammak M, Ouni T, Pacard F: Singular limits for a 4-dimensional semilinear elliptic problem with exponential nonlinearity. Ann I H Poincaré AN 2007, 24: 875-895.
Dammak M, Ouni T: Singular limits for 4-dimensional semilinear elliptic problem with exponential nonlinearity adding a singular source term given by Dirac masses. Differ Int Equ 2008, 11-12: 1019-1036.
Clapp M, Munoz C, Musso M: Singular limits for the bi-Laplacian operator with exponential nonlinearity in ℝ4. Ann I H Poincaré AN 2008, 25: 1015-1041.
Baraket S, Ben Omrane I, Ouni T, Trabelsi N: Singular limits solutions for 2-dimensional elliptic problem with exponentially dominated nonlinearity and singular data. Communications in Contemporary Mathematics 2 2011, 13(4):129.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding the work through the research group project No RGP-VPP-087.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contribution
The authors declare that the work was realized in collaboration with same responsibility. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Baraket, S., Abid, I., Ouni, T. et al. Singular limiting solutions for elliptic problem involving exponentially dominated nonlinearity and convection term. Bound Value Probl 2011, 10 (2011). https://doi.org/10.1186/1687-2770-2011-10
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2011-10

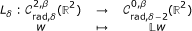
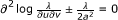 . J Math 1853, 18: 17-72.
. J Math 1853, 18: 17-72.