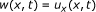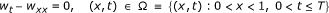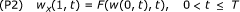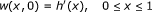- Research
- Open access
- Published:
An initial-boundary value problem for the one-dimensional non-classical heat equation in a slab
Boundary Value Problems volume 2011, Article number: 4 (2011)
Abstract
Nonlinear problems for the one-dimensional heat equation in a bounded and homogeneous medium with temperature data on the boundaries x = 0 and x = 1, and a uniform spatial heat source depending on the heat flux (or the temperature) on the boundary x = 0 are studied. Existence and uniqueness for the solution to non-classical heat conduction problems, under suitable assumptions on the data, are obtained. Comparisons results and asymptotic behavior for the solution for particular choices of the heat source, initial, and boundary data are also obtained. A generalization for non-classical moving boundary problems for the heat equation is also given.
2000 AMS Subject Classification: 35C15, 35K55, 45D05, 80A20, 35R35.
1. Introduction
In this article, we will consider initial and boundary value problems (IBVP), for the one-dimensional non-classical heat equation motivated by some phenomena regarding the design of thermal regulation devices that provides a heater or cooler effect [1–6]. In Section 2, we study the following IBVP (Problem (P1)):




where the unknown function u = u(x,t) denotes the temperature profile for an homogeneous medium occupying the spatial region 0 < x < 1, the boundary data f and g are real functions defined on ℝ+, the initial temperature h(x) is a real function defined on [0,1], and F is a given function of two real variables, which can be related to the evolution of the heat flux u x (0,t) (or of the temperature u(0,t)) on the fixed face x = 0. In Sections 6 and 7 the source term F is related to the evolution of the temperature u(0,t) when a heat flux u x (0,t) is given on the fixed face x = 0.
Non-classical problems like (1.1) to (1.4) are motivated by the modelling of a system of temperature regulation in isotropic media and the source term in (1.1) describes a cooling or heating effect depending on the properties of F which are related to the evolution of the heat u x (0,t). It is called the thermostat problem.
A heat conduction problem of the type (1.1) to (1.4) for a semi-infinite material was analyzed in [5, 6], where results on existence, uniqueness and asymptotic behavior for the solution were obtained. In other frameworks, a class of heat conduction problems characterized by a uniform heat source given as a multivalued function from ℝ into itself was studied in [3] with results regarding existence, uniqueness and asymptotic behavior for the solution. Other references on the subject are [2, 4, 7, 8]. Recently, free boundary problems (Stefan problems) for the non-classical heat equation have been studied in [9–11], where some explicit solutions are also given.
Section 2 is devoted to prove the existence and the uniqueness of the solution to an equivalent Volterra integral formulation for problems (1.1) to (1.4). In Section 3, 4 and 5, boundedness, comparisons results and asymptotic behavior regarding particular initial and boundary data are obtained. In Section 6, a similar problem to (P1) is presented: the heat source F depends on the temperature on the fixed face x = 0 when a heat flux boundary condition is imposed on x = 0, and we obtain the existence of a solution through a system of three second kind Volterra integral equations. In Section 7, we solve a more general problem for a non-classical heat equation with a moving boundary x = s(t) on the right side which generalizes the boundary constant case and it can be useful for the study of free boundary problems for the classical heat-diffusion equation [12].
2. Existence and uniquenes of problem (P1)
For data h = h(x), g = g(t), f = f(t) and F in problems (1.1) to (1.4) we shall consider the following assumptions:
(HA) g and f are continuously differentiable functions on ℝ+;
(HB) h is a continuously differentiable function in [0,1], which verifies the following compatibility conditions:

(HC) The function F = F(V,t) verifies the following conditions:
(HC1) The function F is defined and continuous in the domain ℝ × ℝ+;
(HC2) For each M > 0 and for |V| ≤ M, the function F is uniformly Hölder continuous in variable t for each compact subset of  ;
;
(HC3) For each bounded set B of ℝ × ℝ+, there exists a bounded positive function L 0 = L 0 (t), which is independent on B, defined for t > 0, such that

(HC4) The function F is bounded for bounded V for all t ≥ 0;
(HD) F(0,t) = 0, t > 0.
Under these assumptions, from Th. 20.3.3 of [13] an integral representation for the function u = u(x,t), which satisfies the conditions (1.1) to (1.4), can be written as below:

where θ = θ (x,t) is the known theta function defined by

and K = K(x,t) is the fundamental solution to the heat equation defined by:

Moreover the function V = V(t), defined by

as the heat flux on the face x = 0, must satisfy the following second kind Volterra integral equation

where

with  and K1 (x, t; ξ, τ) defined by
and K1 (x, t; ξ, τ) defined by


Taking into account that

and θ(-1,t) = θ(1,t), we can obtain a new expression for  given by
given by

Then, problem (2.2), (2.5) to (2.7) provides an integral formulation for the problem (1.1) to (1.4).
Theorem 1
Under the assumptions (HA) to (HC), there exists a unique solution to the problem (P1). Moreover, there exists a maximal time T > 0, such that the unique solution to (1.1) to (1.4) can be extended to the interval 0 ≤ t ≤ T.
Proof
In order to prove the existence and uniqueness of problem (P1) on the interval [0,T], we will verify the hypotheses (H1), (H2), (H3), (H5) and (H6) of the Theorem 1.2 of [[14], p. 91]. From (HA) and (HB) we conclude that V
o
(t) satisfies hypothesis (H1). From (HC1) and the continuity of  we conclude that
we conclude that  satisfies hypothesis (H2). If B is a bounded subset of D, then by (HC4) we have |F(V(τ),τ)| < M and, therefore, there exists m = m(t,τ) such that:
satisfies hypothesis (H2). If B is a bounded subset of D, then by (HC4) we have |F(V(τ),τ)| < M and, therefore, there exists m = m(t,τ) such that:

From (2.11), hypothesis (H3) holds. From the continuity of  and (HC4) we have hypothesis (H5). From (HC3), there exists
and (HC4) we have hypothesis (H5). From (HC3), there exists  such that for 0 ≤ τ ≤ t ≤ K, V1,V2 ∈ B:
such that for 0 ≤ τ ≤ t ≤ K, V1,V2 ∈ B:

then the hypothesis (H6) holds.
In order to extend the solution to a maximal interval we can apply the Theorem 2.3 [[14], p. 97]. Taking into account that function m = m(t,τ), defined in (2.11), verifies also the complementary condition:

then the required hypothesis (2.3) of [[14], p. 97] is fulfilled and the thesis holds.▀
3. Boundedness of the solution to problem (P1)
We obtain the following result.
Theorem 2
Under assumptions (HA) to (HD), the solution u to problem (P1) in [0,1] × [0,T], given by Theorem 1, is bounded in terms of the initial and boundary data h, f and g.
Proof
The integral representation of the solution u to problem (P1) can be written as

where

denotes the solution to (1.1) to (1.4) with null heat source (i.e. F ≡ 0 in such model).
From the continuity of function θ and hypothesis (HC3) and (HD), we have:

where M0 is a positive constant which verifies the inequality


and  , where we consider the bounded set [0,||V||] × [0,T]. Now, taking into account assumptions (HA), (HB) and properties of function θ, we can write
, where we consider the bounded set [0,||V||] × [0,T]. Now, taking into account assumptions (HA), (HB) and properties of function θ, we can write

where

and ζ represents the Riemann's Zeta function. From (2.6), (2.7) and hypothesis (HC3) and (HD), we have:

where

Finally, in view of (3.9) and inequality (2.10), we can apply the Gronwall inequality which provides:

and then, from (3.4) we obtain for 0 < t ≤ T the following estimation:

and the thesis holds.▀
4. Qualitative analysis of problem (P1)
In this section, we shall consider problem (1.1) to (1.4) with the following assumptions:

Lemma 3
-
(a)
Under the hypothesis (HD) and (HF), we have that w(0,t) > 0, ∀ t > 0, where w(x,t) is defined by
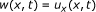 (4.1)
(4.1)
and u(x,t) is the solution to problem (P1);
-
(b)
Under the assumptions (HD), (HE) and (HF) we have that w(1,t) > 0, ∀ t > 0;
-
(c)
Under the assumptions of part (b) we have that w(x,t) > 0, ∀ x ∈ (0,1), ∀ t > 0;
-
(d)
Under the assumptions of part (b) we have that u(x,t) > 0, ∀ x ∈ [0,1], ∀ t > 0;
-
(e)
Under the assumptions of part (b) we have that u(x,t) ≤ u 1, ∀ x ∈ [0,1], ∀ t ≥ 0.
Proof
-
(a)
Let us first observe that w(x,t), defined in (4.1), is a solution to the following auxiliary problem (P2):
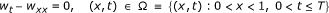 (4.2)
(4.2) (4.3)
(4.3)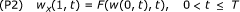 (4.4)
(4.4)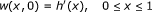 (4.5)
(4.5)
As w(x, 0) = h'(x) > 0 we have that the minimum of w(0,t) cannot be at x = 0. Suppose that there exists t o > 0 such that w(0,t o ) = 0. By the Maximum Principle we know that w x (0,t 0 ) > 0. Moreover, by assumption (HD), we have that w x (0,t o ) = F(w(0,t o ),t 0 ) = F(0,t o ) = 0, which is a contradiction. Therefore we have w(0,t) > 0, ∀ t > 0.
-
(b)
As w(1,0) > 0, we have that the minimum of w(1,t) cannot be at x = 0. Suppose that there exists t 1 > 0 such that w(1,t 1) = 0. By the maximum principle we have that w x (0,t 1) < 0. In other respects, we have that w x (1,t 1) = F(w(0,t 1),t 1) and by assumption (HE) follows that w(0,t 1) < 0, which is a contradiction. Therefore, we have w(1,t) > 0, ∀ t > 0.
-
(c)
It is sufficient to use part (a), (b), h'(x) > 0 and the maximum principle.
-
(d)
Let us observe that
 (4.6)
(4.6)
By assumption (HF) and part (c) we have that u(x,t) > 0, ∀ x ∈ [0,1], ∀ t ≥ 0.
-
(e)
Let us observe that u t - u xx < 0, which follows from (HE) and part (c). According to the Maximum Principle, the maximum of u(x,t) must be on the parabolic boundary, from which we obtain that
 (4.7)
(4.7)
and the result holds.▀
Lemma 4
Under the assumptions (HD), (HE) and (HF), we have that

Proof
Let v(x,t) = u(x,t) - u 0 (x,t), then v(x,t) is a solution to the following problem (P3):




From the maximum principle it follows that v(x,t) ≤ 0, ∀ x ∈ [0,1], ∀ t > 0.▀
Lemma 5
Under the same assumptions of Lemma 4, we have  .
.
Proof
Let us observe that u o (x,t) is a solution to the following problem (P4):




Therefore,  , and by Lemma 4, and (d) and (c) of Lemma 3, the thesis holds.▀
, and by Lemma 4, and (d) and (c) of Lemma 3, the thesis holds.▀
5. Local comparison results
Now we will consider the continuous dependence of the functions V = V(t) and u = u(x,t) given by (2.2) and (2.6), respectively, upon the data f, g, h and F. Let us denote by V i = V i (t) (i = 1,2) the solution to (2.6) in the minimum interval [0,T] and u i = u i (x,t) given by (2.2), respectively, for the data f i , g i , h i and F (i = 1,2) in problem (P1). Then we obtain the following results.
Theorem 6
Let us consider the problem (P1) under the assumptions (HA) to (HD), then we have:

and

Proof
From (2.6) and (2.7) we can write

Now, taking into account (HA), (HB), (HC3) and properties of function θ, we get:

where C2 and C3 are given by (3.10). Then, (5.1) follows from (5.4) by using the Gronwall's inequality. To obtain (5.2) we note that from (2.2) we can write

Now, taking into account assumptions (HA), (HB) and (HC), and using the same constants as in (3.5) and (3.7) it follows (5.2).▀
Now, let u i = u i (x,t), V i = V i (t) (i = 1,2) be the functions given by (2.2) and (2.6) for the data f, g, h and F i (i = 1,2) in problem (P1). Then, we obtain the following result:
Theorem 7
Let us consider the problem (P1) under the assumptions (HA) to (HD), then we obtain the following estimation:

where

Proof
From (2.6) and (2.7) we can write

Taking into account the inequality

from (5.7) and (2.10) we obtain

where  is given by (HC3), with respect to F2. Using a Gronwall's inequality it follows that
is given by (HC3), with respect to F2. Using a Gronwall's inequality it follows that

Besides, in view of (5.6), (5.8) and assumption (HC3), from (2.2) we get:

and the thesis holds.▀
6. Another related problem
Now, we will consider a new non-classical initial-boundary value problem (P5) for the heat equation in the slab [0,1], which is related to the previous problem (P1), i.e. (6.1) to (6.4):




The proof of their corresponding results follows a similar method to the one developed in previous Sections.
Theorem 8
Under the assumptions (HA) to (HD), the solution u to the problem (P5) has the expression

where V = V(t), defined by

must satisfy the following second kind Volterra integral equation

Proof
We follow the Theorem 1.▀
Theorem 9
Under the assumptions (HA) to (HD), there exists a unique solution to the problem (P5). Moreover, there exists a maximal time T > 0, such that the unique solution to (1.1) to (1.4) can be extended to the interval 0 ≤ t ≤ T.
Proof
It is similar to the one given for Theorem 1.▀
Theorem 10
Under the assumptions (HA) to (HD), the solution u to problem (P5) in [0,1]×[0,T] given by Theorem 9, it is bounded in terms of the initial and boundary data h, f and g, in the following way:

here C2 and C3 are given by (3.9) and

Let us denote by V i = V i (t) (i = 1,2) the solution to (6.7) and u i = u i (x,t) given by (6.5), respectively, for the data f i , g i , h i and F (i = 1,2) in problem (P5).
Theorem 11
Let us consider the problem (P5) under the assumptions (HA) to (HD), then we obtain the following estimations:


Proof
It is similar to the one given for Theorem 6.▀
Now, let u i = u i (x,t), V i = V i (t) (i = 1,2) be the functions given by (6.5) and (6.7) for the data f, g, h and F i (i = 1,2) in problem (P5), respectively.
Theorem 12
Let us consider the problem (P5) under the assumptions (HA) to (HD), then we obtain the following estimation:

Proof
It is similar to the one given for Theorem 7.▀
We consider the following assumptions:

Theorem 13
Under the hypotheses (HG) and (HE), we have that

Proof
Suppose that there exists t o > 0 such that u(0,t o ) = 0. By assumption (HE) we have that u t - u xx ≤ 0 for all 0 < x < 1, 0 < t ≤ t o . By applying the maximum principle we get u x (0,t o ) > 0 which is a contradiction. Then, it implies that u(0,t) > 0 for all t > 0. Therefore, by assumption (HE), we have that u t - u xx ≤ 0 for all (x,t) in Ω, and by the Maximum Principle, the minimum of u must be at t = 0, which implies, by assumption (HG), that u(x,t) > 0, ∀x ∈ [0,1], ∀t ≥ 0.
7. Non-classical moving boundary problems
In this Section, we will study some initial and boundary value problems for the non-classical heat equation in the domain

where s = s(t) is a continuous function of t over the interval t > 0 and s(0) = 1. The IBVP are reduced to equivalent systems of integral equations in order to get the existence of a solution.
We consider the following problem (P6):




The function F is now related to the evolution of the temperature instead of the heat flux at x = 0. The problem (P6) can be considered a non-classical moving boundary problem for the heat equation as a generalization of the moving boundary problem for the classical heat equation [13] which can be useful in the study of free boundary problems for the heat-diffusion equation [12].
We will use the Neumann function, which is defined by

Theorem 14
Under the assumptions (HA) to (HD) the solution u to the problem (P6) has the expression

where the function V, defined by

and the piecewise continuous functions ϕ1 and ϕ2 must satisfy the following system of three integral equations:



Conversely, if V, ϕ1 and ϕ 2 are solutions to the integral system (7.9)-(7.11), and u has the expression (7.7), then u is a solution to the problem (P6). Moreover, V(t) = u(0,t) and the solution u is unique among the class of solutions for which u x is bounded.
Proof
We first make a smooth extension of h outside of 0≤x≤1, so that the extended h is bounded and has compact support. The solution u is now assumed to have the form (7.7), where V, ϕ1 and ϕ 2 are unknown continuous functions that they are to be determined. Note that the initial condition (7.5) is satisfied. From the differential equation we obtain

and therefore by (7.8) the differential equation is satisfied. The system of integral equations is derived from the boundary conditions. The second equation is obtained allowing x to tend to s(t) and using the Lemma 14.2.3 of [13, page 218], i.e.,

Letting x to tend to zero in (7.7), we obtain the third equation, i.e.,

Now let us derive u with respect to x from (7.6) and we get,

When x tends to zero in (7.15), and using the jump formulae of the fundamental solution to the heat equation [15], we obtain

and the first integral equation holds. Consequently, if u possesses the form (6.7), then the functions V, ϕ1 and ϕ 2 must satisfy the system (7.9) to (7.11).
Moreover, if the continuous functions V, ϕ1 and ϕ 2 verify the system (7.9) to (7.11) for all 0 ≤ t ≤ T, then we can consider the expression (7.7) for u, which satisfies the initial condition (7.5). Allowing x to tend to zero in (7.15), and using (7.10) we obtain (7.8), and therefore the differential equation is satisfied. From Lemma 4.2.3 of [13, page 50] we see that

Hence, from (7.8) we have u x (0,t) = f(t). Likewise, u assumes the value g as x tends to s(t), and therefore the equivalence between (7.3) to (7.6) and (7.9) to (7.11) holds.
Finally, in order to prove the uniqueness and existence of solution to the system of integral equations (7.9) to (7.11), we will verify hypothesis (8.2.40) to (8.2.44) of the Corollary 8.2.1 of [13, p. 91]. First we define the following functions:



Now we will prove (8.2.40) [13]. We have for i = 1,2,3:

For the first function we have,

and by using the classical inequality

we deduce that

where  . For the second function, by using (HC3), we have
. For the second function, by using (HC3), we have

By using inequality (7.23), we can get

For the third function, by using (HC3), we have

and by using inequality (7.23), we get

If we define

the hypothesis (8.2.40) [13] is satisfied. Now let us prove (8.2.41) to (8.2.42) [13]. We have

where C4 and C5 are positive constants. Therefore we define the function α as follows:

which is an increasing function and tends to zero, when η tends to zero. Let us note that H i (t,τ,0,0,0) = 0 for all i = 1, 2,3, and therefore hypothesis (8.2.43) and (8.2.44) [13] are satisfied.▀
Now, we can consider the following problem (P7):




In this case, the function F depends on the evolution of the temperature of the temperature u(0,t) on the fixed face x = 0 while a heat flux condition is given by (7.33). This non-classical problem (P7) can be consider as a complementary problem to the previous problem (P1) given by (1.1) to (1.4) in which the source term F depends on the heat flux on the fixed face x = 0 while a temperature boundary condition (1.2) is given on the face x = 0.
Corollary 15
Under the same assumptions of Theorem 9, the solution u to the problem (P7) is given by the expression

and then the unknown function V, defined by (7.8), and the unknown piecewise continuous functions ϕ1 and ϕ 2 are the solution to the following system of three integral equations:



Conversely, if V, ϕ1 and ϕ 2 are solutions to the integral system (7.37) to (7.39), and we define u by the expression (7.36), then u is a solution to the problem (P7). Moreover, we have V(t) = u(0,t).
Theorem 16
Under the assumptions (HA) to (HD) the solution u to the problem (P8):




is given by:

where the unknown function V, defined by (7.8), and the unknown piecewise continuous functions ϕ1 and ϕ 2 are solutions to the following system of three integral equations:



Conversely, if V, ϕ1 and ϕ 2 are solutions to the integral system (7.45) to (7.47), and u has the form (7.44), then u is a solution to the problem (P8). Moreover, we have V(t) = u(0,t).
Proof
It is similar to the one given for Theorem 14.▀
Conclusions
In this article, we have proposed and obtained the existence and uniqueness of several initial-boundary value problems for the one-dimensional non-classical heat equation in the slab [0,1] with a heat source depending on the heat flux (or the temperature) on the boundary x = 0. Moreover, a generalization for non-classical moving boundary problems for the heat equation is also given.
References
Berrone LR, Tarzia DA, Villa LT: Asymptotic behavior of a Non-classical heat conduction problem for a semi-infinite material. Math Methods Appl Sci 2000, 23: 1161-1177. 10.1002/1099-1476(20000910)23:13<1161::AID-MMA157>3.0.CO;2-Y
Glashoff K, Sprekels K: The regulation of temperature by thermostats and set-valued integral equations. J Integral Equ 1982, 4: 95-112.
Kenmochi N, Primicerio M: One-dimensional heat conduction with a class of automatic heat source controls. IMA J Appl Math 1998, 40: 205-216.
Kenmochi N: Heat conduction with a class of automatic heat source controls. Pitman Research Notes in Mathematics Series, # 1990, 186: 471-474.
Tarzia DA, Villa LT: Some nonlinear heat conduction problems for a semi-infinite strip with a non-uniform heat source. Rev Un Mat Argentina 1998, 41: 99-114.
Villa LT: Problemas de control para una ecuación unidimensional del calor. Rev Un Mat Argentina 1986, 32: 163-169.
Cannon JR, Yin HM: A class of non-linear non-classical parabolic equations. J Diff Equ 1989, 79: 266-288. 10.1016/0022-0396(89)90103-4
Souplet P: Blow-up in nonlocal reaction-diffusion equations. SIAM J Math Anal 1998, 29: 1301-1334. 10.1137/S0036141097318900
Briozzo AC, Tarzia DA: Existence and uniqueness of a one-phase Stefan problem for a non-classical heat equation with temperature boundary condition at the fixed face. Electron J Diff Eq 2006, 2006(21):1-16.
Briozzo AC, Tarzia DA: A one-phase Stefan problem for a non-classical heat equation with a heat flux condition on the fixed face. Appl Math Comput 2006, 182: 809-819. 10.1016/j.amc.2006.04.043
Briozzo AC, Tarzia DA: Exact solutions for nonclassical Stefan problems. Int J Diff Eq 1-19. 2010, Article ID 868059
Tarzia DA: A bibliography on moving-free boundary problems for the heat-diffusion equation. The Stefan and related problems, MAT Ser A 2000, 2: 1-297. (with 5869 titles on the subject). Available from: [http://web.austral.edu.ar/descargas/facultad-cienciasEmpresariales/mat/Tarzia-MAT-SerieA-2(2000).pdf]
Cannon JR: The one-dimensional heat equation. Addison-Wesley Publishing Company, Menlo Park, CA; 1984.
Miller RK: Non lineal Volterra Integral Equations. W.A. Benjamin, Inc., California; 1971.
Friedman A: Partial Differential Equations of Parabolic Type. Prentice-Hall, Englewood Cliffs; 1964.
Acknowledgements
This paper was partially sponsored by the project PIP No. 0460 of CONICET - UA (Rosario, Argentina), and Grant FA9550-10-1-0023. The authors would like to thank the anonymous referee for a careful review and constructive comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
The authors declare that the work was realized in collaboration with the same responsibility. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Salva, N.N., Tarzia, D.A. & Villa, L.T. An initial-boundary value problem for the one-dimensional non-classical heat equation in a slab. Bound Value Probl 2011, 4 (2011). https://doi.org/10.1186/1687-2770-2011-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2011-4