- Research Article
- Open access
- Published:
Positive Solutions of  th-Order Nonlinear Impulsive Differential Equation with Nonlocal Boundary Conditions
th-Order Nonlinear Impulsive Differential Equation with Nonlocal Boundary Conditions
Boundary Value Problems volume 2011, Article number: 456426 (2011)
Abstract
This paper is devoted to study the existence, nonexistence, and multiplicity of positive solutions for the  th-order nonlocal boundary value problem with impulse effects. The arguments are based upon fixed point theorems in a cone. An example is worked out to demonstrate the main results.
th-order nonlocal boundary value problem with impulse effects. The arguments are based upon fixed point theorems in a cone. An example is worked out to demonstrate the main results.
1. Introduction
The theory of impulsive differential equations describes processes which experience a sudden change of their state at certain moments. Processes with such a character arise naturally and often, especially in phenomena studied in physics, chemical technology, population dynamics, biotechnology, and economics. For an introduction of the basic theory of impulsive differential equations, see Lakshmikantham et al. [1]; for an overview of existing results and of recent research areas of impulsive differential equations, see Benchohra et al. [2]. The theory of impulsive differential equations has become an important area of investigation in the recent years and is much richer than the corresponding theory of differential equations; see, for instance, [3–14] and their references.
At the same time, a class of boundary value problems with integral boundary conditions arise naturally in thermal conduction problems [15], semiconductor problems [16], hydrodynamic problems [17]. Such problems include two, three, and multipoint boundary value problems as special cases and attract much attention; see, for instance, [7, 8, 11, 18–44] and references cited therein. In particular, we would like to mention some results of Eloe and Ahmad [19] and Pang et al. [22]. In [19], by applying the fixed point theorem in cones due to the work of Krasnosel'kii and Guo, Eloe and Ahmad established the existence of positive solutions of the following  th boundary value problem:
th boundary value problem:

In [22], Pang et al. considered the expression and properties of Green's function for the  th-order
th-order  -point boundary value problem
-point boundary value problem

where  . Furthermore, they obtained the existence of positive solutions by means of fixed point index theory.
. Furthermore, they obtained the existence of positive solutions by means of fixed point index theory.
Recently, Yang and Wei [23] and the author of [24] improved and generalized the results of Pang et al. [22] by using different methods, respectively.
On the other hand, it is well known that fixed point theorem of cone expansion and compression of norm type has been applied to various boundary value problems to show the existence of positive solutions; for example, see [7, 8, 11, 19, 23, 24]. However, there are few papers investigating the existence of positive solutions of  th impulsive differential equations by using the fixed point theorem of cone expansion and compression. The objective of the present paper is to fill this gap. Being directly inspired by [19, 22], using of the fixed point theorem of cone expansion and compression, this paper is devoted to study a class of nonlocal BVPs for
th impulsive differential equations by using the fixed point theorem of cone expansion and compression. The objective of the present paper is to fill this gap. Being directly inspired by [19, 22], using of the fixed point theorem of cone expansion and compression, this paper is devoted to study a class of nonlocal BVPs for  th-order impulsive differential equations with fixed moments.
th-order impulsive differential equations with fixed moments.
Consider the following  th-order impulsive differential equations with integral boundary conditions:
th-order impulsive differential equations with integral boundary conditions:

Here  (where
(where  is fixed positive integer) are fixed points with
is fixed positive integer) are fixed points with  where
where  and
and  represent the right-hand limit and left-hand limit of
represent the right-hand limit and left-hand limit of  at
at  , respectively,
, respectively,  is nonnegative.
is nonnegative.
For the case of  , problem (1.3) reduces to the problem studied by Samoĭlenko and Perestyuk in [4]. By using the fixed point index theory in cones, the authors obtained some sufficient conditions for the existence of at least one or two positive solutions to the two-point BVPs.
, problem (1.3) reduces to the problem studied by Samoĭlenko and Perestyuk in [4]. By using the fixed point index theory in cones, the authors obtained some sufficient conditions for the existence of at least one or two positive solutions to the two-point BVPs.
Motivated by the work above, in this paper we will extend the results of [4, 19, 22–24] to problem (1.3). On the other hand, it is also interesting and important to discuss the existence of positive solutions for problem (1.3) when  , and
, and  . Many difficulties occur when we deal with them; for example, the construction of cone and operator. So we need to introduce some new tools and methods to investigate the existence of positive solutions for problem (1.3). Our argument is based on fixed point theory in cones [45].
. Many difficulties occur when we deal with them; for example, the construction of cone and operator. So we need to introduce some new tools and methods to investigate the existence of positive solutions for problem (1.3). Our argument is based on fixed point theory in cones [45].
To obtain positive solutions of (1.3), the following fixed point theorem in cones is fundamental which can be found in [45, page 93].
Lemma 1.1.
Let  and
and  be two bounded open sets in Banach space
be two bounded open sets in Banach space  , such that
, such that  and
and  . Let
. Let  be a cone in
be a cone in  and let operator
and let operator  be completely continuous. Suppose that one of the following two conditions is satisfied:
be completely continuous. Suppose that one of the following two conditions is satisfied:
-
(i)
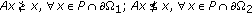 ;
; -
(ii)
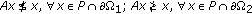 .
.
Then,  has at least one fixed point in
has at least one fixed point in  .
.
2. Preliminaries
In order to define the solution of problem (1.3), we will consider the following space.
Let  , and
, and

Then  is a real Banach space with norm
is a real Banach space with norm

where 
A function  is called a solution of problem (1.3) if it satisfies (1.3).
is called a solution of problem (1.3) if it satisfies (1.3).
To establish the existence of multiple positive solutions in  of problem (1.3), let us list the following assumptions:
of problem (1.3), let us list the following assumptions:
 ;
;
 , where
, where  .
.
Lemma 2.1.
Assume that  and
and  hold. Then
hold. Then  is a solution of problem (1.3) if and only if
is a solution of problem (1.3) if and only if  is a solution of the following impulsive integral equation:
is a solution of the following impulsive integral equation:

where



Proof.
First suppose that  is a solution of problem (1.3). It is easy to see by integration of (1.3) that
is a solution of problem (1.3). It is easy to see by integration of (1.3) that

Integrating again and by boundary conditions, we can get

Similarly, we get

Letting  in (2.9), we find
in (2.9), we find

Substituting  and (2.10) into (2.9), we obtain
and (2.10) into (2.9), we obtain

Multiplying (2.11) with  and integrating it, we have
and integrating it, we have

that is,

Then we have

Then, the proof of sufficient is complete.
Conversely, if  is a solution of (2.3), direct differentiation of (2.3) implies that, for
is a solution of (2.3), direct differentiation of (2.3) implies that, for  ,
,

Evidently,


So  and
and  , and it is easy to verify that
, and it is easy to verify that  , and the lemma is proved.
, and the lemma is proved.
Similar to the proof of that from [22], we can prove that  , and
, and  have the following properties.
have the following properties.
Proposition 2.2.
The function  defined by (2.5) satisfyong
defined by (2.5) satisfyong  is continuous for all
is continuous for all  .
.
Proposition 2.3.
There exists  such that
such that

where  is defined in (2.20).
is defined in (2.20).
Proposition 2.4.
If  , then one has
, then one has
(i) is continuous for all
is continuous for all  ;
;
(ii) .
.
Proof.
From the properties of  and the definition of
and the definition of  , we can prove that the results of Proposition 2.4 hold.
, we can prove that the results of Proposition 2.4 hold.
Proposition 2.5.
If  , the function
, the function  defined by (2.4) satisfies
defined by (2.4) satisfies
(i) is continuous for all
is continuous for all  ;
;
(ii) for each
for each  , and
, and

where  , and
, and

 is defined in Proposition 2.3.
is defined in Proposition 2.3.
Proof.
-
(i)
From Propositions 2.2 and 2.4, we obtain that
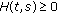 is continuous for all
is continuous for all 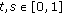 , and
, and 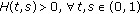 .
. -
(ii)
From (ii) of Proposition 2.2 and (ii) of Proposition 2.4, we have
 for each
for each  .
.
Now, we show that (2.19) holds.
In fact, from Proposition 2.3, we have

Then the proof of Proposition 2.5 is completed.
Remark 2.6.
From the definition of  , it is clear that
, it is clear that  .
.
Lemma 2.7.
Assume that  and
and  hold. Then, the solution
hold. Then, the solution  of problem (1.3) satisfies
of problem (1.3) satisfies 
Proof.
It is an immediate subsequence of the facts that  on
on  .
.
Remark 2.8.
From (ii) of Proposition 2.5, one can find that

For the sake of applying Lemma 1.1, we construct a cone  in
in  by
by

Define  by
by

Lemma 2.9.
Assume that  and
and  hold. Then,
hold. Then,  , and
, and  is completely continuous.
is completely continuous.
Proof.
From Proposition 2.5 and (2.24), we have

Thus,  .
.
Next, by similar arguments to those in [8] one can prove that  is completely continuous. So it is omitted, and the lemma is proved.
is completely continuous. So it is omitted, and the lemma is proved.
3. Main Results
Write

where  denotes
denotes  or
or 
In this section, we apply Lemma 1.1 to establish the existence of positive solutions for BVP (1.3).
Theorem 3.1.
Assume that  and
and  hold. In addition, letting
hold. In addition, letting  and
and  satisfy the following conditions:
satisfy the following conditions:
 and
and  ;
;
 or
or  ,
,
BVP (1.3) has at least one positive solution.
Proof.
Considering  , there exists
, there exists  such that
such that

where  satisfy
satisfy

here

Now, for  , we prove that
, we prove that

In fact, if there exists  such that
such that  . Noticing (3.2), then we have
. Noticing (3.2), then we have

where

Therefore,  , which is a contraction. Hence, (3.2) holds.
, which is a contraction. Hence, (3.2) holds.
Next, turning to  . Case (
. Case ( ).
).  . There exists
. There exists  such that
such that

where  . Choose
. Choose

We show that

In fact, if there exists  such that
such that  , then
, then

This and (3.9) imply that

So, we have

that is,

It is easy to see that

In fact, if  , then
, then  , for
, for  . Since
. Since  . Hence,
. Hence,  , which contracts
, which contracts  So, (3.15) holds. Therefore,
So, (3.15) holds. Therefore,  , this is also a contraction. Hence, (3.10) holds.
, this is also a contraction. Hence, (3.10) holds.
Case ( ).
).  . There exists
. There exists  such that
such that

where  . If we define
. If we define  , then
, then  . Choose
. Choose

We prove that (3.10) holds.
In fact, if there exists  such that
such that  , then
, then

This and (3.17) imply that

So, we have

From (3.20), we obtain that

So, we have

From the definition of  , we can find that
, we can find that

Similar to the proof in case ( ), we can show that
), we can show that  . Then, from (3.23), we have
. Then, from (3.23), we have  , which is a contraction. Hence, (3.10) holds.
, which is a contraction. Hence, (3.10) holds.
Applying (i) of Lemma 1.1 to (3.2) and (3.10) yields that  has a fixed point
has a fixed point  . Thus, it follows that BVP (1.3) has at least one positive solution, and the theorem is proved.
. Thus, it follows that BVP (1.3) has at least one positive solution, and the theorem is proved.
Theorem 3.2.
Assume that  and
and  hold. In addition, letting
hold. In addition, letting  and
and  satisfy the following conditions:
satisfy the following conditions:
 and
and  ;
;
 or
or  ,
,
BVP (1.3) has at least one positive solution.
Proof.
Considering  , there exists
, there exists  such that
such that  , for
, for  , where
, where  satisfy
satisfy  .
.
Similar to the proof of (3.2), we can show that

Next, turning to  . Under condition
. Under condition  , similar to the proof of (3.10), we can also show that
, similar to the proof of (3.10), we can also show that

Applying (i) of Lemma 1.1 to (3.24) and (3.25) yields that  has a fixed point
has a fixed point  . Thus, it follows that BVP (1.3) has one positive solution, and the theorem is proved.
. Thus, it follows that BVP (1.3) has one positive solution, and the theorem is proved.
Theorem 3.3.
Assume that  and
and  hold. In addition, letting
hold. In addition, letting  and
and  satisfy the following condition:
satisfy the following condition:
there is a  such that
such that  and
and  implies
implies

where  satisfy
satisfy  , BVP (1.3) has at least two positive solutions
, BVP (1.3) has at least two positive solutions  and
and  with
with  .
.
Proof.
We choose  with
with  . If
. If  holds, similar to the proof of (3.2), we can prove that
holds, similar to the proof of (3.2), we can prove that

If  holds, similar to the proof of (3.24), we have
holds, similar to the proof of (3.24), we have

Finally, we show that

In fact, if there exists  with
with  then by (2.23), we have
then by (2.23), we have

and it follows from  that
that

that is,  , which is a contraction. Hence, (3.29) holds.
, which is a contraction. Hence, (3.29) holds.
Applying Lemma 1.1 to (3.27), (3.28), and (3.29) yields that  has two fixed points
has two fixed points  with
with  . Thus it follows that BVP (1.3) has two positive solutions
. Thus it follows that BVP (1.3) has two positive solutions  with
with  . The proof is complete.
. The proof is complete.
Our last results corresponds to the case when problem (1.3) has no positive solution. Write

Theorem 3.4.
Assume  , and
, and  , then problem (1.3) has no positive solution.
, then problem (1.3) has no positive solution.
Proof.
Assume to the contrary that problem (1.3) has a positive solution, that is,  has a fixed point
has a fixed point  . Then
. Then  for
for  , and
, and

which is a contradiction, and this completes the proof.
To illustrate how our main results can be used in practice we present an example.
Example 3.5.
Consider the following boundary value problem:

Conclusion.
BVP (3.34) has at least one positive solution.
Proof.
BVP (3.34) can be regarded as a BVP of the form (1.3), where

It is not difficult to see that conditions  and
and  hold. In addition,
hold. In addition,

Then, conditions  and
and  of Theorem 3.1 hold. Hence, by Theorem 3.1, the conclusion follows, and the proof is complete.
of Theorem 3.1 hold. Hence, by Theorem 3.1, the conclusion follows, and the proof is complete.
References
Lakshmikantham V, Baĭnov DD, Simeonov PS: Theory of Impulsive Differential Equations, Series in Modern Applied Mathematics. World Scientific, Teaneck, NJ, USA; 1989:xii+273.
Benchohra M, Henderson J, Ntouyas S: Impulsive Differential Equations and Inclusions, Contemporary Mathematics and Its Applications. Volume 2. Hindawi, New York, NY, USA; 2006:xiv+366.
Baĭnov DD, Simeonov PS: Systems with Impulse Effect, Ellis Horwood Series: Mathematics and Its Applications. Ellis Horwood, Chichester, UK; 1989:255.
Samoĭlenko AM, Perestyuk NA: Impulsive Differential Equations, World Scientific Series on Nonlinear Science. Series A: Monographs and Treatises. Volume 14. World Scientific, River Edge, NJ, USA; 1995:x+462.
Lin X, Jiang D: Multiple positive solutions of Dirichlet boundary value problems for second order impulsive differential equations. Journal of Mathematical Analysis and Applications 2006, 321(2):501-514. 10.1016/j.jmaa.2005.07.076
Zhang X, Feng M, Ge W: Existence of solutions of boundary value problems with integral boundary conditions for second-order impulsive integro-differential equations in Banach spaces. Journal of Computational and Applied Mathematics 2010, 233(8):1915-1926. 10.1016/j.cam.2009.07.060
Zhang X, Yang X, Ge W: Positive solutions of n th-order impulsive boundary value problems with integral boundary conditions in Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2009, 71(12):5930-5945. 10.1016/j.na.2009.05.016
Agarwal RP, O'Regan D: Multiple nonnegative solutions for second order impulsive differential equations. Applied Mathematics and Computation 2000, 114(1):51-59. 10.1016/S0096-3003(99)00074-0
Liu B, Yu J: Existence of solution of m -point boundary value problems of second-order differential systems with impulses. Applied Mathematics and Computation 2002, 125(2-3):155-175. 10.1016/S0096-3003(00)00110-7
Feng M, Du Bo, Ge W: Impulsive boundary value problems with integral boundary conditions and one-dimensional p -Laplacian. Nonlinear Analysis. Theory, Methods & Applications 2009, 70(9):3119-3126. 10.1016/j.na.2008.04.015
Lee E, Lee Y: Multiple positive solutions of singular two point boundary value problems for second order impulsive differential equations. Applied Mathematics and Computation 2004, 158(3):745-759. 10.1016/j.amc.2003.10.013
Zhang X, Ge W: Impulsive boundary value problems involving the one-dimensional p -Laplacian. Nonlinear Analysis. Theory, Methods & Applications 2009, 70(4):1692-1701. 10.1016/j.na.2008.02.052
Feng M, Pang H: A class of three-point boundary-value problems for second-order impulsive integro-differential equations in Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2009, 70(1):64-82. 10.1016/j.na.2007.11.033
Feng M, Xie D: Multiple positive solutions of multi-point boundary value problem for second-order impulsive differential equations. Journal of Computational and Applied Mathematics 2009, 223(1):438-448. 10.1016/j.cam.2008.01.024
Cannon JR: The solution of the heat equation subject to the specification of energy. Quarterly of Applied Mathematics 1963, 21: 155-160.
Ionkin NI: The solution of a certain boundary value problem of the theory of heat conduction with a nonclassical boundary condition. Differential Equations 1977, 13(2):294-304.
Chegis RYu: Numerical solution of a heat conduction problem with an integral condition. Lietuvos Matematikos Rinkinys 1984, 24(4):209-215.
Il'in V, Moiseev E: Nonlocal boundary value problem of the second kind for a Sturm-Liouville operator. Differential Equations 1987, 23: 979-987.
Eloe PW, Ahmad B:Positive solutions of a nonlinear
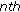 order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521-527. 10.1016/j.aml.2004.05.009
order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521-527. 10.1016/j.aml.2004.05.009Ma R, Wang H: Positive solutions of nonlinear three-point boundary-value problems. Journal of Mathematical Analysis and Applications 2003, 279(1):216-227. 10.1016/S0022-247X(02)00661-3
Ma R, Thompson B: Positive solutions for nonlinear m -point eigenvalue problems. Journal of Mathematical Analysis and Applications 2004, 297(1):24-37. 10.1016/j.jmaa.2003.12.046
Pang C, Dong W, W Z: Green's function and positive solutions of n th order m -point boundary value problem. Applied Mathematics and Computation 2006, 182(2):1231-1239. 10.1016/j.amc.2006.05.010
Yang J, Wei Z: Positive solutions of n th order m -point boundary value problem. Applied Mathematics and Computation 2008, 202(2):715-720. 10.1016/j.amc.2008.03.009
Feng M, Ge W: Existence results for a class of n th order m -point boundary value problems in Banach spaces. Applied Mathematics Letters 2009, 22(8):1303-1308. 10.1016/j.aml.2009.01.047
He X, Ge W: Triple solutions for second-order three-point boundary value problems. Journal of Mathematical Analysis and Applications 2002, 268(1):256-265. 10.1006/jmaa.2001.7824
Guo Y, Ge W: Positive solutions for three-point boundary value problems with dependence on the first order derivative. Journal of Mathematical Analysis and Applications 2004, 290(1):291-301. 10.1016/j.jmaa.2003.09.061
Cheung W, Ren J: Positive solution for m -point boundary value problems. Journal of Mathematical Analysis and Applications 2005, 303(2):565-575. 10.1016/j.jmaa.2004.08.056
Gupta C: A generalized multi-point boundary value problem for second order ordinary differential equations. Applied Mathematics and Computation 1998, 89(1–3):133-146.
Feng W: On an m -point boundary value problem. Nonlinear Analysis. Theory, Methods & Applications 1997, 30(8):5369-5374. 10.1016/S0362-546X(97)00360-X
Feng W, Webb JRL: Solvability of m -point boundary value problems with nonlinear growth. Journal of Mathematical Analysis and Applications 1997, 212(2):467-480. 10.1006/jmaa.1997.5520
Feng W, Webb JRL: Solvability of three point boundary value problems at resonance. Nonlinear Analysis. Theory, Methods & Applications 1997, 30(6):3227-3238. 10.1016/S0362-546X(96)00118-6
Feng M, Ji D, Ge W: Positive solutions for a class of boundary-value problem with integral boundary conditions in Banach spaces. Journal of Computational and Applied Mathematics 2008, 222(2):351-363. 10.1016/j.cam.2007.11.003
Zhang G, Sun J: Positive solutions of m -point boundary value problems. Journal of Mathematical Analysis and Applications 2004, 291(2):406-418. 10.1016/j.jmaa.2003.11.034
Feng M, Ge W: Positive solutions for a class of m -point singular boundary value problems. Mathematical and Computer Modelling 2007, 46(3-4):375-383. 10.1016/j.mcm.2006.11.009
Ahmad B, Nieto JJ: Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions. Boundary Value Problems 2009, 2009: 11.
Webb JRL, Infante G, Franco D: Positive solutions of nonlinear fourth-order boundary-value problems with local and non-local boundary conditions. Proceedings of the Royal Society of Edinburgh 2008, 138(2):427-446.
Zhang X, Liu L: A necessary and sufficient condition for positive solutions for fourth-order multi-point boundary value problems with p -Laplacian. Nonlinear Analysis. Theory, Methods & Applications 2008, 68(10):3127-3137. 10.1016/j.na.2007.03.006
Bai ZB, Ge W: Existence of positive solutions to fourth order quasilinear boundary value problems. Acta Mathematica Sinica 2006, 22(6):1825-1830. 10.1007/s10114-005-0806-z
Bai Z: The upper and lower solution method for some fourth-order boundary value problems. Nonlinear Analysis. Theory, Methods & Applications 2007, 67(6):1704-1709. 10.1016/j.na.2006.08.009
Ma R, Wang H: On the existence of positive solutions of fourth-order ordinary differential equations. Applicable Analysis 1995, 59(1–4):225-231.
Bai Z: Iterative solutions for some fourth-order periodic boundary value problems. Taiwanese Journal of Mathematics 2008, 12(7):1681-1690.
Bai Z: Positive solutions of some nonlocal fourth-order boundary value problem. Applied Mathematics and Computation 2010, 215(12):4191-4197. 10.1016/j.amc.2009.12.040
Liu L, Zhang X, Wu Y: Positive solutions of fourth-order nonlinear singular Sturm-Liouville eigenvalue problems. Journal of Mathematical Analysis and Applications 2007, 326(2):1212-1224. 10.1016/j.jmaa.2006.03.029
Zhang X, Ge W: Positive solutions for a class of boundary-value problems with integral boundary conditions. Computers & Mathematics with Applications 2009, 58(2):203-215. 10.1016/j.camwa.2009.04.002
Guo D, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Acknowledgment
This work is supported by the National Natural Science Foundation of China (10771065), the Natural Sciences Foundation of Heibei Province (A2007001027), the Funding Project for Academic Human Resources Development in Institutions of Higher Learning Under the Jurisdiction of Beijing Municipality (PHR201008430), the Scientific Research Common Program of Beijing Municipal Commission of Education(KM201010772018) and Beijing Municipal Education Commission(71D0911003). The authors thank the referee for his/her careful reading of the paper and useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Feng, M., Zhang, X. & Yang, X. Positive Solutions of  th-Order Nonlinear Impulsive Differential Equation with Nonlocal Boundary Conditions.
Bound Value Probl 2011, 456426 (2011). https://doi.org/10.1155/2011/456426
th-Order Nonlinear Impulsive Differential Equation with Nonlocal Boundary Conditions.
Bound Value Probl 2011, 456426 (2011). https://doi.org/10.1155/2011/456426
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/456426
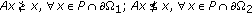 ;
;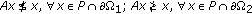 .
.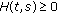 is continuous for all
is continuous for all 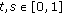 , and
, and 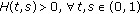 .
. for each
for each  .
.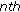 order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521-527. 10.1016/j.aml.2004.05.009
order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521-527. 10.1016/j.aml.2004.05.009