- Research Article
- Open access
- Published:
New Existence Results for Higher-Order Nonlinear Fractional Differential Equation with Integral Boundary Conditions
Boundary Value Problems volume 2011, Article number: 720702 (2011)
Abstract
This paper investigates the existence and multiplicity of positive solutions for a class of higher-order nonlinear fractional differential equations with integral boundary conditions. The results are established by converting the problem into an equivalent integral equation and applying Krasnoselskii's fixed-point theorem in cones. The nonexistence of positive solutions is also studied.
1. Introduction
Fractional differential equations arise in many engineering and scientific disciplines as the mathematical modelling of systems and processes in the fields of physics, chemistry, aerodynamics, electrodynamics of complex medium, polymer rheology, Bode's analysis of feedback amplifiers, capacitor theory, electrical circuits, electron-analytical chemistry, biology, control theory, fitting of experimental data, and so forth, and involves derivatives of fractional order. Fractional derivatives provide an excellent tool for the description of memory and hereditary properties of various materials and processes. This is the main advantage of fractional differential equations in comparison with classical integer-order models. An excellent account in the study of fractional differential equations can be found in [1–5]. For the basic theory and recent development of the subject, we refer a text by Lakshmikantham [6]. For more details and examples, see [7–23] and the references therein. However, the theory of boundary value problems for nonlinear fractional differential equations is still in the initial stages and many aspects of this theory need to be explored.
In [23], Zhang used a fixed-point theorem for the mixed monotone operator to show the existence of positive solutions to the following singular fractional differential equation.

subject to the boundary conditions

where  is the standard Rimann-Liouville fractional derivative of order
is the standard Rimann-Liouville fractional derivative of order  , the nonlinearity
, the nonlinearity  may be singular at
may be singular at  , and function
, and function  may be singular at
may be singular at  . The author derived the corresponding Green's function named by fractional Green's function and obtained some properties as follows.
. The author derived the corresponding Green's function named by fractional Green's function and obtained some properties as follows.
Proposition 1.1.
Green's function  satisfies the following conditions:
satisfies the following conditions:
(i) for all
for all  ;
;
(ii)there exists a positive function  such that
such that

where  and
and

here  .
.
It is well known that the cone theoretic techniques play a very important role in applying Green's function in the study of solutions to boundary value problems. In [23], the author cannot acquire a positive constant taking instead of the role of positive function  with
with  in (1.3). At the same time, we notice that many authors obtained the similar properties to that of (1.3), for example, see Bai [12], Bai and L
in (1.3). At the same time, we notice that many authors obtained the similar properties to that of (1.3), for example, see Bai [12], Bai and L [13], Jiang and Yuan [14], Li et al, [15], Kaufmann and Mboumi [19], and references therein. Naturally, one wishes to find whether there exists a positive constant
[13], Jiang and Yuan [14], Li et al, [15], Kaufmann and Mboumi [19], and references therein. Naturally, one wishes to find whether there exists a positive constant  such that
such that

for the fractional order cases. In Section 2, we will deduce some new properties of Green's function.
Motivated by the above mentioned work, we study the following higher-order singular boundary value problem of fractional differential equation.

where  is the standard Rimann-Liouville fractional derivative of order
is the standard Rimann-Liouville fractional derivative of order  and
and  may be singular at
may be singular at  or/and at
or/and at  ,
,  is nonnegative, and
is nonnegative, and  .
.
For the case of  , the boundary value problems () reduces to the problem studied by Eloe and Ahmad in [24]. In [24], the authors used the Krasnosel'skii and Guo [25] fixed-point theorem to show the existence of at least one positive solution if
, the boundary value problems () reduces to the problem studied by Eloe and Ahmad in [24]. In [24], the authors used the Krasnosel'skii and Guo [25] fixed-point theorem to show the existence of at least one positive solution if  is either superlinear or sublinear to problem (). For the case of
is either superlinear or sublinear to problem (). For the case of  , the boundary value problems () is related to a m-point boundary value problems of integer-order differential equation. Under this case, a great deal of research has been devoted to the existence of solutions for problem (), for example, see Pang et al. [26], Yang and Wei [27], Feng and Ge [28], and references therein. All of these results are based upon the fixed-point index theory, the fixed-point theorems and the fixed-point theory in cone for strict set contraction operator.
, the boundary value problems () is related to a m-point boundary value problems of integer-order differential equation. Under this case, a great deal of research has been devoted to the existence of solutions for problem (), for example, see Pang et al. [26], Yang and Wei [27], Feng and Ge [28], and references therein. All of these results are based upon the fixed-point index theory, the fixed-point theorems and the fixed-point theory in cone for strict set contraction operator.
The organization of this paper is as follows. We will introduce some lemmas and notations in the rest of this section. In Section 2, we present the expression and properties of Green's function associated with boundary value problem (). In Section 3, we discuss some characteristics of the integral operator associated with the problem () and state a fixed-point theorem in cones. In Section 4, we discuss the existence of at least one positive solution of boundary value problem (). In Section 5, we will prove the existence of two or  positive solutions, where
positive solutions, where  is an arbitrary natural number. In Section 6, we study the nonexistence of positive solution of boundary value problem (). In Section 7, one example is also included to illustrate the main results. Finally, conclusions in Section 8 close the paper.
is an arbitrary natural number. In Section 6, we study the nonexistence of positive solution of boundary value problem (). In Section 7, one example is also included to illustrate the main results. Finally, conclusions in Section 8 close the paper.
The fractional differential equations related notations adopted in this paper can be found, if not explained specifically, in almost all literature related to fractional differential equations. The readers who are unfamiliar with this area can consult, for example, [1–6] for details.
Definition 1.2 (see [4]).
The integral

where  , is called Riemann-Liouville fractional integral of order
, is called Riemann-Liouville fractional integral of order  .
.
Definition 1.3 (see [4]).
For a function  given in the interval
given in the interval  , the expression
, the expression

where  denotes the integer part of number
denotes the integer part of number  , is called the Riemann-Liouville fractional derivative of order
, is called the Riemann-Liouville fractional derivative of order  .
.
Lemma 1.4 (see [13]).
Assume that  with a fractional derivative of order
with a fractional derivative of order  that belongs to
that belongs to  . Then
. Then

for some  , where
, where  is the smallest integer greater than or equal to
is the smallest integer greater than or equal to  .
.
2. Expression and Properties of Green's Function
In this section, we present the expression and properties of Green's function associated with boundary value problem ().
Lemma 2.1.
Assume that  Then for any
Then for any  , the unique solution of boundary value problem
, the unique solution of boundary value problem

is given by

where



Proof.
By Lemma 1.4, we can reduce the equation of problem (2.1) to an equivalent integral equation

By  , there is
, there is  . Thus,
. Thus,

Differentiating (2.7), we have

By (2.8) and  we have
we have  Similarly, we can obtain that
Similarly, we can obtain that  Then
Then

By  , we have
, we have

Therefore, the unique solution of BVP (2.1) is

where  is defined by (2.4).
is defined by (2.4).
From (2.11), we have

It follows that

Substituting (2.13) into (2.11), we obtain

where  and
and  are defined by (2.3), (2.4), and (2.5), respectively. The proof is complete.
are defined by (2.3), (2.4), and (2.5), respectively. The proof is complete.
From (2.3), (2.4), and (2.5), we can prove that  and
and  have the following properties.
have the following properties.
Proposition 2.2.
The function  defined by (2.4) satisfies
defined by (2.4) satisfies
(i) is continuous for all
is continuous for all  ;
;
(ii)for all  , one has
, one has

where

Proof.
-
(i)
It is obvious that
 is continuous on
is continuous on 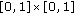 and
and 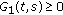 when
when  .
.
For  , we have
, we have

So, by (2.4), we have

Similarly, for  , we have
, we have  .
.
-
(ii)
Since
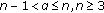 , it is clear that
, it is clear that  is increasing with respect to
is increasing with respect to 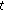 for
for 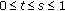 .
.
On the other hand, from the definition of  , for given
, for given  , we have
, we have

Let

Then, we have

and so,

Noticing  , from (2.22), we have
, from (2.22), we have

Then, for given  , we have
, we have  arrives at maximum at
arrives at maximum at  when
when  . This together with the fact that
. This together with the fact that  is increasing on
is increasing on  , we obtain that (2.15) holds.
, we obtain that (2.15) holds.
Remark 2.3.
From Figure 1, we can see that  for
for  . If
. If  , then
, then

Remark 2.4.
From Figure 2, we can see that  is increasing with respect to
is increasing with respect to  .
.
Remark 2.5.
From Figure 3, we can see that  for
for  , where
, where  .
.
Remark 2.6.
Let  . From (2.15), for
. From (2.15), for  , we have
, we have

Remark 2.7.
From (2.25), we have

Remark 2.8.
From Figure 4, it is easy to obtain that  is decreasing with respect to
is decreasing with respect to  , and
, and

Proposition 2.9.
There exists  such that
such that

Proof.
For  , we divide the proof into the following three cases for
, we divide the proof into the following three cases for  .
.
Case 1.
If  , then from (i) of Proposition 2.2 and Remark 2.5, we have
, then from (i) of Proposition 2.2 and Remark 2.5, we have

It is obvious that  and
and  are bounded on
are bounded on  . So, there exists a constant
. So, there exists a constant  such that
such that

Case 2.
If  , then from (2.4), we have
, then from (2.4), we have

On the other hand, from the definition of  , we obtain that
, we obtain that  takes its maximum
takes its maximum  at
at  . So
. So

Therefore,  . Letting
. Letting  , we have
, we have

Case 3.
If  , from (i) of Proposition 2.2, it is clear that
, from (i) of Proposition 2.2, it is clear that

In view of Remarks 2.6–2.8, we have

From (2.35), there exists a constant  such that
such that

Letting  and using (2.30), (2.33), and (2.36), it follows that (2.28) holds. This completes the proof.
and using (2.30), (2.33), and (2.36), it follows that (2.28) holds. This completes the proof.
Let

Proposition 2.10.
If  , then one has
, then one has
(i) is continuous for all
is continuous for all  ;
;
(ii) .
.
Proof.
Using the properties of  , definition of
, definition of  , it can easily be shown that (i) and (ii) hold.
, it can easily be shown that (i) and (ii) hold.
Theorem 2.11.
If  , the function
, the function  defined by (2.3) satisfies
defined by (2.3) satisfies
(i) is continuous for all
is continuous for all  ;
;
(ii) for each
for each  , and
, and

where

 is defined by (2.16),
is defined by (2.16),  is defined in Proposition 2.9.
is defined in Proposition 2.9.
Proof.
-
(i)
From Propositions 2.2 and 2.10, we obtain that
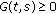 is continuous for all
is continuous for all 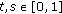 , and
, and 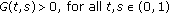 .
. -
(ii)
From (ii) of Proposition 2.2 and (ii) of Proposition 2.10, we have that
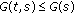 for each
for each 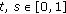 .
.
Now, we show that (2.38) holds.
In fact, from Proposition 2.9, we have

Then the proof of Theorem 2.11 is completed.
Remark 2.12.
From the definition of  , it is clear that
, it is clear that  .
.
3. Preliminaries
Let  and
and  denote a real Banach space with the norm
denote a real Banach space with the norm  defined by
defined by  Let
Let

To prove the existence of positive solutions for the boundary value problem (), we need the following assumptions:
() on any subinterval of (0,1) and
on any subinterval of (0,1) and  , where
, where  is defined in Theorem 2.11;
is defined in Theorem 2.11;
() and
and  uniformly with respect to
uniformly with respect to  on
on  ;
;
() , where
, where  is defined by (2.37).
is defined by (2.37).
From condition  , it is not difficult to see that
, it is not difficult to see that  may be singular at
may be singular at  or/and at
or/and at  , that is,
, that is,  or/and
or/and  .
.
Define  by
by

where  is defined by (2.3).
is defined by (2.3).
Lemma 3.1.
Let  hold. Then boundary value problems () has a solution
hold. Then boundary value problems () has a solution  if and only if
if and only if  is a fixed point of
is a fixed point of  .
.
Proof.
From Lemma 2.1, we can prove the result of this lemma.
Lemma 3.2.
Let  hold. Then
hold. Then  and
and  is completely continuous.
is completely continuous.
Proof.
For any  , by (3.2), we can obtain that
, by (3.2), we can obtain that  . On the other hand, by (ii) of Theorem 2.11, we have
. On the other hand, by (ii) of Theorem 2.11, we have

Similarly, by (2.38), we obtain

So,  and hence
and hence  . Next by similar proof of Lemma
. Next by similar proof of Lemma  in [13] and Ascoli-Arzela theorem one can prove
in [13] and Ascoli-Arzela theorem one can prove  is completely continuous. So it is omitted.
is completely continuous. So it is omitted.
To obtain positive solutions of boundary value problem (), the following fixed-point theorem in cones is fundamental which can be found in [25, page 94].
Lemma 3.3 (Fixed-point theorem of cone expansion and compression of norm type).
Let  be a cone of real Banach space
be a cone of real Banach space  , and let
, and let  and
and  be two bounded open sets in
be two bounded open sets in  such that
such that  and
and  . Let operator
. Let operator  be completely continuous. Suppose that one of the two conditions
be completely continuous. Suppose that one of the two conditions
(i) and
and 
or
(ii) and
and 
is satisfied. Then  has at least one fixed point in
has at least one fixed point in  .
.
4. Existence of Positive Solution
In this section, we impose growth conditions on  which allow us to apply Lemma 3.3 to establish the existence of one positive solution of boundary value problem (), and we begin by introducing some notations:
which allow us to apply Lemma 3.3 to establish the existence of one positive solution of boundary value problem (), and we begin by introducing some notations:

where  denotes
denotes  or
or  and
and

Theorem 4.1.
Assume that  hold. In addition, one supposes that one of the following conditions is satisfied:
hold. In addition, one supposes that one of the following conditions is satisfied:
 and
and  (particularly,
(particularly,  and
and  ).
).
there exist two constants  with
with  such that
such that  is nondecreasing on
is nondecreasing on 
for all  , and
, and  , and
, and  for all
for all  . Then boundary value problem () has at least one positive solution.
. Then boundary value problem () has at least one positive solution.
Proof.
Let  be cone preserving completely continuous that is defined by (3.2).
be cone preserving completely continuous that is defined by (3.2).
Case 1.
The condition  holds. Considering
holds. Considering  , there exists
, there exists  such that
such that  , for
, for  , where
, where  satisfies
satisfies  . Then, for
. Then, for  , we have
, we have

that is,  imply that
imply that

Next, turning to  , there exists
, there exists  such that
such that

where  satisfies
satisfies  .
.
Set

then  .
.
Chose  . Then, for
. Then, for  , we have
, we have

that is,  imply that
imply that

Case 2.
The Condition  satisfies. For
satisfies. For  , from (3.1) we obtain that
, from (3.1) we obtain that  . Therefore, for
. Therefore, for  , we have
, we have  for
for  , this together with
, this together with  , we have
, we have

that is,  imply that
imply that

On the other hand, for  , we have that
, we have that  for
for  , this together with
, this together with  , we have
, we have

that is,  imply that
imply that

Applying Lemma 3.3 to (4.4) and (4.8), or (4.10) and (4.12), yields that  has a fixed point
has a fixed point  or
or  with
with  . Thus it follows that boundary value problems () has a positive solution
. Thus it follows that boundary value problems () has a positive solution  , and the theorem is proved.
, and the theorem is proved.
Theorem 4.2.
Assume that  hold. In addition, one supposes that the following condition is satisfied:
hold. In addition, one supposes that the following condition is satisfied:
 and
and  (particularly,
(particularly,  and
and  ).
).
Then boundary value problem () has at least one positive solution.
5. The Existence of Multiple Positive Solutions
Now we discuss the multiplicity of positive solutions for boundary value problem (). We obtain the following existence results.
Theorem 5.1.
Assume  , and the following two conditions:
, and the following two conditions:
 and
and  (particularly,
(particularly,  );
);
there exists  such that
such that 
Then boundary value problem () has at least two positive solutions  , which satisfy
, which satisfy

Proof.
We consider condition  . Choose
. Choose  with
with  .
.
If  , then by the proof of (4.4), we have
, then by the proof of (4.4), we have

If  , then similar to the proof of (4.4), we have
, then similar to the proof of (4.4), we have

On the other hand, by  , for
, for  we have
we have

By (5.4), we have

Applying Lemma 3.3 to (5.2), (5.3), and (5.5) yields that  has a fixed point
has a fixed point  , and a fixed point
, and a fixed point  Thus it follows that boundary value problem () has at least two positive solutions
Thus it follows that boundary value problem () has at least two positive solutions  and
and  . Noticing (5.5), we have
. Noticing (5.5), we have  and
and  . Therefore (5.1) holds, and the proof is complete.
. Therefore (5.1) holds, and the proof is complete.
Theorem 5.2.
Assume  , and the following two conditions:
, and the following two conditions:
 and
and  ;
;
there exists  such that
such that 
Then boundary value problem () has at least two positive solutions  , which satisfy
, which satisfy

Theorem 5.3.
Assume that  ,
,  and
and  hold. If there exist
hold. If there exist  positive numbers
positive numbers  with
with  such that
such that
 for
for  and
and  for
for 
Then boundary value problem () has at least  positive solutions
positive solutions  satisfying
satisfying 
Theorem 5.4.
Assume that  ,
,  and
and  hold. If there exist
hold. If there exist  positive numbers
positive numbers  with
with  such that
such that
 is nondecreasing on
is nondecreasing on  for all
for all  ;
;
 , and
, and 
Then boundary value problem () has at least  positive solutions
positive solutions  satisfying
satisfying 
6. The Nonexistence of Positive Solution
Our last results corresponds to the case when boundary value problem () has no positive solution.
Theorem 6.1.
Assume  and
and  , then boundary value problem () has no positive solution.
, then boundary value problem () has no positive solution.
Proof.
Assume to the contrary that  is a positive solution of the boundary value problem (). Then,
is a positive solution of the boundary value problem (). Then, , and
, and

which is a contradiction, and complete the proof.
Similarly, we have the following results.
Theorem 6.2.
Assume  and
and  , then boundary value problem () has no positive solution.
, then boundary value problem () has no positive solution.
7. Example
To illustrate how our main results can be used in practice we present an example.
Example 7.1.
Consider the following boundary value problem of nonlinear fractional differential equations:

where

It is easy to see that  hold. By simple computation, we have
hold. By simple computation, we have

thus it follows that problem (7.1) has a positive solution by  .
.
8. Conclusions
In this paper, by using the famous Guo-Krasnoselskii fixed-point theorem, we have investigated the existence and multiplicity of positive solutions for a class of higher-order nonlinear fractional differential equations with integral boundary conditions and obtained some easily verifiable sufficient criteria. The interesting point is that we obtain some new positive properties of Green's function, which significantly extend and improve many known results for fractional order cases, for example, see [12–15, 19]. The methodology which we employed in studying the boundary value problems of integer-order differential equation in [28] can be modified to establish similar sufficient criteria for higher-order nonlinear fractional differential equations. It is worth mentioning that there are still many problems that remain open in this vital field except for the results obtained in this paper: for example, whether or not we can obtain the similar results of fractional differential equations with p-Laplace operator by employing the same technique of this paper, and whether or not our concise criteria can guarantee the existence of positive solutions for higher-order nonlinear fractional differential equations with impulses. More efforts are still needed in the future.
References
Miller KS, Ross B: An Introduction to the Fractional Calculus and Fractional Differential Equations, A Wiley-Interscience Publication. John Wiley & Sons, New York, NY, USA; 1993:xvi+366.
Oldham KB, Spanier J: The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order, Mathematics in Science and Engineering. Volume 11. Academic Press, London, UK; 1974:xiii+234.
Podlubny I: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, Mathematics in Science and Engineering. Volume 198. Academic Press, San Diego, Calif, USA; 1999:xxiv+340.
Samko SG, Kilbas AA, Marichev OI: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, Yverdon, Switzerland; 1993:xxxvi+976.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies. Volume 204. Elsevier, Amsterdam, The Netherlands; 2006.
Lakshmikantham V, Leela S, Vasundhara Devi J: Theory of Fractional Dynamic Systems. Cambridge Academic, Cambridge, UK; 2009.
Lakshmikantham V, Vatsala AS: Basic theory of fractional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(8):2677-2682. 10.1016/j.na.2007.08.042
Lakshmikantham V: Theory of fractional functional differential equations. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(10):3337-3343. 10.1016/j.na.2007.09.025
Lakshmikantham V, Vatsala AS: General uniqueness and monotone iterative technique for fractional differential equations. Applied Mathematics Letters 2008, 21(8):828-834. 10.1016/j.aml.2007.09.006
Ahmad B, Nieto JJ: Existence of solutions for nonlocal boundary value problems of higher-order nonlinear fractional differential equations. Abstract and Applied Analysis 2009, 2009:-9.
Ahmad B, Nieto JJ: Existence results for nonlinear boundary value problems of fractional integrodifferential equations with integral boundary conditions. Boundary Value Problems 2009, 2009:-11.
Bai Z: On positive solutions of a nonlocal fractional boundary value problem. Nonlinear Analysis: Theory, Methods & Applications 2010, 72(2):916-924. 10.1016/j.na.2009.07.033
Bai Z, Lü H: Positive solutions for boundary value problem of nonlinear fractional differential equation. Journal of Mathematical Analysis and Applications 2005, 311(2):495-505. 10.1016/j.jmaa.2005.02.052
Jiang D, Yuan C: The positive properties of the Green function for Dirichlet-type boundary value problems of nonlinear fractional differential equations and its application. Nonlinear Analysis: Theory, Methods and Applications 2009, 72(2):710-719.
Li CF, Luo XN, Zhou Y: Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations. Computers and Mathematics with Applications 2010, 59(3):1363-1375. 10.1016/j.camwa.2009.06.029
Benchohra M, Hamani S, Ntouyas SK: Boundary value problems for differential equations with fractional order and nonlocal conditions. Nonlinear Analysis: Theory, Methods and Applications 2009, 71(7-8):2391-2396. 10.1016/j.na.2009.01.073
Salem HAH: On the nonlinear Hammerstein integral equations in Banach spaces and application to the boundary value problem of fractional order. Mathematical and Computer Modelling 2008, 48(7-8):1178-1190. 10.1016/j.mcm.2007.12.015
Salem HAH: On the fractional order m -point boundary value problem in reflexive Banach spaces and weak topologies. Journal of Computational and Applied Mathematics 2009, 224(2):565-572. 10.1016/j.cam.2008.05.033
Kaufmann ER, Mboumi E: Positive solutions of a boundary value problem for a nonlinear fractional differential equation. Electronic Journal of Qualitative Theory of Differential Equations 2008, 2008(3):1-11.
Zhang S: Positive solutions for boundary-value problems of nonlinear fractional differential equations. Electronic Journal of Differential Equations 2006, 2006: 1-12.
Zhang S: The existence of a positive solution for a nonlinear fractional differential equation. Journal of Mathematical Analysis and Applications 2000, 252(2):804-812. 10.1006/jmaa.2000.7123
Zhang S: Existence of positive solution for some class of nonlinear fractional differential equations. Journal of Mathematical Analysis and Applications 2003, 278(1):136-148. 10.1016/S0022-247X(02)00583-8
Zhang S: Positive solutions to singular boundary value problem for nonlinear fractional differential equation. Computers and Mathematics with Applications 2010, 59(3):1300-1309. 10.1016/j.camwa.2009.06.034
Eloe PW, Ahmad B: Positive solutions of a nonlinear n th order boundary value problem with nonlocal conditions. Applied Mathematics Letters 2005, 18(5):521-527. 10.1016/j.aml.2004.05.009
Guo D, Lakshmikantham V, Liu X: Nonlinear Integral Equations in Abstract Spaces, Mathematics and Its Applications. Volume 373. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1996:viii+341.
Pang C, Dong W, Wei Z: Green's function and positive solutions of n th order m -point boundary value problem. Applied Mathematics and Computation 2006, 182(2):1231-1239. 10.1016/j.amc.2006.05.010
Yang J, Wei Z: Positive solutions of n th order m -point boundary value problem. Applied Mathematics and Computation 2008, 202(2):715-720. 10.1016/j.amc.2008.03.009
Feng M, Ge W: Existence results for a class of n th order m -point boundary value problems in Banach spaces. Applied Mathematics Letters 2009, 22(8):1303-1308. 10.1016/j.aml.2009.01.047
Acknowledgments
The authors thank the referee for his/her careful reading of the manuscript and useful suggestions. These have greatly improved this paper. This work is sponsored by the Funding Project for Academic Human Resources Development in Institutions of Higher Learning Under the Jurisdiction of Beijing Municipality (PHR201008430), the Scientific Research Common Program of Beijing Municipal Commission of Education (KM201010772018), the 2010 level of scientific research of improving project (5028123900), the Graduate Technology Innovation Project (5028211000) and Beijing Municipal Education Commission (71D0911003).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Feng, M., Zhang, X. & Ge, W. New Existence Results for Higher-Order Nonlinear Fractional Differential Equation with Integral Boundary Conditions. Bound Value Probl 2011, 720702 (2011). https://doi.org/10.1155/2011/720702
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/720702
 is continuous on
is continuous on 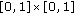 and
and 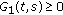 when
when  .
.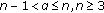 , it is clear that
, it is clear that  is increasing with respect to
is increasing with respect to 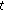 for
for 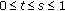 .
.

 for
for  .
.
 for
for
 .
.

 for
for
 ,
,
 .
.

 for
for
 .
.
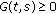 is continuous for all
is continuous for all 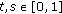 , and
, and 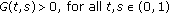 .
.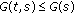 for each
for each 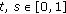 .
.