- Research Article
- Open access
- Published:
Hierarchies of Difference Boundary Value Problems
Boundary Value Problems volume 2011, Article number: 743135 (2011)
Abstract
This paper generalises the work done in Currie and Love (2010), where we studied the effect of applying two Crum-type transformations to a weighted second-order difference equation with various combinations of Dirichlet, non-Dirichlet, and affine  -dependent boundary conditions at the end points, where
-dependent boundary conditions at the end points, where  is the eigenparameter. We now consider general
is the eigenparameter. We now consider general  -dependent boundary conditions. In particular we show, using one of the Crum-type transformations, that it is possible to go up and down a hierarchy of boundary value problems keeping the form of the second-order difference equation constant but possibly increasing or decreasing the dependence on
-dependent boundary conditions. In particular we show, using one of the Crum-type transformations, that it is possible to go up and down a hierarchy of boundary value problems keeping the form of the second-order difference equation constant but possibly increasing or decreasing the dependence on  of the boundary conditions at each step. In addition, we show that the transformed boundary value problem either gains or loses an eigenvalue, or the number of eigenvalues remains the same as we step up or down the hierarchy.
of the boundary conditions at each step. In addition, we show that the transformed boundary value problem either gains or loses an eigenvalue, or the number of eigenvalues remains the same as we step up or down the hierarchy.
1. Introduction
Our interest in this topic arose from the work done on transformations and factorisations of continuous Sturm-Liouville boundary value problems by Binding et al. [1] and Browne and Nillsen [2], notably. We make use of analogous ideas to those discussed in [3–5] to study difference equations in order to contribute to the development of the theory of discrete spectral problems.
Numerous efforts to develop hierarchies exist in the literature, however, they are not specifically aimed at difference equations per se and generally not for three-term recurrence relations. Ding et al., [6], derived a hierarchy of nonlinear differential-difference equations by starting with a two-parameter discrete spectral problem, as did Luo and Fan [7], whose hierarchy possessed bi-Hamiltonian structures. Clarkson et al.'s, [8], interest in hierarchies lay in the derivation of infinite sequences of systems of difference equations by using the B cklund transformation for the equations in the second Painlev
cklund transformation for the equations in the second Painlev equation hierarchy. Wu and Geng, [9], showed early on that the hierarchy of differential-difference equations possesses Hamiltonian structures while a Darboux transformation for the discrete spectral problem is shown to exist.
equation hierarchy. Wu and Geng, [9], showed early on that the hierarchy of differential-difference equations possesses Hamiltonian structures while a Darboux transformation for the discrete spectral problem is shown to exist.
In this paper, we consider a weighted second-order difference equation of the form

where  represents a weight function and
represents a weight function and  a potential function.
a potential function.
Our aim is to extend the results obtained in [10, 11] by establishing a hierarchy of difference boundary value problems. A key tool in our analysis will be the Crum-type transformation (2.1). In [10], it was shown that (2.1) leaves the form of the difference equation (1.1) unchanged. For us, the effect of (2.1) on the boundary conditions will be crucial. We consider  (eigenparameter)-dependent boundary conditions at the end points. In particular, the eigenparameter dependence at the initial end point will be given by a positive Nevanlinna function,
(eigenparameter)-dependent boundary conditions at the end points. In particular, the eigenparameter dependence at the initial end point will be given by a positive Nevanlinna function,  say, and at the terminal end point by a negative Nevanlinna function,
say, and at the terminal end point by a negative Nevanlinna function,  say. The case of
say. The case of  was covered in [10] and the the case of
was covered in [10] and the the case of  constant was studied in [11]. Applying transformation (2.1) to the boundary conditions results in a so-called transformed boundary value problem, where either the new boundary conditions have more
constant was studied in [11]. Applying transformation (2.1) to the boundary conditions results in a so-called transformed boundary value problem, where either the new boundary conditions have more  -dependence, less
-dependence, less  -dependence, or the same amount of
-dependence, or the same amount of  -dependence as the original boundary conditions. Consequently the transformed boundary value problem has either one more eigenvalue, one less eigenvalue, or the same number of eigenvalues as the original boundary value problem. Thus, it is possible to construct a chain, or hierarchy, of difference boundary value problems where the successive links in the chain are obtained by applying the variations of (2.1) given in this paper. For instance, it is possible to go from a boundary value problem with
-dependence as the original boundary conditions. Consequently the transformed boundary value problem has either one more eigenvalue, one less eigenvalue, or the same number of eigenvalues as the original boundary value problem. Thus, it is possible to construct a chain, or hierarchy, of difference boundary value problems where the successive links in the chain are obtained by applying the variations of (2.1) given in this paper. For instance, it is possible to go from a boundary value problem with  -dependent boundary conditions to a boundary value problem with
-dependent boundary conditions to a boundary value problem with  -independent boundary conditions or vice versa simply by applying the correct variation of (2.1) an appropriate number of times. Moreover, at each step, we can precisely track the eigenvalues that have been lost or gained. Hence, this paper provides a significant development in the theory of three-term difference boundary value problems in regard to singularities and asymptotics in the hierarchy structure. For similar results in the continuous case, see [12].
-independent boundary conditions or vice versa simply by applying the correct variation of (2.1) an appropriate number of times. Moreover, at each step, we can precisely track the eigenvalues that have been lost or gained. Hence, this paper provides a significant development in the theory of three-term difference boundary value problems in regard to singularities and asymptotics in the hierarchy structure. For similar results in the continuous case, see [12].
There is an obvious connection between the three-term difference equation and orthogonal polynomials. In fact, the three-term recurrence relation satisfied by orthogonal polynomials is perhaps the most important information for the constructive and computational use of orthogonal polynomials [13].
Difference equations and operators and results concerning their existence and construction of their solutions have been discussed in [14, 15]. Difference equations arise in numerous settings and have applications in diverse areas such as quantum field theory, combinatorics, mathematical physics and biology, dynamical systems, economics, statistics, electrical circuit analysis, computer visualization, and many other fields. They are especially useful where recursive computations are required. In particular see [16] [9, Introduction] for three physical applications of the difference equation (1.1), namely, the vibrating string, electrical network theory and Markov processes, in birth and death processes and random walks.
It should be noted that G. Teschl's work, [17, Chapter 11], on spectral and inverse spectral theory of Jacobi operators, provides an alternative factorisation, to that of [10], of a second-order difference equation, where the factors are adjoints of one another.
This paper is structured as follows.
In Section 2, all the necsessary results from [10] are recalled, in particular how (1.1) transforms under (2.1). In addition, we also recap some important properties of Nevanlinna functions.
The focus of Section 3 is to show exactly the effect that (2.1) has on boundary conditions of the form

We give explicitly the new boundary conditions which are obeyed, from which it can be seen whether the  -dependence has increased, decreased, or remained the same.
-dependence has increased, decreased, or remained the same.
Lastly, in Section 4, we compare the spectrum of the original boundary value problem with that of the transformed boundary value problem and show under which conditions the transformed boundary value problem has one more eigenvalue, one less eigenvalue, or the same number of eigenvalues as the original boundary value problem.
2. Preliminaries
In [10], we considered (1.1) for  , where the values of
, where the values of  and
and  are given by boundary conditions, that is,
are given by boundary conditions, that is,  is defined for
is defined for  .
.
Let the mapping  be defined by
be defined by

where, throughout this paper,  is a solution to (1.1) for
is a solution to (1.1) for  such that
such that  for all
for all  . Whether or not
. Whether or not  obeys the various given boundary conditions (to be specified later) is of vital importance in obtaining the results that follow.
obeys the various given boundary conditions (to be specified later) is of vital importance in obtaining the results that follow.
From [10], we have the following theorem.
Theorem 2.1.
Under the mapping (2.1), (1.1) transforms to

where for 

We now recall some properties of Nevanlinna functions.
-
(I)
The inverse of a positive Nevanlinna function is a negative Nevanlinna function, that is
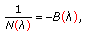 (2.4)
(2.4)
where  are positive Nevanlinna functions. This follows directly from the fact that
are positive Nevanlinna functions. This follows directly from the fact that  if and only if
if and only if  .
.
-
(II)
If
 (2.5)
(2.5)
then

This follows by (I) together with the fact that since  has
has  zeros
zeros  has
has  poles. Also
poles. Also  as
as  so
so  as
as  . Thus, if
. Thus, if  is a positive Nevanlinna function of the form (2.5), then for
is a positive Nevanlinna function of the form (2.5), then for  ,
,  is a negative Nevanlinna function of the same form.
is a negative Nevanlinna function of the same form.
-
(III)
If
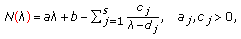 (2.7)
(2.7)
then

since  has
has  zeros so
zeros so  has
has  poles and
poles and  as
as  so
so  as
as  .
.
For the remainder of the paper,  will denote a Nevanlinna function where
will denote a Nevanlinna function where
 is the number of terms in the sum;
is the number of terms in the sum;
 indicates the value of
indicates the value of  at which the boundary condition is imposed and
at which the boundary condition is imposed and

3. General  -Dependent Boundary Conditions
-Dependent Boundary Conditions
In this section, we show how  obeying general
obeying general  -dependent boundary conditions transforms, under (2.1), to
-dependent boundary conditions transforms, under (2.1), to  obeying various types of
obeying various types of  -dependent boundary conditions. The exact form of these boundary conditions is obtained by considering the number of zeros and poles (singularities) of the various Nevanlinna functions under discussion and these correlations are illustrated in the different graphs depicted in this section.
-dependent boundary conditions. The exact form of these boundary conditions is obtained by considering the number of zeros and poles (singularities) of the various Nevanlinna functions under discussion and these correlations are illustrated in the different graphs depicted in this section.
Lemma 3.1.
If  obeys the boundary condition
obeys the boundary condition

then the domain of  may be extended from
may be extended from  to
to  by forcing the condition
by forcing the condition

where

with  .
.
Proof.
The transformed equation (2.2), for  , together with (3.2) gives
, together with (3.2) gives

Also the mapping (2.1), together with (3.1), yields

Substituting (3.5) into (3.4), we obtain

Now (2.1), with  , gives
, gives

which when substituted into (3.6) and dividing through by  results in
results in

This may be rewritten as

Using (1.1), with  , together with (3.1), gives
, together with (3.1), gives

Subtracting (3.10) from (3.9) results in

Rearranging the above equation and dividing through by  yields
yields

and hence

Thus  obeys the equation on the extended domain.
obeys the equation on the extended domain.
The remainder of this section illustrates why it is so important to distinguish between the two cases of  obeying or not obeying the boundary conditions.
obeying or not obeying the boundary conditions.
Theorem 3.2.
Consider  obeying the boundary condition (3.1) where
obeying the boundary condition (3.1) where  is a positive Nevanlinna function, that is,
is a positive Nevanlinna function, that is,  for
for  . Under the mapping (2.1),
. Under the mapping (2.1),  obeying (3.1) transforms to
obeying (3.1) transforms to  obeying (3.2) as follows.
obeying (3.2) as follows.
If  does not obey (3.1) then
does not obey (3.1) then  obeys
obeys


If  does obey (3.1) for
does obey (3.1) for  then
then  obeys
obeys


where  , that is,
, that is,  are positive Nevanlinna functions.
are positive Nevanlinna functions.
In (A) and (B),  is not possible.
is not possible.
Proof.
The fact that  is by construction, see Lemma 3.1. We now examine the form of
is by construction, see Lemma 3.1. We now examine the form of  in Lemma 3.1. Let
in Lemma 3.1. Let  ,
,  ,
,  and
and  then
then

But

thus

Now  has the expansion
has the expansion

where  and the
and the  's correspond to where
's correspond to where  , that is, the singularities of (3.20).
, that is, the singularities of (3.20).
Since  is a positive Nevanlinna function it has a graph of the form shown in Figure 1.
is a positive Nevanlinna function it has a graph of the form shown in Figure 1.
Clearly, the gradient of  at
at  is positive for all
is positive for all  , that is,
, that is,

If  does not obey (3.1), then the zeros of
does not obey (3.1), then the zeros of

are the poles of  , that is, the
, that is, the  's and
's and  where
where  for
for  . It is evident, from Figure 1, that the number of
. It is evident, from Figure 1, that the number of  's is equal to the number of
's is equal to the number of  's, thus in (3.21),
's, thus in (3.21),  .
.
We now examine the form of  in (3.21). As
in (3.21). As  it follows that
it follows that  . Thus
. Thus

Therefore

Hence, substituting into (3.20) gives

Let

Then since  ,
,  and
and  we have that
we have that  and clearly if
and clearly if  then
then  giving (3.14), that is,
giving (3.14), that is,

If  then we want
then we want  so that we have a positive Nevanlinna function, that is
so that we have a positive Nevanlinna function, that is

which means that either,

giving that, since  ,
,

which is as shown in Figure 1, or,

giving that

but this means that  which is not possible.
which is not possible.
Thus,  for
for  , that is, given
, that is, given  , the ratio
, the ratio  must be chosen suitably to ensure that
must be chosen suitably to ensure that  is a positive Nevanlinna function as required. Hence we obtain (3.15), that is
is a positive Nevanlinna function as required. Hence we obtain (3.15), that is

If  obeys (3.1), for
obeys (3.1), for  , then
, then  . Thus in Figure 1, one of the
. Thus in Figure 1, one of the  's
's  is equal to
is equal to  and since
and since  is less than the least eigenvalue of the boundary value problem (1.1), (3.1) together with a boundary condition at
is less than the least eigenvalue of the boundary value problem (1.1), (3.1) together with a boundary condition at  (specified later) it follows that
(specified later) it follows that  , as
, as  for all
for all  .
.
Now

and as 

Thus  is a removable singularity. Alternatively,
is a removable singularity. Alternatively,

which illustrates that the singularity at  is removable.
is removable.
We now have that the number of nonremovable singularities,  , in (3.20) is one less than the number of
, in (3.20) is one less than the number of  's
's  , see Figure 1. Thus (3.21) becomes
, see Figure 1. Thus (3.21) becomes

which may be rewritten as

where  ,
,  for
for  .
.
We now examine the form of  in (3.39). As
in (3.39). As  , we have that, as before,
, we have that, as before,  . Thus
. Thus

Hence, from (3.20),

Let

Then since  ,
,  and
and  we have that
we have that  and clearly if
and clearly if  then
then  giving (3.16), that is,
giving (3.16), that is,

If  then we need
then we need  so that we have a positive Nevanlinna function, that is
so that we have a positive Nevanlinna function, that is

which means that either

giving that, since  ,
,

which is as shown in Figure 1, or,

giving that

but this means that  which is not possible.
which is not possible.
Thus,  for
for  , that is, given
, that is, given  , the ratio
, the ratio  must be chosen suitably to ensure that
must be chosen suitably to ensure that  is a positive Nevanlinna function as required. Hence, we obtain (3.17), that is,
is a positive Nevanlinna function as required. Hence, we obtain (3.17), that is,

In the theorem below, we increase the  dependence by introducing a nonzero
dependence by introducing a nonzero  term in the original boundary condition. As in Theorem 3.2, the
term in the original boundary condition. As in Theorem 3.2, the  dependence of the transformed boundary condition depends on whether or not
dependence of the transformed boundary condition depends on whether or not  obeys the given boundary condition. In addition, to ensure that the
obeys the given boundary condition. In addition, to ensure that the  dependence of the transformed boundary condition is given by a positive Nevanlinna function it is necessary that the transformed boundary condition is imposed at 0 and 1 as opposed to −1 and 0. Thus the interval under consideration shrinks by one unit at the initial end point. By routine calculation it can be shown that the form of the
dependence of the transformed boundary condition is given by a positive Nevanlinna function it is necessary that the transformed boundary condition is imposed at 0 and 1 as opposed to −1 and 0. Thus the interval under consideration shrinks by one unit at the initial end point. By routine calculation it can be shown that the form of the  dependence of the transformed boundary condition, if imposed at −1 and 0, is neither a positive Nevalinna function nor a negative Nevanlinna function.
dependence of the transformed boundary condition, if imposed at −1 and 0, is neither a positive Nevalinna function nor a negative Nevanlinna function.
Theorem 3.3.
Consider  obeying the boundary condition
obeying the boundary condition

where  is a positive Nevanlinna function, that is,
is a positive Nevanlinna function, that is,  and
and  for
for  . Under the mapping (2.1),
. Under the mapping (2.1),  obeying (3.50) transforms to
obeying (3.50) transforms to  obeying the following.
obeying the following.
(1) If  does not obey (3.50) then
does not obey (3.50) then  obeys
obeys

(2) If  does obey (3.50), for
does obey (3.50), for  , then
, then  obeys
obeys

where  .
.
Proof.
Since  and
and  are defined we do not need to extend the domain in order to impose the boundary conditions (3.51) or (3.52).
are defined we do not need to extend the domain in order to impose the boundary conditions (3.51) or (3.52).
The mapping (2.1), at  , together with (3.50) gives
, together with (3.50) gives

Also (2.1), at  , is
, is

Substituting in for  from (1.1), with
from (1.1), with  , and using (3.50), we obtain that
, and using (3.50), we obtain that

From (3.53) and (3.55), it now follows that

As in Theorem 3.2, let  and
and  . Then (3.56) becomes
. Then (3.56) becomes

From Theorem 3.2, we have that  so
so

Also, as in Theorem 3.2,

has the expansion

where  corresponds to
corresponds to  , that is, the singularities of (3.59). Now
, that is, the singularities of (3.59). Now  is a positive Nevanlinna function with graph given in Figure 2.
is a positive Nevanlinna function with graph given in Figure 2.
Clearly, the gradient of  at
at  is positive for all
is positive for all  , that is,
, that is,

If  does not obey (3.50) then the zeros of
does not obey (3.50) then the zeros of

are the poles of  , that is, the
, that is, the  's and
's and  where
where  for
for  . It is evident, from Figure 2, that the number of
. It is evident, from Figure 2, that the number of  's is one more than the number of
's is one more than the number of  's, thus in (3.60),
's, thus in (3.60),  .
.
We now examine the form of  in (3.60). As
in (3.60). As  it follows that
it follows that  , thus
, thus

Hence,  .
.
Using (3.58) we now obtain

Note that  . Let
. Let

then

Now  since if
since if  then
then  , that is,
, that is,  but
but  and
and  so this is not possible. Therefore by Section 2, Nevanlinna result (II), we have that
so this is not possible. Therefore by Section 2, Nevanlinna result (II), we have that

that is, (3.51) holds.
If  does obey (3.50) for
does obey (3.50) for  then
then  . Thus, in Figure 2, one of the
. Thus, in Figure 2, one of the  's,
's,  is equal to
is equal to  and since
and since  is less than the least eigenvalue of the boundary value problem (1.1), (3.50) together with a boundary condition at
is less than the least eigenvalue of the boundary value problem (1.1), (3.50) together with a boundary condition at  (specified later) it follows that
(specified later) it follows that  , as
, as  for all
for all  .
.
Now (3.59) can be written as

and as 

Thus  is a removable singularity. Alternatively, we could substitute in for
is a removable singularity. Alternatively, we could substitute in for  and
and  to illustrate that the singularity at
to illustrate that the singularity at  is removable, see Theorem 3.2. Hence the number of nonremovable
is removable, see Theorem 3.2. Hence the number of nonremovable  's is the same as the number of
's is the same as the number of  's, see Figure 2. So (3.60) becomes
's, see Figure 2. So (3.60) becomes

which may be rewritten as

where  and
and  for
for  .
.
We now examine the form of  in (3.70). As
in (3.70). As  , we have that
, we have that  , thus
, thus

Hence,  . So, from (3.58) with
. So, from (3.58) with  , we obtain
, we obtain

where, as before,

Thus, by Section 2, Nevanlinna result (II), we have that

that is, (3.52) holds.
In Theorem 3.4, we impose a boundary condition at the terminal end point and show how it is transformed according to whether or not  obeys the given boundary condition.
obeys the given boundary condition.
Theorem 3.4.
Consider  obeying the boundary condition at
obeying the boundary condition at  given by
given by

where  is a negative Nevanlinna function, that is,
is a negative Nevanlinna function, that is,  and
and  for
for  . Under the mapping (2.1),
. Under the mapping (2.1),  obeying (3.76) transforms to
obeying (3.76) transforms to  obeying the following.
obeying the following.
(I) If  does not obey (3.76) then
does not obey (3.76) then  obeys
obeys

(II) If  does obey (3.76) then
does obey (3.76) then  obeys
obeys

where  .
.
Proof.
Since  and
and  are defined we do not need to extend the domain of
are defined we do not need to extend the domain of  in order to impose the boundary conditions (3.77) or (3.78).
in order to impose the boundary conditions (3.77) or (3.78).
The mapping (2.1), at  , gives
, gives

From (1.1), with  , we can substitute in for
, we can substitute in for  in the above equation to get
in the above equation to get

Using (3.76), we obtain

But  obeys (1.1) at
obeys (1.1) at  , for
, for  , so that (3.81) becomes
, so that (3.81) becomes

Also, for  , (2.1) together with (3.76) yields
, (2.1) together with (3.76) yields

Therefore,

Let  , then (3.84) may be rewritten as
, then (3.84) may be rewritten as

By Section 2, Nevanlinna result (I), since  is a negative Nevanlinna function it follows that
is a negative Nevanlinna function it follows that  is a positive Nevanlinna function, which has the form
is a positive Nevanlinna function, which has the form

by Section 2, Nevanlinna result (III).
As before  has expansion
has expansion

where  ,
,  , corresponds to the singularities of (3.85), that is, where
, corresponds to the singularities of (3.85), that is, where  . The graph of
. The graph of  is as shown in Figure 3.
is as shown in Figure 3.
As before, the gradient of  at
at  is positive for all
is positive for all  , that is
, that is

If  does not obey (3.76) then the zeros of
does not obey (3.76) then the zeros of

are the poles of  , that is, the
, that is, the  's and
's and  where
where  for
for  . Clearly, from Figure 3, the number of
. Clearly, from Figure 3, the number of  's is the same as the the number of
's is the same as the the number of  's, thus in (3.87),
's, thus in (3.87),  .
.
Next, we examine the form of  in (3.87). As
in (3.87). As  it follows that
it follows that  . Thus
. Thus

Therefore,  . Hence,
. Hence,

where  ,
,  ,
,  and
and  for
for  , which is precisely (3.77).
, which is precisely (3.77).
If  does obey (3.76) for
does obey (3.76) for  then
then  . Thus in Figure 3, one of the
. Thus in Figure 3, one of the  's,
's,  is equal to
is equal to  and since
and since  is less than the least eigenvalue of the boundary value problem (1.1), (3.76) together with a boundary condition at −1 (as given in Theorems 3.2 or 3.3) it follows that
is less than the least eigenvalue of the boundary value problem (1.1), (3.76) together with a boundary condition at −1 (as given in Theorems 3.2 or 3.3) it follows that  , as
, as  for all
for all  .
.
Now

and as 

Thus  is a removable singularity. Again, alternatively, we could have substituted in for
is a removable singularity. Again, alternatively, we could have substituted in for  and
and  to illustrate that the singularity at
to illustrate that the singularity at  is removable, see Theorem 3.2. Hence the number of nonremovable
is removable, see Theorem 3.2. Hence the number of nonremovable  's is one less than the number of
's is one less than the number of  's, see Figure 3.
's, see Figure 3.
So (3.87) becomes

which may be rewritten as

where  and
and  for
for  .
.
Now as  ,
,

So, we obtain

where  ,
,  ,
,  , and
, and  for all
for all  , that is, we obtain (3.78).
, that is, we obtain (3.78).
4. Comparison of the Spectra
In this section, we investigate how the spectrum of the original boundary value problem compares to the spectrum of the transformed boundary value problem. This is done by considering the degree of the eigenparameter polynomial for the various eigenconditions.
Lemma 4.1.
Consider the boundary value problem given by (1.1) for  together with boundary conditions
together with boundary conditions


Then the boundary value problem (1.1), (4.1), (4.2) has  eigenvalues. (Note that the number of unit intervals considered is
eigenvalues. (Note that the number of unit intervals considered is  .)
.)
Proof.
From (1.1), with  , we obtain
, we obtain

Substituting in for  from (4.1) yields
from (4.1) yields

which may be rewritten as

where  ,
,  are real constants.
are real constants.
Now (1.1), for  , together with (4.5) results in
, together with (4.5) results in

where  ,
,  are real constants.
are real constants.
Thus, by induction,

for real constants  ,
,  . Similarly
. Similarly

for real constants  ,
,  .
.
Since  , using boundary condition (4.2) we obtain the following eigencondition:
, using boundary condition (4.2) we obtain the following eigencondition:

where  ,
,  , are real constants.
, are real constants.
Thus, the numerator is a polynomial, in  , of order
, of order  . Note that, none of the roots of this polynomial are given by
. Note that, none of the roots of this polynomial are given by  ,
,  or
or  ,
,  since, from Figures 1 to 3, it is easy to see that none of the eigenvalues of the boundary value problem are equal to the poles of the boundary conditions. Also
since, from Figures 1 to 3, it is easy to see that none of the eigenvalues of the boundary value problem are equal to the poles of the boundary conditions. Also  is not a problem as the curve of the Nevanlinna function never intersects with the horizontal or oblique asymptote. This means that there are no common factors to cancel out. Hence the eigencondition has
is not a problem as the curve of the Nevanlinna function never intersects with the horizontal or oblique asymptote. This means that there are no common factors to cancel out. Hence the eigencondition has  roots giving that the boundary value problem has
roots giving that the boundary value problem has  eigenvalues.
eigenvalues.
As a direct consequence of Theorems 2.1, 3.2, 3.3, 3.4, and Lemma 4.1 we have the following theorem.
Theorem 4.2.
For the original boundary value problem we consider twelve cases, (see Table 1 in the Appendix), each of which has s+l+m+1 eigenvalues. The corresponding transformed boundary value problem for each of the twelve cases, together with the number of eigenvalues for that transformed boundary value problem, is given in Table 1 (see the appendix).
Remark 4.3.
To summarise we have the following.
-
(a)
If
 obeys the boundary conditions at both ends the transformed boundary value problem will have one less eigenvalue than the original boundary value problem, namely,
obeys the boundary conditions at both ends the transformed boundary value problem will have one less eigenvalue than the original boundary value problem, namely,  .
. -
(b)
If
 obeys the boundary condition at one end only the transformed boundary value problem will have the same eigenvalues as the original boundary value problem.
obeys the boundary condition at one end only the transformed boundary value problem will have the same eigenvalues as the original boundary value problem. -
(c)
If
 does not obey any of the boundary conditions the transformed boundary value problem will have one more eigenvalue than the original boundary value problem, namely,
does not obey any of the boundary conditions the transformed boundary value problem will have one more eigenvalue than the original boundary value problem, namely, 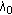 .
.
Corollary 4.4.
If  are the eigenvalues of any one of the original boundary value problems (1)–(9), in Theorem 4.2, with corresponding eigenfunctions
are the eigenvalues of any one of the original boundary value problems (1)–(9), in Theorem 4.2, with corresponding eigenfunctions  then
then
(i) are the eigenvalues of the corresponding transformed boundary value problems (1)–(3), in Theorem 4.2, with corresponding eigenfunctions
are the eigenvalues of the corresponding transformed boundary value problems (1)–(3), in Theorem 4.2, with corresponding eigenfunctions  ;
;
(ii) are the eigenvalues of the corresponding transformed boundary value problems (4)–(9), in Theorem 4.2, with corresponding eigenfunctions
are the eigenvalues of the corresponding transformed boundary value problems (4)–(9), in Theorem 4.2, with corresponding eigenfunctions  .
.
Also, if  are the eigenvalues of any one of the original boundary value problems (10)–(12), in Theorem 4.2, with corresponding eigenfunctions
are the eigenvalues of any one of the original boundary value problems (10)–(12), in Theorem 4.2, with corresponding eigenfunctions  then
then  are the eigenvalues of the corresponding transformed boundary value problems (10)–(12), in Theorem 4.2, with corresponding eigenfunctions
are the eigenvalues of the corresponding transformed boundary value problems (10)–(12), in Theorem 4.2, with corresponding eigenfunctions  .
.
Proof.
By Theorems 2.1, 3.2, 3.3, and 3.4, we have that (2.1) transforms eigenfunctions of the original boundary value problems (1)–(9) to eigenfunctions of the corresponding transformed boundary value problems. In particular, if  are the eigenvalues of one of the original boundary value problems, (1)–(9), with eigenfunctions
are the eigenvalues of one of the original boundary value problems, (1)–(9), with eigenfunctions  then
then
(i) are the eigenfunctions of the corresponding transformed boundary value problem, (1)–(3), with eigenvalues
are the eigenfunctions of the corresponding transformed boundary value problem, (1)–(3), with eigenvalues  . Since the transformed boundary value problems, (1)–(3), have
. Since the transformed boundary value problems, (1)–(3), have  eigenvalues it follows that
eigenvalues it follows that  constitute all the eigenvalues of the transformed boundary value problem;
constitute all the eigenvalues of the transformed boundary value problem;
(ii) are the eigenfunctions of the corresponding transformed boundary value problem, (4)–(9), with eigenvalues
are the eigenfunctions of the corresponding transformed boundary value problem, (4)–(9), with eigenvalues  . Since the transformed boundary value problems, (4)–(9), have
. Since the transformed boundary value problems, (4)–(9), have  eigenvalues it follows that
eigenvalues it follows that  constitute all the eigenvalues of the transformed boundary value problem.
constitute all the eigenvalues of the transformed boundary value problem.
Also, again by Theorems 2.1, 3.2, 3.3, and 3.4, we have that (2.1) transforms eigenfunctions of the original boundary value problems (10)–(12) to eigenfunctions of the corresponding transformed boundary value problems. In particular, if  are the eigenvalues of one of the original boundary value problems, (10)–(12), with eigenfunctions
are the eigenvalues of one of the original boundary value problems, (10)–(12), with eigenfunctions  then
then  are the eigenfunctions of the corresponding transformed boundary value problem, (10)–(12), with eigenvalues
are the eigenfunctions of the corresponding transformed boundary value problem, (10)–(12), with eigenvalues  . Since the transformed boundary value problems, (10)–(12), have
. Since the transformed boundary value problems, (10)–(12), have  eigenvalues it follows that
eigenvalues it follows that  constitute all the eigenvalues of the transformed boundary value problem.
constitute all the eigenvalues of the transformed boundary value problem.
References
Binding PA, Browne PJ, Watson BA: Spectral isomorphisms between generalized Sturm-Liouville problems. In Linear Operators and Matrices, Operator Theory: Advances and Applications. Volume 130. Birkhäuser, Basel, Switzerland; 2002:135-152.
Browne PJ, Nillsen RV: On difference operators and their factorization. Canadian Journal of Mathematics 1983, 35(5):873-897. 10.4153/CJM-1983-050-2
Binding PA, Browne PJ, Watson BA: Sturm-Liouville problems with boundary conditions rationally dependent on the eigenparameter. II. Journal of Computational and Applied Mathematics 2002, 148(1):147-168. 10.1016/S0377-0427(02)00579-4
Binding PA, Browne PJ, Watson BA: Sturm-Liouville problems with reducible boundary conditions. Proceedings of the Edinburgh Mathematical Society. Series II 2006, 49(3):593-608. 10.1017/S0013091505000131
Binding PA, Browne PJ, Watson BA: Transformations between Sturm-Liouville problems with eigenvalue dependent and independent boundary conditions. Bulletin of the London Mathematical Society 2001, 33(6):749-757. 10.1112/S0024609301008177
Ding H-Y, Sun Y-P, Xue F-C: A hierarchy of differential-difference equations, conservation laws and new integrable coupling system. Communications in Nonlinear Science and Numerical Simulation 2010, 15(8):2037-2043. 10.1016/j.cnsns.2009.08.022
Luo L, Fan E-G: A hierarchy of differential-difference equations and their integrable couplings. Chinese Physics Letters 2007, 24(6):1444-1447. 10.1088/0256-307X/24/6/005
Clarkson PA, Hone ANW, Joshi N: Hierarchies of difference equations and Bäcklund transformations. Journal of Nonlinear Mathematical Physics 2003, 10(supplement 2):13-26. 10.2991/jnmp.2003.10.s2.2
Wu Y, Geng X: A new hierarchy of integrable differential-difference equations and Darboux transformation. Journal of Physics A 1998, 31(38):L677-L684. 10.1088/0305-4470/31/38/004
Currie S, Love AD: Transformations of difference equations I. Advances in Difference Equations 2010, 2010:-22.
Currie S, Love AD: Transformations of difference equations II. Advances in Difference Equations 2010, 2010:-23.
Binding PA, Browne PJ, Watson BA: Sturm-Liouville problems with boundary conditions rationally dependent on the eigenparameter. I. Proceedings of the Edinburgh Mathematical Society. Series II 2002, 45(3):631-645.
Gautschi W: Orthogonal Polynomials: Computation and Approximation, Numerical Mathematics and Scientific Computation. Oxford University Press, New York, NY, USA; 2004:x+301.
Miller KS: Linear Difference Equations. W. A. Benjamin, New York, NY, USA; 1968:x+105.
Miller KS: An Introduction to the Calculus of Finite Differences and Difference Equations. Dover, New York, NY, USA; 1966:viii+167.
Atkinson FV: Discrete and Continuous Boundary Problems, Mathematics in Science and Engineering. Volume 8. Academic Press, New York, NY, USA; 1964:xiv+570.
Teschl G: Jacobi Operators and Completely Integrable Nonlinear Lattices, Mathematical Surveys and Monographs. Volume 72. American Mathematical Society, Providence, RI, USA; 2000:xvii+351.
Acknowledgments
The authors would like to thank Professor Bruce A. Watson for his useful input. S. Currie is supported by NRF Grant nos. TTK2007040500005 and FA2007041200006.
Author information
Authors and Affiliations
Corresponding author
Additional information
An erratum to this article is available at http://dx.doi.org/10.1186/1687-2770-2012-66.
Twelve Cases for Theorem 4.2
See Table 1.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Currie, S., Love, A. Hierarchies of Difference Boundary Value Problems. Bound Value Probl 2011, 743135 (2011). https://doi.org/10.1155/2011/743135
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/743135

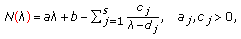
 -Dependent Boundary Conditions
-Dependent Boundary Conditions
 .
.

 .
.

 .
.
 obeys the boundary conditions at both ends the transformed boundary value problem will have one less eigenvalue than the original boundary value problem, namely,
obeys the boundary conditions at both ends the transformed boundary value problem will have one less eigenvalue than the original boundary value problem, namely,  .
. obeys the boundary condition at one end only the transformed boundary value problem will have the same eigenvalues as the original boundary value problem.
obeys the boundary condition at one end only the transformed boundary value problem will have the same eigenvalues as the original boundary value problem. does not obey any of the boundary conditions the transformed boundary value problem will have one more eigenvalue than the original boundary value problem, namely,
does not obey any of the boundary conditions the transformed boundary value problem will have one more eigenvalue than the original boundary value problem, namely, 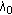 .
.