- Research Article
- Open access
- Published:
Lagrangian Stability of a Class of Second-Order Periodic Systems
Boundary Value Problems volume 2011, Article number: 845413 (2011)
Abstract
We study the following second-order differential equation:  , where
, where  (
( ),
),  and
and  are positive constants, and
are positive constants, and  satisfies
satisfies  . Under some assumptions on the parities of
. Under some assumptions on the parities of  and
and  , by a small twist theorem of reversible mapping we obtain the existence of quasiperiodic solutions and boundedness of all the solutions.
, by a small twist theorem of reversible mapping we obtain the existence of quasiperiodic solutions and boundedness of all the solutions.
1. Introduction and Main Result
In the early 1960s, Littlewood [1] asked whether or not the solutions of the Duffing-type equation

are bounded for all time, that is, whether there are resonances that might cause the amplitude of the oscillations to increase without bound.
The first positive result of boundedness of solutions in the superlinear case (i.e.,  as
as  ) was due to Morris [2]. By means of KAM theorem, Morris proved that every solution of the differential equation (1.1) is bounded if
) was due to Morris [2]. By means of KAM theorem, Morris proved that every solution of the differential equation (1.1) is bounded if  , where
, where  is piecewise continuous and periodic. This result relies on the fact that the nonlinearity
is piecewise continuous and periodic. This result relies on the fact that the nonlinearity  can guarantee the twist condition of KAM theorem. Later, several authors (see [3–5]) improved Morris's result and obtained similar result for a large class of superlinear function
can guarantee the twist condition of KAM theorem. Later, several authors (see [3–5]) improved Morris's result and obtained similar result for a large class of superlinear function  .
.
When  satisfies
satisfies

that is, the differential equation (1.1) issemilinear, similar results also hold, but the proof is more difficult since there may be resonant case. We refer to [6–8] and the references therein.
In [8] Liu considered the following equation:

where  as
as  and
and  is a
is a  -periodic function. After introducing new variables, the differential equation (1.3) can be changed into a Hamiltonian system. Under some suitable assumptions on
-periodic function. After introducing new variables, the differential equation (1.3) can be changed into a Hamiltonian system. Under some suitable assumptions on  and
and  , by using a variant of Moser's small twist theorem [9] to the Pioncaré map, the author obtained the existence of quasi-periodic solutions and the boundedness of all solutions.
, by using a variant of Moser's small twist theorem [9] to the Pioncaré map, the author obtained the existence of quasi-periodic solutions and the boundedness of all solutions.
Then the result is generalized to a class of  -Laplacian differential equation.Yang [10] considered the following nonlinear differential equation
-Laplacian differential equation.Yang [10] considered the following nonlinear differential equation

where  is bounded,
is bounded,  is periodic. The idea is also to change the original problem to Hamiltonian system and then use a twist theorem of area-preserving mapping to the Pioncaré map.
is periodic. The idea is also to change the original problem to Hamiltonian system and then use a twist theorem of area-preserving mapping to the Pioncaré map.
The above differential equation essentially possess Hamiltonian structure. It is well known that the Hamiltonian structure and reversible structure have many similar property. Especially, they have similar KAM theorem.
Recently, Liu [6] studied the following equation:

where  is a positive constant and
is a positive constant and  is
is  -periodic in
-periodic in  . Under some assumption of
. Under some assumption of  and
and  , the differential equation (1.5) has a reversible structure. Suppose that
, the differential equation (1.5) has a reversible structure. Suppose that  satisfies
satisfies

where  and
and  . Moreover,
. Moreover,

where  is a constant. Note that here and below we always use
is a constant. Note that here and below we always use  to indicate some constants. Assume that there exists
to indicate some constants. Assume that there exists  such that
such that

Then, the following conclusions hold true.
(i)There exist  and a closed set
and a closed set  having positive measure such that for any
having positive measure such that for any  , there exists a quasi-periodic solution for (1.5) with the basic frequency
, there exists a quasi-periodic solution for (1.5) with the basic frequency  .
.
(ii)Every solution of (1.5) is bounded.
Motivated by the papers [6, 8, 10], we consider the following  -Laplacian equation:
-Laplacian equation:

where 
 ,
,  , and
, and  are constants. We want to generalize the result in [6] to a class of
are constants. We want to generalize the result in [6] to a class of  -Laplacian-type differential equations of the form (1.9). The main idea is similar to that in [6]. We will assume that the functions
-Laplacian-type differential equations of the form (1.9). The main idea is similar to that in [6]. We will assume that the functions  and
and  have some parities such that the differential system (1.9) still has a reversible structure. After some transformations, we change the systems (1.9) to a form of small perturbation of integrable reversible system. Then a KAM Theorem for reversible mapping can be applied to the Poincaré mapping of this nearly integrable reversible system and some desired result can be obtained.
have some parities such that the differential system (1.9) still has a reversible structure. After some transformations, we change the systems (1.9) to a form of small perturbation of integrable reversible system. Then a KAM Theorem for reversible mapping can be applied to the Poincaré mapping of this nearly integrable reversible system and some desired result can be obtained.
Our main result is the following theorem.
Theorem 1.1.
Suppose that  and
and  are of class
are of class  in their arguments and
in their arguments and  -periodic with respect to t such that
-periodic with respect to t such that

Moreover, suppose that there exists  such that
such that

for all  , for all
, for all  ,
,  . Then every solution of (1.9) is bounded.
. Then every solution of (1.9) is bounded.
Remark 1.2.
Our main nonlinearity  in (1.9) corresponds to
in (1.9) corresponds to  in (1.5). Although it is more special than
in (1.5). Although it is more special than  , it makes no essential difference of proof and can simplify our proof greatly. It is easy to see from the proof that this main nonlinearity is used to guarantee the small twist condition.
, it makes no essential difference of proof and can simplify our proof greatly. It is easy to see from the proof that this main nonlinearity is used to guarantee the small twist condition.
2. The Proof of Theorem
The proof of Theorem 1.1 is based on Moser's small twist theorem for reversible mapping. It mainly consists of two steps. The first one is to find an equivalent system, which has a nearly integrable form of a reversible system. The second one is to show that Pincaré map of the equivalent system satisfies some twist theorem for reversible mapping.
2.1. Action-Angle Variables
We first recall the definitions of reversible system. Let 

 be an open domain, and
be an open domain, and  be continuous. Suppose
be continuous. Suppose  is an involution (i.e.,
is an involution (i.e.,  is a
is a  -diffeomorphism such that
-diffeomorphism such that  ) satisfying
) satisfying  . The differential equations system
. The differential equations system

is called reversible with respect to  , if
, if

with  denoting the Jacobian matrix of
denoting the Jacobian matrix of  .
.
We are interested in the special involution  with
with  . Let
. Let  . Then
. Then  is reversible with respect to
is reversible with respect to  if and only if
if and only if

Below we will see that the symmetric properties (1.10) imply a reversible structure of the system (1.9).
Let  . Then
. Then  , where
, where  satisfies
satisfies  . Hence, the differential equation (1.9) is changed into the following planar system:
. Hence, the differential equation (1.9) is changed into the following planar system:

By (1.10) it is easy to see that the system (2.4) is reversible with respect to the involution  .
.
Below we will write the reversible system (2.4) as a form of small perturbation. For this purpose we first introduce action-angle variables  .
.
Consider the homogeneous differential equation:

This equation takes as an integrable part of (1.9). We will use its solutions to construct a pair of action-angle variables. One of solutions for (2.5) is the function  as defined below. Let the number
as defined below. Let the number  defined by
defined by

We define the function  , implicitly by
, implicitly by

The function  will be extended to the whole real axis
will be extended to the whole real axis  as explained below, and the extension will be denoted by
as explained below, and the extension will be denoted by  . Define
. Define  on
on  by
by  . Then, we define
. Then, we define  on
on  such that
such that  is an odd function. Finally, we extend
is an odd function. Finally, we extend  to
to  by
by  -periodicity. It is not difficult to verify that
-periodicity. It is not difficult to verify that  has the following properties:
has the following properties:
(i) ,
,  ;
;
(ii) ;
;
(iii) is an odd periodic function with period
is an odd periodic function with period  .
.
It is easy to verify that  satisfies
satisfies

with initial condition  . Define a transformation
. Define a transformation  by
by

It is easy to see that

Since the Jacobian matrix of  is nonsingular for
is nonsingular for  , the transformation
, the transformation  is a local homeomorphism at each point
is a local homeomorphism at each point  of the set
of the set  , while
, while  is a global homeomorphism from
is a global homeomorphism from  to
to  . Under the transformation
. Under the transformation  the system (2.4) is changed to
the system (2.4) is changed to

where

with  .
.
It is easily verified that  and
and  and so the system (2.11) is reversible with respect to the involution
and so the system (2.11) is reversible with respect to the involution  .
.
2.2. Some Lemmas
To estimate  and
and  , we need some definitions and lemmas.
, we need some definitions and lemmas.
Lemma 2.1.
Let  . If
. If  and
and  satisfy (1.11), then
satisfy (1.11), then

for  ,
,  .
.
Proof.
We only prove the second inequality since the first one can be proved similarly.

To describe the estimates in Lemma 2.1, we introduce function space  , where
, where  is a function of
is a function of  .
.
Definition 2.2.
Let  . We say
. We say  , if for
, if for  , there exist
, there exist  and
and  such that
such that

Lemma 2.3 (see [6]).
The following conclusions hold true:
(i)if  , then
, then  and
and  ;
;
(ii)if  and
and  , then
, then  ;
;
(iii)Suppose  satisfy that, there exists
satisfy that, there exists  such that for
such that for  ,
,

If  ,
,  ,
,  , then, we have
, then, we have

Moreover,

Proof.
This lemma was proved in [6], but we give the proof here for reader's convenience. Since (i) and (ii) are easily verified by definition, so we only prove (iii). Let

Since  , we have
, we have  . So
. So  . Thus
. Thus  is bounded and so
is bounded and so  . Similarly, we have
. Similarly, we have

For  , we have
, we have

Since  , it follows that
, it follows that

Let  . Since
. Since  , we know that for
, we know that for  sufficiently large
sufficiently large

By the property of  , we have
, we have

for  sufficiently large.
sufficiently large.
If  , then by a direct computation, we have
, then by a direct computation, we have

where the sum is found for the indices satisfying

Without loss of generality, we assume that

Furthermore, we suppose that among  , there are
, there are  numbers which equal to 0, and among
numbers which equal to 0, and among  , there are
, there are  numbers which equal to 0.
numbers which equal to 0.
Since

we have

and then,

Obviously

Since

By the condition of (iii) we obtain

In the same way we can consider  and we omit the details.
and we omit the details.
2.3. Some Estimates
The following lemma gives the estimate for  and
and  .
.
Lemma 2.4.
 ,
,  , where
, where  .
.
Proof.
Since  , we first consider
, we first consider  and
and  . By Lemma 2.1,
. By Lemma 2.1,  . Again
. Again  , using the conclusion (iii) of Lemma 2.3, we have
, using the conclusion (iii) of Lemma 2.3, we have  , where
, where  . Note that
. Note that  and
and  , we have
, we have  . In the same way we can prove
. In the same way we can prove  . Thus Lemma 2.4 is proved.
. Thus Lemma 2.4 is proved.
Since  , we get
, we get  . So
. So  for sufficiently large
for sufficiently large  . When
. When  the system (2.11) is equivalent to the following system:
the system (2.11) is equivalent to the following system:

It is easy to see that  and
and  . Hence, system (2.34) is reversible with respect to the involution
. Hence, system (2.34) is reversible with respect to the involution  .
.
We will prove that the Poincaré mapping can be a small perturbation of integrable reversible mapping. For this purpose, we write (2.34) as a small perturbation of an integrable reversible system. Write the system (2.34) in the form

where  ,
,  , with
, with  and
and  defined in (2.11). It follows
defined in (2.11). It follows  , and so (2.35) is also reversible with respect to the involution
, and so (2.35) is also reversible with respect to the involution  . Below we prove that
. Below we prove that  and
and  are smaller perturbations.
are smaller perturbations.
Lemma 2.5.
 ,
,  .
.
Proof.
If  is sufficiently large, then
is sufficiently large, then  and so
and so  . Hence
. Hence

It is easy to verify that

where  ,
,  , and
, and  and
and  are defined in the same way as
are defined in the same way as  and
and  .
.
So, we have

where

So

Thus,  . In the same way, we have
. In the same way, we have  .
.
Now we change system (2.35) to

where  and
and  . By the proof of Lemma 2.4, we know
. By the proof of Lemma 2.4, we know  and
and  . Thus,
. Thus,  and
and  where
where

with  ,
,  .
.
2.4. Coordination Transformation
Lemma 2.6.
There exists a transformation of the form

such that the system (2.41) is changed into the form

where  satisfy:
satisfy:

Moreover, the system (2.44) is reversible with respect to the involution G:  .
.
Proof.
Let

then

It is easy to see that

Hence the map  with
with  is diffeomorphism for
is diffeomorphism for  . Thus, there is a function
. Thus, there is a function  such that
such that

where

Under this transformation, the system (2.41) is changed to (2.44) with

Below we estimate  and
and  . We only consider
. We only consider  since
since  can be considered similarly or even simpler.
can be considered similarly or even simpler.
Obviously,

Note that

By the third conclusion of Lemma 2.3, we have that

In the same way as the above, we have

and so

By (2.54) and (2.56), noting that  , it follows that
, it follows that

Since  , the system (2.44) is reversible in
, the system (2.44) is reversible in  with respect to the involution
with respect to the involution  . Thus Lemma 2.6 is proved.
. Thus Lemma 2.6 is proved.
Now we make average on the nonlinear term  in the second equation of (2.44).
in the second equation of (2.44).
Lemma 2.7.
There exists a transformation of the form

which changes (2.44) to the form

where  with
with  and the new perturbations
and the new perturbations  satisfy:
satisfy:

Moreover, the system (2.59) is reversible with respect to the involution G:  .
.
Proof.
We choose

Then

Defined a transformation by

Then the system of (2.44) becomes

where

It is easy to very that

which implies that the system (2.59) is reversible with respect to the involution G:  . In the same way as the proof of
. In the same way as the proof of  and
and  , we have
, we have

Thus Lemma 2.7 is proved.
Below we introduce a small parameter such that the system (2.4) is written as a form of small perturbation of an integrable.
Let

Since

then

Now, we define a transformation by

Then the system (2.59) has the form

where

Lemma 2.8.
The perturbations  and
and  satisfy the following estimates:
satisfy the following estimates:

Proof.
By (2.73), (2.60) and noting that  , it follows that
, it follows that

In the same way,  . The estimates (2.74) for
. The estimates (2.74) for  follow easily from (2.60).
follow easily from (2.60).
2.5. Poincaré Map and Twist Theorems for Reversible Mapping
We can use a small twist theorem for reversible mapping to prove that the Pioncaré map  has an invariant closed curve, if
has an invariant closed curve, if  is sufficiently small. The earlier result was due to Moser [11, 12], and Sevryuk [13]. Later, Liu [14] improved the previous results. Let us first recall the theorem in [14].
is sufficiently small. The earlier result was due to Moser [11, 12], and Sevryuk [13]. Later, Liu [14] improved the previous results. Let us first recall the theorem in [14].
Let  be a finite part of cylinder
be a finite part of cylinder  , where
, where  , we denote by
, we denote by  the class of Jordan curves in
the class of Jordan curves in  that are homotopic to the circle
that are homotopic to the circle  . The subclass of
. The subclass of  composed of those curves lying in
composed of those curves lying in  will be denoted by
will be denoted by  , that is,
, that is,

Consider a mapping  , which is reversible with respect to
, which is reversible with respect to  . Moreover, a lift of
. Moreover, a lift of  can be expressed in the form:
can be expressed in the form:

where  is a real number,
is a real number,  is a small parameter, the functions
is a small parameter, the functions  ,
,  ,
,  , and
, and  are
are  periodic.
periodic.
Lemma 2.9 (see [14, Theorem 2]).
Let  with an integer n and the functions
with an integer n and the functions  ,
,  ,
,  , and
, and  satisfy
satisfy

In addition, we assume that there is a function  satisfying
satisfying

Moreover, suppose that there are two numbers  , and
, and  such that
such that  and
and

where

Then there exist  and
and  such that, if
such that, if  and
and

the mapping  has an invariant curve in
has an invariant curve in  , the constant
, the constant  and
and  depend on
depend on  , and
, and  . In particular,
. In particular,  is independent of
is independent of  .
.
Remark 2.10.
If  satisfy all the conditions of Lemma 2.9, then Lemma 2.9 still holds.
satisfy all the conditions of Lemma 2.9, then Lemma 2.9 still holds.
Lemma 2.11 (see [14, Theorem 1]).
Assume that  and
and  ,
, 
 and
and  . If
. If

then there exist  and
and  such that
such that  has an invariant curve in
has an invariant curve in  if
if  and
and

The constants  and
and  depend on
depend on  only.
only.
We use Lemmas 2.9 and 2.11 to prove our Theorem 1.1. For the reversible mapping (2.86),  ,
,  .
.
2.6. Invariant Curves
From (2.73) and (2.66), we have

which yields that system (2.72) is reversible in  with respect to the involution
with respect to the involution  . Denote by
. Denote by  the Poincare map of (2.72), then
the Poincare map of (2.72), then  is also reversible with the same involution
is also reversible with the same involution  and has the form
and has the form

where  and
and  . Moreover,
. Moreover,  and
and  satisfy
satisfy

Case 1 ( is rational).
is rational).
Let  , it is easy to see that
, it is easy to see that

Since  only depends on
only depends on  , and
, and  , all conditions in Lemma 2.9 hold.
, all conditions in Lemma 2.9 hold.
Case 2 ( is irrational).
is irrational).
Since

all the assumptions in Lemma 2.11 hold.
Thus, in the both cases, the Poincare mapping  always have invariant curves for
always have invariant curves for  being sufficient small. Since
being sufficient small. Since  , we know that for any
, we know that for any  , there is an invariant curve of the Poincare mapping, which guarantees the boundedness of solutions of the system (2.11). Hence, all the solutions of (1.9) are bounded.
, there is an invariant curve of the Poincare mapping, which guarantees the boundedness of solutions of the system (2.11). Hence, all the solutions of (1.9) are bounded.
References
Littlewood J: Unbounded solutions of
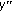 +
+  (
(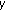 ) =
) = 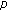 (
(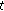 ). Journal of the London Mathematical Society 1996, 41: 133–149.
). Journal of the London Mathematical Society 1996, 41: 133–149.Morris GR: A case of boundedness in Littlewood's problem on oscillatory differential equations. Bulletin of the Australian Mathematical Society 1976, 14(1):71–93. 10.1017/S0004972700024862
Liu B: Boundedness for solutions of nonlinear Hill's equations with periodic forcing terms via Moser's twist theorem. Journal of Differential Equations 1989, 79(2):304–315. 10.1016/0022-0396(89)90105-8
Levi M: Quasiperiodic motions in superquadratic time-periodic potentials. Communications in Mathematical Physics 1991, 143(1):43–83. 10.1007/BF02100285
Dieckerhoff R, Zehnder E: Boundedness of solutions via the twist-theorem. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze 1987, 14(1):79–95.
Liu B: Quasiperiodic solutions of semilinear Liénard equations. Discrete and Continuous Dynamical Systems 2005, 12(1):137–160.
Küpper T, You J: Existence of quasiperiodic solutions and Littlewood's boundedness problem of Duffing equations with subquadratic potentials. Nonlinear Analysis. Theory, Methods & Applications 1999, 35: 549–559. 10.1016/S0362-546X(97)00709-8
Liu B: Boundedness of solutions for semilinear Duffing equations. Journal of Differential Equations 1998, 145(1):119–144. 10.1006/jdeq.1997.3406
Moser J: On invariant curves of area-preserving mappings of an annulus. Nachrichten der Akademie der Wissenschaften in Göttingen. II. Mathematisch-Physikalische Klasse 1962, 1962: 1–20.
Yang X: Boundedness of solutions for nonlinear oscillations. Applied Mathematics and Computation 2003, 144(2–3):187–198. 10.1016/S0096-3003(02)00399-5
Moser J: Convergent series expansions for quasi-periodic motions. Mathematische Annalen 1967, 169: 136–176. 10.1007/BF01399536
Moser J: Stable and Random Motions in Dynamical Systems. Princeton University Press, Princeton, NJ, USA; 1973:viii+198.
Sevryuk MB: Reversible Systems, Lecture Notes in Mathematics. Volume 1211. Springer, Berlin, Germany; 1986:vi+319.
Liu B, Song JJ: Invariant curves of reversible mappings with small twist. Acta Mathematica Sinica 2004, 20(1):15–24. 10.1007/s10114-004-0316-4
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jiang, S., Xu, J. & Zhang, F. Lagrangian Stability of a Class of Second-Order Periodic Systems. Bound Value Probl 2011, 845413 (2011). https://doi.org/10.1155/2011/845413
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/845413
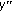 +
+  (
(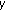 ) =
) = 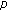 (
(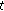 ). Journal of the London Mathematical Society 1996, 41: 133–149.
). Journal of the London Mathematical Society 1996, 41: 133–149.