- Research Article
- Open access
- Published:
Multiple Positive Solutions for Second-Order  -Laplacian Dynamic Equations with Integral Boundary Conditions
-Laplacian Dynamic Equations with Integral Boundary Conditions
Boundary Value Problems volume 2011, Article number: 867615 (2011)
Abstract
We are concerned with the following second-order  -Laplacian dynamic equations on time scales
-Laplacian dynamic equations on time scales  ,
,  , with integral boundary conditions
, with integral boundary conditions  ,
,  . By using Legget-Williams fixed point theorem, some criteria for the existence of at least three positive solutions are established. An example is presented to illustrate the main result.
. By using Legget-Williams fixed point theorem, some criteria for the existence of at least three positive solutions are established. An example is presented to illustrate the main result.
1. Introduction
Boundary value problems with  -Laplacian have received a lot of attention in recent years. They often occur in the study of the
-Laplacian have received a lot of attention in recent years. They often occur in the study of the  -dimensional
-dimensional  -Laplacian equation, non-Newtonian fluid theory, and the turbulent flow of gas in porous medium [1–7]. Many works have been carried out to discuss the existence of solutions or positive solutions and multiple solutions for the local or nonlocal boundary value problems.
-Laplacian equation, non-Newtonian fluid theory, and the turbulent flow of gas in porous medium [1–7]. Many works have been carried out to discuss the existence of solutions or positive solutions and multiple solutions for the local or nonlocal boundary value problems.
On the other hand, the study of dynamic equations on time scales goes back to its founder Stefan Hilger [8] and is a new area of still fairly theoretical exploration in mathematics. Motivating the subject is the notion that dynamic equations on time scales can build bridges between continuous and discrete equations. Further, the study of time scales has led to several important applications, for example, in the study of insect population models, neural networks, heat transfer, and epidemic models, we refer to [8–10]. In addition, the study of BVPs on time scales has received a lot of attention in the literature, with the pioneering existence results to be found in [11–16].
However, existence results are not available for dynamic equations on time scales with integral boundary conditions. Motivated by above, we aim at studying the second-order  -Laplacian dynamic equations on time scales in the form of
-Laplacian dynamic equations on time scales in the form of

with integral boundary condition

where  is positive parameter,
is positive parameter,  for
for  with
with  and
and  ,
,  is the delta derivative,
is the delta derivative,  is the nabla derivative,
is the nabla derivative,  is a time scale which is a nonempty closed subset of
is a time scale which is a nonempty closed subset of  with the topology and ordering inherited from
with the topology and ordering inherited from  , 0 and
, 0 and  are points in
are points in  , an interval
, an interval  ,
,  with
with  for all
for all  ,
,  ,
,  with
with  , and where
, and where  .
.
The main purpose of this paper is to establish some sufficient conditions for the existence of at least three positive solutions for BVPs (1.1)-(1.2) by using Legget-Williams fixed point theorem. This paper is organized as follows. In Section 2, some useful lemmas are established. In Section 3, by using Legget-Williams fixed point theorem, we establish sufficient conditions for the existence of at least three positive solutions for BVPs (1.1)-(1.2). An illustrative example is given in Section 4.
2. Preliminaries
In this section, we will first recall some basic definitions and lemmas which are used in what follows.
Definition 2.1 (see [8]).
A time scale  is an arbitrary nonempty closed subset of the real set
is an arbitrary nonempty closed subset of the real set  with the topology and ordering inherited from
with the topology and ordering inherited from  . The forward and backward jump operators
. The forward and backward jump operators  and the graininess
and the graininess  are defined, respectively, by
are defined, respectively, by

The point  is called left-dense, left-scattered, right-dense, or right-scattered if
is called left-dense, left-scattered, right-dense, or right-scattered if  ,
,  , and
, and  or
or  , respectively. Points that are right-dense and left-dense at the same time are called dense. If
, respectively. Points that are right-dense and left-dense at the same time are called dense. If  has a left-scattered maximum
has a left-scattered maximum  , defined
, defined  ; otherwise, set
; otherwise, set  . If
. If  has a right-scattered minimum
has a right-scattered minimum  , defined
, defined  ; otherwise, set
; otherwise, set  .
.
Definition 2.2 (see [8]).
For  and
and  , then the delta derivative of
, then the delta derivative of  at the point
at the point  is defined to be the number
is defined to be the number  (provided it exists) with the property that for each
(provided it exists) with the property that for each  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

For  and
and  , then the nabla derivative of
, then the nabla derivative of  at the point
at the point  is defined to be the number
is defined to be the number  (provided it exists) with the property that for each
(provided it exists) with the property that for each  , there is a neighborhood
, there is a neighborhood  of
of  such that
such that

Definition 2.3 (see [8]).
A function  is rd-continuous provided it is continuous at each right-dense point in
is rd-continuous provided it is continuous at each right-dense point in  and has a left-sided limit at each left-dense point in
and has a left-sided limit at each left-dense point in  . The set of rd-continuous functions
. The set of rd-continuous functions  will be denoted by
will be denoted by  . A function
. A function  is left-dense continuous (i.e., ld-continuous) if
is left-dense continuous (i.e., ld-continuous) if  is continuous at each left-dense point in
is continuous at each left-dense point in  and its right-sided limit exists (finite) at each right-dense point in
and its right-sided limit exists (finite) at each right-dense point in  . The set of left-dense continuous functions
. The set of left-dense continuous functions  will be denoted by
will be denoted by  .
.
Definition 2.4 (see [8]).
If  , then we define the delta integral by
, then we define the delta integral by

If  , then we define the nabla integral by
, then we define the nabla integral by

Lemma 2.5 (see [8]).
If  and
and  , then
, then

If  and
and  , then
, then

Let the Banach space

be endowed with the norm  , where
, where

and choose a cone  defined by
defined by

Lemma 2.6.
If  , then
, then  for all
for all  .
.
Proof.
If  , then
, then  . It follows that
. It follows that

With  and
and  , one obtains
, one obtains

Therefore,

From (2.11)–(2.13), we can get that

So Lemma 2.6 is proved.
Lemma 2.7.
 is a solution of BVPs (1.1)-(1.2) if and only if
is a solution of BVPs (1.1)-(1.2) if and only if  is a solution of the following integral equation:
is a solution of the following integral equation:

where

Proof.
First assume  is a solution of BVPs (1.1)-(1.2); then we have
is a solution of BVPs (1.1)-(1.2); then we have

That is,

Integrating (2.18) from  to
to  , it follows that
, it follows that

Together with (2.19) and  , we obtain
, we obtain

Thus,

namely,

Substituting (2.22) into (2.19), we obtain

The proof of sufficiency is complete.
Conversely, assume  is a solution of the following integral equation:
is a solution of the following integral equation:

It follows that

So  . Furthermore, we have
. Furthermore, we have

which imply that

The proof of Lemma 2.7 is complete.
Define the operator  by
by

for all  . Obviously,
. Obviously,  for all
for all  .
.
Lemma 2.8.
If  , then
, then  .
.
Proof.
It is easily obtained from the second part of the proof in Lemma 2.7. The proof is complete.
Lemma 2.9.
 is complete continuous.
is complete continuous.
Proof.
First, we show that  maps bounded set into itself. Assume
maps bounded set into itself. Assume  is a positive constant and
is a positive constant and  . Note that the continuity of
. Note that the continuity of  guarantees that there is a
guarantees that there is a  such that
such that  for all
for all  . So we get from
. So we get from  and
and  that
that


That is,  is uniformly bounded. In addition, notice that
is uniformly bounded. In addition, notice that

which implies that

which implies that

That is,

So  is equicontinuous for any
is equicontinuous for any  . Using Arzela-Ascoli theorem on time scales [17], we obtain that
. Using Arzela-Ascoli theorem on time scales [17], we obtain that  is relatively compact. In view of Lebesgue's dominated convergence theorem on time scales [18], it is easy to prove that
is relatively compact. In view of Lebesgue's dominated convergence theorem on time scales [18], it is easy to prove that  is continuous. Hence,
is continuous. Hence,  is complete continuous. The proof of this lemma is complete.
is complete continuous. The proof of this lemma is complete.
Let  and
and  be nonnegative continuous convex functionals on a pone
be nonnegative continuous convex functionals on a pone  ,
,  a nonnegative continuous concave functional on
a nonnegative continuous concave functional on  , and
, and  positive numbers with
positive numbers with  we defined the following convex sets:
we defined the following convex sets:

and introduce two assumptions with regard to the functionals  ,
,  as follows:
as follows:
(H1) there exists  such that
such that  for all
for all  ;
;
(H2) for any
for any  and
and  .
.
The following fixed point theorem duo to Bai and Ge is crucial in the arguments of our main result.
Lemma 2.10 (see [19]).
Let  be Banach space,
be Banach space,  a cone, and
a cone, and  ,
,  . Assume that
. Assume that  and
and  are nonnegative continuous convex functionals satisfying (H1) and (H2),
are nonnegative continuous convex functionals satisfying (H1) and (H2),  is a nonnegative continuous concave functional on
is a nonnegative continuous concave functional on  such that
such that  for all
for all  , and
, and  is a complete continuous operator. Suppose
is a complete continuous operator. Suppose
(C1) ,
,  for
for  ;
;
(C2) ,
,  for
for  ;
;
(C3) for
for  with
with  .
.
Then  has at least three fixed points
has at least three fixed points  with
with

3. Main Result
In this section, we will give sufficient conditions for the existence of at least three positive solutions to BVPs (1.1)-(1.2).
Theorem 3.1.
Suppose that there are positive numbers  ,
,  , and
, and  with
with  ,
,  and
and  such that the following conditions are satisfied.
such that the following conditions are satisfied.
(H3) for all
for all  , where
, where

(H4) for all
for all  .
.
(H5) for all
for all  , where
, where

Then BVPs (1.1)-(1.2) have at least three positive solutions.
Proof.
By the definition of the operator  and its properties, it suffices to show that the conditions of Lemma 2.10 hold with respect to the operator
and its properties, it suffices to show that the conditions of Lemma 2.10 hold with respect to the operator  .
.
Let the nonnegative continuous convex functionals  ,
,  and the nonnegative continuous concave functional
and the nonnegative continuous concave functional  be defined on the cone
be defined on the cone  by
by

Then it is easy to see that  and (H1)-(H2) hold.
and (H1)-(H2) hold.
First of all, we show that  . In fact, if
. In fact, if  , then
, then

and assumption (H3) implies that

On the other hand, for  , there is
, there is  ; thus
; thus

Therefore,  .
.
In the same way, if  , then assumption (H4) implies
, then assumption (H4) implies

As in the argument above, we can get that  . Thus, condition (C2) of Lemma 2.10 holds.
. Thus, condition (C2) of Lemma 2.10 holds.
To check condition (C1) in Lemma 2.10. Let  . We choose
. We choose  for
for  . It is easy to see that
. It is easy to see that

Consequently,

Hence, for  , there are
, there are

In view of assumption (H5), we have

It follows that

Therefore,  for
for  . So condition (C1) in Lemma 2.10 is satisfied.
. So condition (C1) in Lemma 2.10 is satisfied.
Finally, we show that (C3) in Lemma 2.10 holds. In fact, for  and
and  , we have
, we have

Thus by Lemma 2.10 and the assumption that  on
on  , BVPs (1.1)-(1.2) have at least three positive solutions. The proof is complete.
, BVPs (1.1)-(1.2) have at least three positive solutions. The proof is complete.
Theorem 3.2.
Suppose that there are positive numbers  ,
,  , and
, and  with
with  ,
,  , and
, and  such that (H3)-(H4) and the following condition are satisfied.
such that (H3)-(H4) and the following condition are satisfied.
(H6) for all
for all  , where
, where

Then BVPs (1.1)-(1.2) have at least three positive solutions.
Proof.
Let the nonnegative continuous convex functionals  ,
,  be defined on the cone
be defined on the cone  as Theorem 3.1 and the nonnegative continuous concave functional
as Theorem 3.1 and the nonnegative continuous concave functional  be defined on the cone
be defined on the cone  by
by

We will show that condition (C1) in Lemma 2.10 holds. Let  . We choose
. We choose  for
for  . It is easy to see that
. It is easy to see that

Consequently,

Hence, for  , there are
, there are

In view of assumption (H6), we have

It follows that

Therefore,  for
for  . So condition (C1) in Lemma 2.10 is satisfied. Using a similar proof to Theorem 3.1, the other conditions in Lemma 2.10 are satisfied. By Lemma 2.10, BVPs (1.1)-(1.2) have at least three positive solutions. The proof is complete.
. So condition (C1) in Lemma 2.10 is satisfied. Using a similar proof to Theorem 3.1, the other conditions in Lemma 2.10 are satisfied. By Lemma 2.10, BVPs (1.1)-(1.2) have at least three positive solutions. The proof is complete.
4. An Example
Example 4.1.
Consider the following second-order Laplacian dynamic equations on time scales

with integral boundary condition

where

Then BVPs (4.1)-(4.2) have at least three positive solutions.
Proof.
Take  ,
,  ,
,  ,
,  ,
,  , and
, and  . It follows that
. It follows that

From (4.1)-(4.2), it is easy to obtain

Hence, we have

Moreover, we have
(H3) for all  ,
,

(H4) for all  ,
,

(H5)for all  ,
,

Therefore, conditions (H3)–(H5) in Theorem 3.1 are satisfied. Further, it is easy to verify that the other conditions in Theorem 3.1 hold. By Theorem 3.1, BVPs (4.1)-(4.2) have at least three positive solutions. The proof is complete.
References
O'Regan D: Some general existence principles and results for
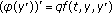 ,
,  . SIAM Journal on Mathematical Analysis 1993, 24(3):648–668. 10.1137/0524040
. SIAM Journal on Mathematical Analysis 1993, 24(3):648–668. 10.1137/0524040del Pino M, Drábek P, Manásevich R: The Fredholm alternative at the first eigenvalue for the one-dimensional p -Laplacian. Journal of Differential Equations 1999, 151(2):386–419. 10.1006/jdeq.1998.3506
Cabada A, Pouso RL: Existence results for the problem
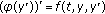 with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1999, 35(2):221–231. 10.1016/S0362-546X(98)00009-1
with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1999, 35(2):221–231. 10.1016/S0362-546X(98)00009-1Lü H, Zhong C: A note on singular nonlinear boundary value problems for the one-dimensional p -Laplacian. Applied Mathematics Letters 2001, 14(2):189–194. 10.1016/S0893-9659(00)00134-8
Feng W, Webb JRL: Solvability of three point boundary value problems at resonance. Nonlinear Analysis: Theory, Methods & Applications 1997, 30(6):3227–3238. 10.1016/S0362-546X(96)00118-6
Gupta CP: A non-resonant multi-point boundary-value problem for a p -Laplacian type operator. In Proceedings of the 5th Mississippi State Conference on Differential Equations and Computational Simulations (Mississippi State, MS, 2001), Electron. J. Differ. Equ. Conf.. Volume 10. Southwest Texas State University; 2003:143–152.
Tian Y, Ge W: Periodic solutions of non-autonomous second-order systems with a p -Laplacian. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(1):192–203. 10.1016/j.na.2005.11.020
Bohner M, Peterson A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston, Mass, USA; 2001:x+358.
Bohner M, Peterson A (Eds): Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston, Mass, USA; 2003:xii+348.
Agarwal RP, Bohner M, Li W-T: Nonoscillation and Oscillation: Theory for Functional Differential Equations, Monographs and Textbooks in Pure and Applied Mathematics. Volume 267. Marcel Dekker, New York, NY, USA; 2004:viii+376.
Sun H-R, Tang L-T, Wang Y-H: Eigenvalue problem for p -Laplacian three-point boundary value problems on time scales. Journal of Mathematical Analysis and Applications 2007, 331(1):248–262. 10.1016/j.jmaa.2006.08.080
Jiang L, Zhou Z: Existence of weak solutions of two-point boundary value problems for second-order dynamic equations on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(4):1376–1388. 10.1016/j.na.2007.06.034
Tian Y, Ge W: Existence and uniqueness results for nonlinear first-order three-point boundary value problems on time scales. Nonlinear Analysis: Theory, Methods & Applications 2008, 69(9):2833–2842. 10.1016/j.na.2007.08.054
Aykut Hamal N, Yoruk Fulya: Positive solutions of nonlinear m -point boundary value problems on time scales. Journal of Computational and Applied Mathematics 2009, 231(1):92–105. 10.1016/j.cam.2009.02.003
Sun H-R: Triple positive solutions for p -Laplacian m -point boundary value problem on time scales. Computers & Mathematics with Applications 2009, 58(9):1736–1741. 10.1016/j.camwa.2009.07.083
Yang Y, Meng F: Positive solutions of the singular semipositone boundary value problem on time scales. Mathematical and Computer Modelling 2010, 52(3–4):481–489. 10.1016/j.mcm.2010.03.045
Agarwal RP, Bohner M, Rehák P: Half-linear dynamic equations. In Nonlinear Analysis and Applications: To V. Lakshmikantham on His 80th Birthday. Volume 1. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2003:1–57.
Aulbach B, Neidhart L: Integration on measure chains. In Proceedings of the 6th International Conference on Difference Equations, Boca Raton, Fla, USA. CRC Press; 2004:239–252.
Bai Z, Ge W: Existence of three positive solutions for some second-order boundary value problems. Computers & Mathematics with Applications 2004, 48(5–6):699–707. 10.1016/j.camwa.2004.03.002
Acknowledgment
This work is supported the by the National Natural Sciences Foundation of China under Grant no. 10971183.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, Y., Zhang, T. Multiple Positive Solutions for Second-Order  -Laplacian Dynamic Equations with Integral Boundary Conditions.
Bound Value Probl 2011, 867615 (2011). https://doi.org/10.1155/2011/867615
-Laplacian Dynamic Equations with Integral Boundary Conditions.
Bound Value Probl 2011, 867615 (2011). https://doi.org/10.1155/2011/867615
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/867615
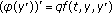 ,
,  . SIAM Journal on Mathematical Analysis 1993, 24(3):648–668. 10.1137/0524040
. SIAM Journal on Mathematical Analysis 1993, 24(3):648–668. 10.1137/0524040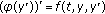 with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1999, 35(2):221–231. 10.1016/S0362-546X(98)00009-1
with nonlinear boundary conditions. Nonlinear Analysis: Theory, Methods & Applications 1999, 35(2):221–231. 10.1016/S0362-546X(98)00009-1