- Research
- Open access
- Published:
Existence of multiple positive solutions for fourth-order boundary value problems in Banach spaces
Boundary Value Problems volume 2012, Article number: 107 (2012)
Abstract
This paper deals with the positive solutions of a fourth-order boundary value problem in Banach spaces. By using the fixed-point theorem of strict-set-contractions, some sufficient conditions for the existence of at least one or two positive solutions to a fourth-order boundary value problem in Banach spaces are obtained. An example illustrating the main results is given.
MSC:34B15.
1 Introduction
In this paper, we consider the existence of multiple positive solutions for the fourth-order ordinary differential equation boundary value problem in a Banach space E
where is continuous, , θ is the zero element of E. This problem models deformations of an elastic beam in equilibrium state, whose two ends are simply supported. Owing to its importance in physics, the existence of this problem in a scalar space has been studied by many authors using Schauder’s fixed-point theorem and the Leray-Schauder degree theory (see [1–5] and references therein). On the other hand, the theory of ordinary differential equations (ODE) in abstract spaces has become an important branch of mathematics in last thirty years because of its application in partial differential equations and ODEs in appropriately infinite dimensional spaces (see, for example, [6–8]). For an abstract space, it is here worth mentioning that Guo and Lakshmikantham [9] discussed the multiple solutions of two-point boundary value problems of ordinary differential equations in a Banach space. Recently, Liu [10] obtained the sufficient condition for multiple positive solutions to fourth-order singular boundary value problems in an abstract space. In [11], by using the fixed-point index theory in a cone for a strict-set-contraction operator, the authors have studied the existence of multiple positive solutions for the singular boundary value problems with an integral boundary condition.
However, the above works in a Banach space were carried out under the assumption that the second-order derivative is not involved explicitly in the nonlinear term f. This is because the presence of second-order derivatives in the nonlinear function f will make the study extremely difficult. As a result, the goal of this paper is to fill up the gap, that is, to investigate the existence of solutions for fourth-order boundary value problems of (1.1) in which the nonlinear function f contains second-order derivatives, i.e., f depends on .
The main features of this paper are as follows. First, we discuss the existence results in an abstract space E, not . Secondly, we will consider the nonlinear term which is more extensive than the nonlinear term of [10, 11]. Finally, the technique for dealing with fourth-order BVP is completely different from [10, 11]. Hence, we improve and generalize the results of [10, 11] to some degree, and so, it is interesting and important to study the existence of positive solutions of BVP (1.1). The arguments are based upon the -positive operator and the fixed-point theorem in a cone for a strict-set-contraction operator.
The paper is organized as follows. In Section 2, we present some preliminaries and lemmas that will be used to prove our main results. In Section 3, various conditions on the existence of positive solutions to BVP (1.1) are discussed. In Section 4, we give an example to demonstrate our result.
2 Preliminaries
Let the real Banach space E with norm be partially ordered by a cone P of E, i.e., if and only if . P is said to be normal if there exists a positive constant N such that implies . We consider problem (1.1) in . Evidently, is a Banach space with norm and is a cone of the Banach space . In the following, is called a solution of problem (1.1) if it satisfies (1.1). x is a positive solution of (1.1) if, in addition, x is nonnegative and nontrivial, i.e., and for .
For a bounded set V in a Banach space, we denote by the Kuratowski measure of noncompactness (see [6–8] for further understanding). In this paper, we denote by the Kuratowski measure of noncompactness of a bounded set in E and in .
Lemma 2.1 [6]
Let and D be a bounded set, f be uniformly continuous and bounded from into E, then
The key tool in our approach is the following fixed-point theorem of strict-set-contractions:
Theorem 2.1 [8]
Let P be a cone of a real Banach space E and with . Suppose that is a strict set contraction such that one of the following two conditions is satisfied:
-
(i)
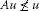 for , and for , ;
for , and for , ; -
(ii)
for , and
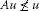 for , ;
for , ;
then the operator A has at least one fixed point such that .
The following concept is due to Krasnosel’skii [12, 13], with a slightly more general definition in [12].
Definition 2.1 We say that a bounded linear operator is -positive on a cone if there exists such that for every , there are positive constants , such that
Lemma 2.2 Let T be -positive on a cone K. If T is completely continuous, then , the spectral radius of T, is the unique positive eigenvalue of T with its eigenfunction in K. Moreover, if holds with , then for an arbitrary non-zero () the elements u and are incomparable

In the following, the closed balls in spaces E and are denoted, respectively, by () and ().
For convenience, let us list the following assumptions:
() , f is bounded and uniformly continuous in t on for any , and there exist two nonnegative constants , with such that
() There are three positive constants , , such that
for all and .
() There is a ( denotes the dual cone of P) with for any , two nonnegative constants , and a real number such that
for all and .
() There is a with for any and two nonnegative constants , and a real number such that
and .
() There are three positive constants , , such that
for all and .
() There exists such that
() There is a with and for any and a real number such that
where , .
Now, let be the Green’s function of the linear problem together with , which can be explicitly given by
Obviously, have the following properties:
Set
Obviously, is continuous.
Let . Since , we have
Using the above transformation and (2.2), BVP (1.1) becomes
with
From (2.3) and (2.4), we have
Now, define an operator A on Q by
The following Lemma 2.3 can be easily obtained.
Lemma 2.3 Assume that () holds. Then and
-
(i)
is continuous and bounded;
-
(ii)
BVP (1.1) has a solution in if and only if A has a fixed point in Q.
Let
It is easy to see that is a -positive operator with and .
Lemma 2.4 Suppose that () holds. Then for any , is a strict set contraction.
Proof For any and , by the expression of S, we have
and thus is continuous and bounded. By the uniformly continuous f and (), and Lemma 2.1, we have
Since f is uniformly continuous and bounded on , we see from (2.5) that A is continuous and bounded on . Let , according to (2.5), it is easy to show that the functions are uniformly bounded and equicontinuous, and so in [9] we have
where
Using the obvious formula
and observing , we find
where , .
From the fact of [9], we know
It follows from (2.6) and (2.7) that
and consequently, A is a strict set contraction on because . □
3 Main results
Theorem 3.1 Let a cone P be normal and condition () be satisfied. If () and () or () and () are satisfied, then BVP (1.1) has at least one positive solution.
Proof Set
It is clear that is a cone of the Banach space and . For any , by (2.1), we can obtain , then
We first assume that () and () are satisfied. Let
In the following, we prove that W is bounded.
For any , we have , that is, , . And so , set , by ()
For , let , then is a bounded linear operator. From (3.1), one deduces that
Since is the first eigenvalue of T, by (), the first eigenvalue of , . Therefore, by [14], the inverse operator exists and
It follows from that . So, we know that , and W is bounded.
Taking , we have
Next, we are going to verify that for any ,

If this is false, then there exists such that . This together with () yields
For , let , then the above inequality can be written in the form
It is easy to see that
In fact, implies for , and consequently, in contradiction to . Now, notice that is a -positive operator with , then by Lemma 2.2, we have for some . This together with and (3.4) implies that
which is a contradiction to . So, (3.3) holds.
By Lemma 2.4, A is a strict set contraction on . Observing (3.2) and (3.3) and using Theorem 2.1, we see that A has a fixed point on .
Next, in the case that () and () are satisfied, by the method as in establishing (3.3), we can assert from () that for any ,
Let
It is clear that is a completely continuous linear -operator with and in which . In addition, the spectral radius and is the positive eigenfunction of corresponding to its first eigenvalue .
Let
where . It is clear that is a completely continuous linear -operator with and . Thus, the spectral radius and has a positive eigenfunction corresponding to its first eigenvalue .
Take () satisfying and (). For , , we have
By [12], we have . Let , by Gelfand’s formula, we have . Let as .
In the following, we prove that .
Let be the positive eigenfunction of corresponding to , i.e.,
satisfying . Without loss of generality, by standard argument, we may suppose by the Arzela-Ascoli theorem and that as . Thus, and by (3.6), we have
that is, . This together with Lemma 2.2 guarantees that .
By the above argument, it is easy to see that there exists a such that
Choose
Now, we assert that

If this is not true, then there exists with such that , then . Moreover, by the definition of , we know
Thus, , , which implies by (3.7) we have
and
So, by (), we get
It is easy to see that
In fact, implies for , and consequently, in contradiction to . Now, notice that is a -positive operator with . Then by Lemma 2.2, we have for some , where is the positive eigenfunction of corresponding to . This together with implies that
which is a contradiction to . So, (3.8) holds.
By Lemma 2.4, A is a strict set contraction on . Observing (3.5) and (3.8) and using Theorem 2.1, we see that A has a fixed point on . This together with Lemma 2.3 implies that BVP (1.1) has at least one positive solution. □
Theorem 3.2 Let a cone P be normal. Suppose that conditions (), (), () and () are satisfied. Then BVP (1.1) has at least two positive solutions.
Proof We can take the same as in Theorem 3.1. As in the proof of Theorem 3.1, we can also obtain that . And we choose , with such that


On the other hand, it is easy to see that
In fact, if there exists with such that , then observing and , we get
and so
where, by virtue of (),
It follows from (3.12) and (3.13) that
a contradiction. Thus (3.11) is true.
By Lemma 2.4, A is a strict set contraction on , and also on . Observing (3.9), (3.10), (3.11) and applying, respectively, Theorem 2.1 to A, and , we assert that there exist and such that and and, by Lemma 2.3 and (3.11), , are positive solutions of BVP (1.1). □
Theorem 3.3 Let a cone P be normal. Suppose that conditions (), () and () and () are satisfied. Then BVP (1.1) has at least two positive solutions.
Proof We can take the same as in Theorem 3.1. As in the proof of Theorem 3.1, we can also obtain that . And we choose , with such that


On the other hand, it is easy to see that

In fact, if there exists with such that , then
Observing and , we get
which is a contradiction. Hence, (3.16) holds.
By Lemma 2.4, A is a strict set contraction on and also on . Observing (3.14), (3.15), (3.16) and applying, respectively, Theorem 2.1 to A, and , we assert that there exist and such that and and, by Lemma 2.3 and (3.16), , are positive solutions of BVP (1.1). □
4 One example
Now, we consider an example to illustrate our results.
Example 4.1 Consider the following boundary value problem of the finite system of scalar differential equations:
where


Claim (4.1) has at least two positive solutions and such that
Proof Let with the norm , and . Then P is a normal cone in E, and the normal constant is . System (4.1) can be regarded as a boundary value problem of (1.1) in E, where , ,
Evidently, is continuous. In this case, condition () is automatically satisfied. Since is identical zero for any and . Obviously, , so we may choose , then for any , we have
Noticing , we have
for all with and , and
for all with and . So, the conditions () and () are satisfied with and .
Choosing for and with , we have
So, condition () is satisfied. Thus, our conclusion follows from Theorem 3.2. □
References
Aftabizadeh AR: Existence and uniqueness theorems for fourth-order boundary value problems. J. Math. Anal. Appl. 1986, 116: 415-426. 10.1016/S0022-247X(86)80006-3
Yang Y: Fourth-order two-point boundary value problems. Proc. Am. Math. Soc. 1988, 104: 175-180. 10.1090/S0002-9939-1988-0958062-3
del Pino MA, Manasevich RF: Existence for a fourth-order boundary value problem under a two-parameter nonresonance condition. Proc. Am. Math. Soc. 1991, 112: 81-86.
Agarwal RP: On fourth-order boundary value problems arising in beam analysis. Differ. Integral Equ. 1989, 2: 91-110.
Cui Y, Zou Y: Existence and uniqueness theorems for fourth-order singular boundary value problems. Comput. Math. Appl. 2009, 58: 1449-1456. 10.1016/j.camwa.2009.07.041
Deimling K: Ordinary Differential Equations in Banach Spaces. Springer, Berlin; 1977.
Lakshmikantham V, Leela S: Nonlinear Differential Equations in Abstract Spaces. Pergamon, Oxford; 1981.
Guo D, Lakshmikantham V, Liu X: Nonlinear Integral Equations in Abstract Spaces. Kluwer Academic, Dordrecht; 1996.
Guo D, Lakshmikantham V: Multiple solutions of two-point boundary value problem of ordinary differential equations in Banach space. J. Math. Anal. Appl. 1988, 129: 211-222. 10.1016/0022-247X(88)90243-0
Liu Y: Multiple positive solutions to fourth-order singular boundary value problems in abstract space. Electron. J. Differ. Equ. 2004, 120: 1-13.
Zhang X, Feng M, Ge W: Existence results for nonlinear boundary value problems with integral boundary conditions in Banach spaces. Nonlinear Anal. 2008, 69: 3310-3321. 10.1016/j.na.2007.09.020
Krasnosel’skii MA: Positive Solutions of Operator Equations. Noordhoff, Groningen; 1964.
Krasnosel’skii MA, Zabreiko PP: Geometrical Methods of Nonlinear Analysis. Springer, Berlin; 1984.
Xia D, Wu Z, Yan S, Shu W: Theory of Real Variable Functions and Functional Analysis. 2nd edition. Higher Education Press, Beijing; 1985.
Acknowledgements
The authors would like to thank the referees for carefully reading this article and making valuable comments and suggestions. This work is supported by the Foundation items: NSFC (10971179), NSF (BS2010SF023, BS2012SF022) of Shandong Province.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors typed, read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cui, Y., Sun, J. Existence of multiple positive solutions for fourth-order boundary value problems in Banach spaces. Bound Value Probl 2012, 107 (2012). https://doi.org/10.1186/1687-2770-2012-107
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2012-107
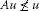 for , and for , ;
for , and for , ;