- Research
- Open access
- Published:
Existence and uniqueness of positive solution to singular fractional differential equations
Boundary Value Problems volume 2012, Article number: 81 (2012)
Abstract
In this paper, we discuss the existence and uniqueness of a positive solution to the following singular fractional differential equation with nonlocal boundary value conditions:
where , , with , is the standard Riemann-Liouville derivative, f may be singular at , , and .
MSC:34B10, 34B15.
1 Introduction
In this paper, we consider the following fractional differential equation:
where , , with , is the standard Riemann-Liouville derivative, may be singular at , , and . In this paper, by a positive solution to (1.1), we mean a function which satisfies , positive on and satisfies (1.1).
Recently, many results were obtained dealing with the existence of solutions for nonlinear fractional differential equations by using the techniques of nonlinear analysis; see [1–23] and references therein. The multi-point boundary value problems (BVP for short) have provoked a great deal of attention, for example [13–19]. In [10], the authors discussed some positive properties of the Green function for Direchlet-type BVP of nonlinear fractional differential equation
where , is the standard Riemann-Liouville derivative, . By using the Krasnosel’skii fixed point theorem, the existence of positive solutions were obtained under suitable conditions on f.
In [14], the authors investigated the existence and multiplicity of positive solutions by using some fixed point theorems for the fractional differential equation
where , , , with , , satisfied Carathéodory type conditions.
In [20, 21], the authors considered the fractional differential equation given by
In order to obtain the existence of positive solutions of (1.4), they considered the following fractional differential equation:
In [20], , and g, h have different monotone properties. By using the fixed point theorem for the mixed monotone operator, Zhang obtained (1.4) and had a unique positive solution with . But the results are not true since is a positive solution of (1.5), and . What causes it lies in the unsuitable using of properties of the Green function.
In [21], , is increasing for , . By using the positive properties of the Green function obtained in and fixed point theory for the concave operator, the authors obtained the uniqueness of a positive solution for the BVP (1.4).
Motivated by the works mentioned above, in this paper we aim to establish the existence and uniqueness of a positive solution to the BVP (1.1). Our work presented in this paper has the following features. Firstly, the BVP (1.1) possesses singularity, that is, f may be singular at , , and . Secondly, we impose weaker positivity conditions on the nonlocal boundary term, that is, some of the coefficients can be negative. Thirdly, the unique positive solution can be approximated by an iterative scheme.
The rest of the paper is organized as follows. In Section 2, we present some preliminaries and lemmas that will be used to prove our main results. We also develop some new positive properties of the Green function. In Section 3, we discuss the existence and uniqueness of a positive solution of the BVP (1.1), we also give an example to demonstrate the application of our theoretical results.
2 Preliminaries
For the convenience of the reader, we present here the necessary definitions from fractional calculus theory. These definitions can be found in recent literature.
Definition 2.1 The fractional integral of order of a function is given by
provided the right-hand side is defined pointwise on .
Definition 2.2 The fractional derivative of order of a continuous function is given by
where , denotes the integral part of the number α, provided the right-hand side is pointwisely defined on .
Definition 2.3 By , we mean .
Lemma 2.1 ([3])
Let . Then the following equality holds for , ,
where , , .
Set



where
For the convenience in presentation, we here list the assumption to be used throughout the paper.
() , on .
Remark 2.1 If (), we have and . If () and , we have and on .
Lemma 2.2 ([14])
Assume that and . Then
Lemma 2.3 Assume () holds, and . Then the unique solution of the problem
is
where is called the Green function of BVP (2.5).
Proof From Lemma 2.1, we have the solution of (2.5) given by
Consequently,
From , we have .
By Lemma 2.2, we have
Therefore,
and
By , we have
Therefore, the solution of (2.5) is
□
Lemma 2.4 The function has the following properties:
-
(1)
, for ;
-
(2)
, for ;
-
(3)
, for , where
(2.6)
Proof It is obvious that (1), (2) hold. In the following, we will prove (3).
-
(i)
When , noticing , we have
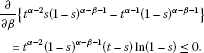 (2.7)
(2.7)
Therefore,
which implies
On the other hand, we have
Therefore, , which implies
Then
-
(ii)
When , we have
(2.10)
On the other hand, clearly we have
(2.8)-(2.11) implies (3) holds. □
By Lemma 2.4 we have the following results.
Lemma 2.5 Assume () holds, then the Green function defined by (2.3) satisfies:
-
(1)
, ;
-
(2)
, ;
-
(3)
, , where
Lemma 2.6 Assume () holds, then the function satisfies:
-
(1)
, ;
-
(2)
, ;
-
(3)
, .
For convenience, we list here two more assumptions to be used later:
() , here , is nondecreasing on u, nonincreasing on v, and there exists such that
()
Remark 2.2 Inequality (2.12) is equivalent to
Let be endowed with the maximum norm . Define a cone P by
Let
Set , where θ is the zero element of E. We have the following lemma.
Lemma 2.7 Suppose that ()-() hold. Then .
Proof For any , there exists , such that
By (), () and (2) of Lemma 2.6, we get
where . This implies that A is well defined in .
On the other hand, by (3) of Lemma 2.6, we have

Therefore, . Combining with (2.16), we have . □
Remark 2.3 By () and (2.15), A is a mixed monotone operator.
3 Main results
Theorem 3.1 Suppose that ()-() hold. Then the BVP (1.1) has a unique positive solution.
Proof For any , by Remark 2.2, we have
For any , noticing , we can choose small enough such that
Set
Clearly,
Let
It is easy to see that
Noticing
therefore,
Suppose that , then , and
By induction, we can get
By (3.4), (3.5), we have
which implies is a Cauchy sequence. Similarly, is a Cauchy sequence. Noticing (3.4), there exist , such that converges to and converges to . Moreover,
(3.5) and (3.6) imply that
This implies that .
By the mixed monotone property of A and (3.6), we have
Let , we get
Since , we have is a positive fixed point of A.
In the following, we will prove the positive fixed point of A is unique.
Suppose is a positive fixed point of A. By Lemma 2.6, we can get . Let
Then , and . Therefore
Thus, , which contradicts the definition of . Consequently, the positive fixed point of A is unique.
It is clear that satisfies
On the other hand, since , we have . Then, . By Lemma 2.5 and (), (), we can get . Moreover,
Lemma 2.3 implies is a positive solution of (1.1).
On the other hand, if is a positive solution of (1.1), then
By Lemma 2.5, we have there exists such that
Set , we have
and
which implies u is a positive fixed point of A.
Then is the unique positive solution of the BVP (1.1). □
Remark 3.1 The unique positive solution y of (1.1) can be approximated by the iterative schemes: for any , let , be defined as (3.2) and , , , then .
Example 3.1 (A 4-point BVP with coefficients of both signs)
Consider the following problem:
with
Then
and
By direct calculations, we have and , which implies () holds.
Let
Obviously, , is nondecreasing on x and nonincreasing on y. It is easy to see that
Then
Therefore () holds. It is easy to get that () holds. Therefore, the assumptions of Theorem 3.1 are satisfied. Thus Theorem 3.1 ensures that the BVP (3.8) has a unique positive solution.
References
Samko SG, Kilbas AA, Marichev OI: Fractional Integral and Derivatives (Theory and Applications). Gordon & Breach, Switzerland; 1993.
Podlubny I Mathematics in Science and Engineering 198. In Fractional Differential Equations. Academic Press, New York; 1999.
Kilbas AA, Srivastava HM, Trujillo JJ: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam; 2006.
Agrawal OP: Formulation of Euler-Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 2002, 272: 368-379. 10.1016/S0022-247X(02)00180-4
Lakshmikantham V, Vatsala AS: General uniqueness and monotone iterative technique for fractional differential equations. Appl. Math. Lett. 2008, 21: 828-834. 10.1016/j.aml.2007.09.006
Kosmatov N: Integral equations and initial value problems for nonlinear differential equations of fractional order. Nonlinear Anal. 2009, 70: 2521-2529. 10.1016/j.na.2008.03.037
Agarwal RP, O’Regan D, Stanek S: Positive solutions for Dirichlet problem of singular nonlinear fractional differential equations. J. Math. Anal. Appl. 2010, 371: 57-68. 10.1016/j.jmaa.2010.04.034
Ahmad B, Alsaedi A: Existence of solutions for anti-periodic boundary value problems of nonlinear impulsive functional integro-differential equations of mixed type. Nonlinear Anal. 2009, 3: 501-509.
Liang S, Zhang J: Positive solutions for boundary value problems of fractional differential equation. Nonlinear Anal. 2009, 71: 5545-5550. 10.1016/j.na.2009.04.045
Jiang D, Yuan C: The positive properties of the Green function for Dirichlet-type boundary value problems of nonlinear fractional differential equations and its application. Nonlinear Anal. 2010, 72: 710-719. 10.1016/j.na.2009.07.012
Goodrich CS: Existence of positive solution to a class of fractional differential equations. Appl. Math. Lett. 2010, 23: 1050-1055. 10.1016/j.aml.2010.04.035
Arara A, Benchohra M, Hamidi N, Nieto JJ: Fractional order differential equations on an unbounded domain. Nonlinear Anal. 2010, 72: 580-586. 10.1016/j.na.2009.06.106
Salem HAH: On the fractional order m -point boundary value problem in reflexive Banach spaces and weak topologies. Comput. Math. Appl. 2009, 224: 565-572. 10.1016/j.cam.2008.05.033
Li CF, Luo XN, Zhou Y: Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations. Comput. Math. Appl. 2010, 59: 1363-1375. 10.1016/j.camwa.2009.06.029
Benchohraa M, Hamania S, Ntouyas SK: Boundary value problems for differential equations with fractional order and nonlocal conditions. Nonlinear Anal. 2009, 71: 2391-2396. 10.1016/j.na.2009.01.073
El-Shahed M, Nieto JJ: Nontrivial solutions for a nonlinear multi-point boundary value problem of fractional order. Comput. Math. Appl. 2010, 59: 3438-3443. 10.1016/j.camwa.2010.03.031
Bai Z: On positive solutions of a nonlocal fractional boundary value problem. Nonlinear Anal. 2010, 72: 916-924. 10.1016/j.na.2009.07.033
Rehman M, Khan RA: Existence and uniqueness of solution for multi-point boundary value problems for fractional differential equations. Appl. Math. Lett. 2010, 23: 1038-1044. 10.1016/j.aml.2010.04.033
Allison J, Kosmatov N: Multi-point boundary value problems of fractional order. Commun. Appl. Anal. 2008, 12(4):451-458.
Zhang S: Positive solution to singular boundary value problem for nonlinear fractional differential equation. Comput. Math. Appl. 2010, 59: 1300-1309. 10.1016/j.camwa.2009.06.034
Yang L, Chen H: Unique positive solutions for fractional differential equation boundary value problems. Appl. Math. Lett. 2010, 23: 1095-1098. 10.1016/j.aml.2010.04.042
Chang Y, Kavitha V, Mallika Arjunan M: Existence and uniqueness of mild solutions to a semilinear integrodifferential equation of fractional order. Nonlinear Anal. 2009, 71: 5551-5559. 10.1016/j.na.2009.04.058
Shua X, Lai Y, Chen Y: The existence of mild solutions for impulsive fractional partial differential equations. Nonlinear Anal. 2011, 74: 2003-2011. 10.1016/j.na.2010.11.007
Acknowledgements
The authors are grateful to the anonymous referee for his/her valuable suggestions. The first and second authors were supported financially by the National Natural Science Foundation of China (11071141, 11126231) and Project of Shandong Province Higher Educational Science and Technology Program (J11LA06). The third author was supported financially by the Australia Research Council through an ARC Discovery Project Grant.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors declare that the study was realized in collaboration with the same responsibility. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, Y., Liu, L. & Wu, Y. Existence and uniqueness of positive solution to singular fractional differential equations. Bound Value Probl 2012, 81 (2012). https://doi.org/10.1186/1687-2770-2012-81
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2012-81