- Research
- Open access
- Published:
Existence of positive solutions of elliptic mixed boundary value problem
Boundary Value Problems volume 2012, Article number: 91 (2012)
Abstract
In this paper, we use variational methods to prove two existence of positive solutions of the following mixed boundary value problem:
One deals with the asymptotic behaviors of near zero and infinity and the other deals with superlinear of at infinity.
MSC:35M12, 35D30.
1 Introduction and preliminaries
This paper is concerned with the existence of positive solutions of the following elliptic mixed boundary value problem:
where Ω is a bounded domain in with Lipschitz boundary ∂ Ω, , , Γ is a sufficiently smooth -dimensional manifold, and ν is the outward normal vector on ∂ Ω. We assume , are continuous and satisfy
(S1) , , , . , , .
(S2) For almost every , is nondecreasing with respect to .
(S3) , uniformly in a.e. , where , is the first eigenvalue of (2), , .
(S4) There exists such that for some as and as .
The eigenvalue problem of (1) is studied by Liu and Su in [1]
There exists a set of eigenvalues and corresponding eigenfunctions which solve problem (2), where , as , .
There have been many papers concerned with similar problems at resonance under the boundary condition; see [2–10]. Moreover, some multiplicity theorems are obtained by the topological degree technique and variational methods; interested readers can see [11–17]. Problem (1) is different from the classical ones, such as those with Dirichlet, Neuman, Robin, No-flux, or Steklov boundary conditions.
In this paper, we assume is a closed subspace of . We define the norm in V as , is the norm, is the norm, is the trace operator with for all , that is continuous and compact (see [18]). Furthermore, we define , for (see [1]). Then, by (S3), we obtain
Let Ω be a bounded domain with a Lipschitz boundary; there is a continuous embedding for when , and when . Then there exists , such that
Moreover, there is a continuous boundary trace embedding for when , and when . Then there exists , such that
It is well known that to seek a nontrivial weak solution of problem (1) is equivalent to finding a nonzero critical value of the functional
where , , . Moreover, by (S1) and the Strong maximum principle, a nonzero critical point of J is in fact a positive solution of (1). In order to find critical points of the functional (6), one often requires the technique condition, that is, for some , , ,
It is easy to see that the condition (AR) implies that , that is, must be superlinear with respect to u at infinity. In the present paper, motivated by [19] and [20], we study the existence and nonexistence of positive solutions for problem (1) with the asymptotic behavior assumptions (S3) of f at zero and infinity. Moreover, we also study superlinear of f at infinity with in (S3), which is weaker than the (AR) condition, that is the (AR) condition does not hold.
In order to get our conclusion, we define the minimization problem
then , which is achieved by some with a.e. in Ω; see Lemma 1.
We denote by c, , universal constants unless specified otherwise. Our main results are as follows.
Theorem 1 Let conditions (S 1) to (S 3) hold, then:
-
(i)
If , then the problem (1) has no any positive solution in V.
-
(ii)
If , then the problem (1) has at least one positive solution in V.
-
(iii)
If , then the problem (1) has one positive solution if and only if there exists a constant such that and , a.e. , where is the function which achieves Λ.
Corollary 2 Let conditions (S 1) to (S 3) with hold, then:
-
(i)
If , then the problem (1) has no any positive solution in V.
-
(ii)
If , then the problem (1) has at least one positive solution in V.
-
(iii)
If , then the problem (1) has one positive solution if and only if there exists a constant such that and , a.e. , where is the eigenfunction of the .
Theorem 3 Let conditions (S 1) to (S 4) with hold, then the problem (1) has at least one positive solution in V.
2 Some lemmas
We need the following lemmas.
Lemma 1 If , , , then and there exists such that and . Moreover, a.e. in V.
Proof By the Sobolev embedding function and Fatou’s lemma, it is easy to know that and there exists , which satisfies Λ, that is, . Furthermore, we assume , then could replace by . By the Strong maximum principle, we know a.e. in V. □
Lemma 2 If conditions (S 1) to (S 3) hold, then there exists such that , , .
Proof By condition (S3), there exists , such that , as . Which implies that , .
By (4) and (5), we obtain
Hence, ; we take ε which satisfies , that is, . Then we take a positive constant β such that as , and is small enough. □
Lemma 3 If conditions (S 1) to (S 3) hold, , is defined by Lemma 1, then as .
Proof If , is defined by Lemma 1, by Fatou’s lemma, and (S3), we have

So, as . □
Lemma 4 Let conditions (S 1) and (S 2) hold. If a sequence satisfies as , then there exists a subsequence of , still denoted by such that for all , .
Proof Since as , for a subsequence, we may assume that
For any fixed and , set
Then (S2) implies that
It implies that , . Following the same procedures, we obtain , .
For all and positive integer n, by (8), we have
On the other hand, by (8), one has
One has
Combining (9) and (10), we have . □
Lemma 5 (see [21])
Suppose E is a real Banach space, satisfies the following geometrical conditions:
-
(i)
; there exists such that ;
-
(ii)
There exists such that . Let be the set of all continuous paths joining 0 and e:
and
Then there exists a sequence such that and .
3 Proofs of main results
Proof of Theorem 1 (i) If is one positive solution of problem (1), by (3), one has
That is,
It implies that . This completes the proof of Theorem 1(i).
-
(ii)
By Lemma 2, there exists such that with . By Lemma 3, we obtain as . Define
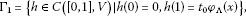 (11)
(11)

where is given by Lemma 1. Then and by Lemma 3, there exists such that


-
(14)
implies that
(15)
Here, in what follows, we use to denote any quantity which tends to zero as .
If is bounded in V, when Ω is bounded and , are subcritical, we can get has a subsequence strong convergence to a critical value of J, and our proof is complete. So, to prove the theorem, we only need show that is bounded in V. Supposing that is unbounded, that is, as . We order
Then is bounded in V. By extracting a subsequence, we suppose is a strong convergence in , is a convergence a.e. , is a weak convergence in V.
We claim that . In fact, by (S1) and (S3), we know , , and there exists such that , . If , is a strong convergence in , and by (15) and (16) we know
It is contradiction with , so .
As follows, we prove satisfies
We order

By (S1) and (S3), there exists such that , , . We select a suitable subsequence and there exists , such that is a strong convergence in , is a strong convergence in , and , , .
It follows from is a strong convergence in that

Hence, is bounded in , in ; is bounded in , in .
By (16), we have

Since is a weak convergence in V, we obtain
We order ; this yields , so . By the Strong maximum principle, we know a.e. in Ω, so a.e. in Ω. Combining (S3) and (3), we obtain
This is a contradiction with . This completes the proof of Theorem 1(ii).
-
(iii)
If , by Lemma 1, there exists some , such that
(17)
If u is a positive solution of (1), for the above , we have
We order in (17), and it follows from (18) that
which implies that .
When a.e. in Ω, combining (S2), (S3), and (3), we obtain
Then we must have , a.e. in Ω, also achieves Λ (=1). When , , we have , which achieves Λ.
On the other hand, if for some , and , a.e. , since also achieves Λ. This means is a solution of problem (1) as . This completes the proof of Theorem 1(iii). □
Proof of Corollary 2 Note that when , then . The conclusion follows from Theorem 1. □
Proof of Theorem 3 When , we can replace by in (11) and define c as in (12), then following the same procedures as in the proof of Theorem 1(ii), we need to show only that is bounded in V. For this purpose, let be defined as in (16). If is bounded in V, we know is a strong convergence in , is convergence a.e. , is a weak convergence in V, and .
If , then and . We set , . Obviously, by (16), a.e. in . When in (S3), there exists and n large enough we have , uniformly in . Hence, by (15) and (16), we obtain
Noticing that in and , can be chosen large enough, so and then in Ω.
Then we know , and consequently,
By , as , then it follows Lemma 4 and (13), we obtain
Obviously, (19) and (20) are contradictory. So is bounded in V. This completes the proof of Theorem 3. □
4 Example
In this section, we give two examples on : One satisfies (S1) to (S3) with , but does not satisfy the (AR) condition; the other illustrates how the assumptions on the boundary are not trivial and compatible with the inner assumptions in Ω.
Example 1 Set:
Then it is easy to verify that satisfies (S1) to (S3) with as and as . In addition,
So, for some , , for all t large.
This means does not satisfy the (AR) condition.
Example 2 Consider the following problem:
where is a constant. It is obvious that as . Problem (21) is a case of (1); we can obtain the nontrivial solution: , .
Author’s contributions
Li G carried out all studies in this article.
References
Liu H, Su N: Well-posedness for a class of mixed problem of wave equations. Nonlinear Anal. 2009, 71: 17-27. doi:10.1016/j.na.2008.10.027
Landesman EM, Lazer AC: Nonlinear perturbations of linear elliptic boundary value problems at resonance. J. Math. Mech. 1970, 19: 609-623.
Ahmad S, Lazer AC, Paul JL: Elementary critical point theory and perturbations of elliptic boundary value problems at resonance. Indiana Univ. Math. J. 1976, 25: 933-944. 10.1512/iumj.1976.25.25074
Berestycki H, De Figueiredo DG: Double resonance in semilinear elliptic problems. Commun. Partial Differ. Equ. 1981, 6: 91-120. 10.1080/03605308108820172
Costa DG, Oliveira AS: Existence of solution for a class of semilinear elliptic problems at double resonance. Bol. Soc. Bras. Mat. 1988, 19: 21-37. 10.1007/BF02584819
Omari P, Zanolin F: Resonance at two consecutive eigenvalues for semilinear elliptic equations. Ann. Mat. Pura Appl. 1993, 163: 181-198. 10.1007/BF01759021
Binding PA, Drábek P, Huang YX: Existence of multiple solutions of critical quasilinear elliptic Neumann problems. Nonlinear Anal. 2000, 42: 613-629. doi:10.1016/S0362-546X(99)00118-2 10.1016/S0362-546X(99)00118-2
Li G, Zhou HS: Asymptotically linear Dirichlet problem for the p -Laplacian. Nonlinear Anal. 2001, 43: 1043-1055. doi:10.1016/S0362-546X(99)00243-6 10.1016/S0362-546X(99)00243-6
Escobar JF: A comparison theorem for the first non-zero Steklov eigenvalue. J. Funct. Anal. 2000, 178: 143-155. doi:10.1006/jfan.2000.3662 10.1006/jfan.2000.3662
Kaur BS, Sreenadh K: Multiple positive solutions for a singular elliptic equation with Neumann boundary condition in two dimensions. Electron. J. Differ. Equ. 2009, 43: 1-13.
Ahmad S: Multiple nontrivial solutions of resonant and nonresonant asymptoticaly problems. Proc. Am. Math. Soc. 1986, 96: 405-409. 10.1090/S0002-9939-1986-0822429-2
Chang KC: Infinite Dimensional Morse Theory and Multiple Solutions Problems. Birkhäuser, Boston; 1993.
Hirano N, Nishimura T: Multiplicity results for semilinear elliptic problems at resonance and with jumping nonlinearities. J. Math. Anal. Appl. 1993, 180: 566-586. doi:10.1006/jmaa.1993.1417 10.1006/jmaa.1993.1417
Landesman E, Robinson S, Rumbos A: Multiple solution of semilinear elliptic problem at resonance. Nonlinear Anal. 1995, 24: 1049-1059. doi:10.1016/0362-546X(94)00107-S 10.1016/0362-546X(94)00107-S
Liu SQ, Tang CL, Wu XP: Multiplicity of nontrivial solutions of semilinear elliptic equations. J. Math. Anal. Appl. 2000, 249: 289-299. doi:10.1006/jmaa.2000.6704 10.1006/jmaa.2000.6704
Li S, Willem M: Multiple solution for asymptotically linear boundary value problems in which the nonlinearity crosses at least one eigenvalue. Nonlinear Differ. Equ. Appl. 1998, 5: 479-490. 10.1007/s000300050058
Mawhin J, Willem M: Critical Point Theory and Hamiltonien Systems. Springer, New York; 1989.
Lions JL, Magenes E: Non-Homogeneous Boundary Value Problems and Applications. Springer, Berlin; 1972.
Zhou H: An application of a mountain pass theorem. Acta Math. Sin. Engl. Ser. 2002, 18(1):27-36. 10.1007/s101140100147
Cheng BT, Wu X: Existence results of positive solutions of Kirchhoff type problems. Nonlinear Anal. 2009, 71: 4883-4892. doi:10.1016/j.na.2009.03.065 10.1016/j.na.2009.03.065
Ambrosetti A, Rabinowitz PH: Dual variational methods in critical points theory and applications. J. Funct. Anal. 1973, 14: 349-381. doi:10.1016/0022-1236(73)90051-7 10.1016/0022-1236(73)90051-7
Acknowledgements
The author would like to thank the referees for carefully reading this article and making valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that he has no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, G. Existence of positive solutions of elliptic mixed boundary value problem. Bound Value Probl 2012, 91 (2012). https://doi.org/10.1186/1687-2770-2012-91
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2012-91