- Research
- Open access
- Published:
First-order nonlinear differential equations with state-dependent impulses
Boundary Value Problems volume 2013, Article number: 195 (2013)
Abstract
The paper deals with the state-dependent impulsive problem
where , , f fulfils the Carathéodory conditions on , the impulse function 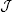 is continuous on , the barrier function γ has a continuous first derivative on some subset of ℝ and ℓ is a linear bounded functional which is defined on the Banach space of left-continuous regulated functions on equipped with the sup-norm. The functional ℓ is represented by means of the Kurzweil-Stieltjes integral and covers all linear boundary conditions for solutions of first-order differential equations subject to state-dependent impulse conditions. Here, sufficient and effective conditions guaranteeing the solvability of the above problem are presented for the first time.
is continuous on , the barrier function γ has a continuous first derivative on some subset of ℝ and ℓ is a linear bounded functional which is defined on the Banach space of left-continuous regulated functions on equipped with the sup-norm. The functional ℓ is represented by means of the Kurzweil-Stieltjes integral and covers all linear boundary conditions for solutions of first-order differential equations subject to state-dependent impulse conditions. Here, sufficient and effective conditions guaranteeing the solvability of the above problem are presented for the first time.
MSC:34B37, 34B15.
1 Introduction
The investigation of impulsive differential equations has a long history; see, e.g., the monographs [1–3]. Most papers dealing with impulsive differential equations subject to boundary conditions focus their attention on impulses at fixed moments. But this is a very particular case of a more complicated case with state-dependent impulses. Boundary value problems with state-dependent impulses, where difficulties with an operator representation appear (cf. Remark 6.2), are substantially less developed. We refer to the papers [4–6] and [7] which are devoted to periodic problems, and for problems with other boundary conditions, see [8, 9] or [10–12].
Here, in our paper, we present an approach leading to a new existence principle for impulsive boundary value problems. This approach is applicable to each linear boundary condition which is considered with some first-order differential equation subject to state-dependent impulses. The important step is a proof of a transversality (Remark 2.3 and Lemmas 5.1 and 5.2), which makes possible a construction of a continuous operator (Section 6) whose fixed point leads to a solution of our original impulsive problem (Section 7).
Notation
Let , , .
-
is the set of real functions continuous on M.
-
is the set of real functions absolutely continuous on M.
-
is the set of real functions Lebesgue integrable on .
-
is the set of real functions essentially bounded on .
-
is the set of real functions with bounded variation on .
-
is the set of real left-continuous regulated functions on , that is, if and only if , and for each and each ,
(1.1) -
is the set of functions such that
-
(i)
is measurable for all ,
-
(ii)
is continuous for a.e. ,
-
(iii)
for each compact set , there exists satisfying
-
The set equipped with the norm
(1.2)
is a Banach space.
-
Since , we equip the sets and with the norm and get also Banach spaces (cf.[13]). Then (1.2) can be written as
(1.3)
and
-
is the Banach space of functions such that and , where the norm is given by
(1.5) -
is the characteristic function of a set A, where .
2 Formulation of problem
We investigate the solvability of the nonlinear differential equation
subject to the state-dependent impulse condition
and the general linear boundary condition
Here we assume that
and is a linear bounded functional.
Definition 2.1 A function is a solution of problem (2.1), (2.2) if
-
there exists a unique such that ;
-
the restrictions and are absolutely continuous;
-
;
-
z satisfies equation (2.1) for a.e. .
Definition 2.2 A graph of a function is called a barrier γ.
Remark 2.3 Let  be the set of all solutions of problem (2.1), (2.2). According to Definition 2.1, each function satisfies a transversality property, which means that the graph of z crosses a barrier γ at a unique point , where the impulse
be the set of all solutions of problem (2.1), (2.2). According to Definition 2.1, each function satisfies a transversality property, which means that the graph of z crosses a barrier γ at a unique point , where the impulse 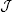 acts on z. After that (for ) the graph of z lies on the right of the barrier γ. This transversality property follows from transversality conditions (cf. (4.5), (4.6)) and it is proved in Section 5.
acts on z. After that (for ) the graph of z lies on the right of the barrier γ. This transversality property follows from transversality conditions (cf. (4.5), (4.6)) and it is proved in Section 5.
Assume that and . Then there exists a unique such that for and can occur. Therefore different functions from  can have their discontinuities at different points from . Our aim in this paper is to prove the existence of a solution of problem (2.1), (2.2) satisfying the general linear boundary condition (2.3). To do this, we need a suitable linear space containing
can have their discontinuities at different points from . Our aim in this paper is to prove the existence of a solution of problem (2.1), (2.2) satisfying the general linear boundary condition (2.3). To do this, we need a suitable linear space containing  . Due to state-dependent impulses, the Banach space of piece-wise continuous functions on with the sup-norm cannot be used here. Therefore we choose the Banach space . Clearly, by (1.1), . The operator ℓ in the general linear boundary condition (2.3) can be written uniquely in the form
. Due to state-dependent impulses, the Banach space of piece-wise continuous functions on with the sup-norm cannot be used here. Therefore we choose the Banach space . Clearly, by (1.1), . The operator ℓ in the general linear boundary condition (2.3) can be written uniquely in the form
where , and is the Kurzweil-Stieltjes integral (cf. [14], Theorem 3.8). Representation (2.5) is correct on  , because for each the integral exists. Its definition and properties can be found in [15] (see Perron-Stieltjes integral based on the work of Kurzweil).
, because for each the integral exists. Its definition and properties can be found in [15] (see Perron-Stieltjes integral based on the work of Kurzweil).
Definition 2.4 A function is a solution of problem (2.1)-(2.3) if z is a solution of problem (2.1), (2.2) and fulfils (2.3).
3 Green’s function
For further investigation, we will need a linear homogeneous problem corresponding to problem (2.1)-(2.3). Such problem has the form
because the impulse in (2.2) disappears if . We will also work with the non-homogeneous equation
where .
Definition 3.1 A solution of problem (3.3), (3.2) is a function satisfying equation (3.3) for a.e. and fulfilling condition (3.2).
Remark 3.2 If x is a solution of problem (3.3), (3.2), then x belongs to , and consequently condition (3.2) can be written in the form (cf. (2.5))
where , and the Lebesgue integral is used.
Definition 3.3 A function is the Green’s function of problem (3.1), (3.2) if
-
(i)
for any , the restrictions , are solutions of equation (3.1) and , where ;
-
(ii)
for any ;
-
(iii)
for any , the function
(3.5)
fulfils condition (3.4).
Lemma 3.4 Let ℓ be from (2.5) with and .
-
(i)
if and only if there exists the Green’s function G of problem (3.1), (3.2) which has the form
(3.6) -
(ii)
if and only if there exists a unique solution x of problem (3.3), (3.4), which has a form of (3.5) with G from (3.6).
Proof Clearly, G given by (3.6) fulfils (i) and (ii) of Definition 3.3 if and only if . A general solution of equation (3.3) is , where . By (3.4),
The equation
has a unique solution c if and only if . Then a unique solution x of problem (3.3), (3.4) is written as
□
Lemma 3.5 Let G be the Green’s function of problem (3.1), (3.2), where ℓ is from (2.5) and . Then, for each , the function belongs to and
Proof Choose . By (3.6),
Consequently, the function belongs to . This yields that the integral exists for each . Note that since is not continuous on , formula (3.4) cannot be used for in place of x. Instead, we use the properties of the Kurzweil-Stieltjes integral which justify the following computation
Hence, by (2.5), we get
□
Example 3.6 Consider a solution x of problem (3.3), (3.2), where ℓ has a form of the two-point boundary condition
We will show that ℓ can be expressed in a form of (3.4). If , then k and v can be found from the equality
Assuming that , we get
and hence , . In addition, if , then (cf. (3.6))
Example 3.7 Consider a solution x of problem (3.3), (3.2), where ℓ has a form of the multi-point boundary condition
Here . If , then k and v of (3.4) can be found from the equality
Assume that v is a piece-wise constant right-continuous function on , that is,
where , . By (3.10), we get
Consequently,
To summarize, if , then
and further (cf. (3.6))
Example 3.8 Consider a solution x of problem (3.3), (3.2), where ℓ has a form of the integral condition
where . If , then k and v of (3.4) can be found from the equality
Let us put
Then
and (3.11) gives , . Consequently,
Similarly, if
and , we derive
In both cases, G is written as
4 Assumptions
An existence result for problem (2.1)-(2.3) will be proved in the next sections under the basic assumption (2.4) and the following additional assumptions imposed on f, ℓ, 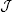 and γ.
and γ.
-
(i)
Boundedness of f
(4.1) -
(ii)
Boundedness of
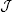 (4.2)
(4.2) -
(iii)
Boundedness of γ
(4.3) -
(iv)
Properties of ℓ
(4.4) -
(v)
Transversality conditions
(4.5)
where h is from (4.1) and , are from (4.3).
-
(vi)
-continuity of f
(4.7)
Remark 4.1
-
(a)
Boundedness of f and
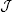 can be replaced by more general conditions, for example, growth or sign ones, if the method of a priori estimates is used. See, e.g., [16, 17].
can be replaced by more general conditions, for example, growth or sign ones, if the method of a priori estimates is used. See, e.g., [16, 17]. -
(b)
Continuity of v on is necessary for the construction of a continuous operator in Section 6. Note that then we need in Example 3.7.
-
(c)
Clearly, if f is continuous on , then f fulfils (4.7).
-
(d)
Let there exist , and , , such that
for a.e. and all . Then f fulfils (4.7). An example of such a function f is
where , , , .
5 Transversality
Consider , and define a set ℬ by
The following two lemmas for functions from ℬ are the modifications of lemmas in [10] and provide the transversality (cf. Remark 2.3) which will be essential for operator constructions in Section 6.
Lemma 5.1 Let γ satisfy (2.4), (4.3) and (4.5). Then, for each , there exists a unique such that
In addition .
Proof Let us take an arbitrary and denote
Then, by (2.4) and (5.1), we see that and
Since , condition (4.3) gives
Consequently, there exists at least one zero of σ in . Let be a zero of σ. By virtue of (4.5) and (5.1), we get, for , ,
That is,
Hence τ is a unique zero of σ, and (4.3) yields . □
Due to Lemma 5.1, we can define a functional by
where τ fulfils (5.2).
Lemma 5.2 Let γ satisfy (2.4), (4.3) and (4.5). Then the functional  is continuous.
is continuous.
Proof Let us choose a sequence which is convergent in . Then
and there exists such that
So, by virtue of (1.5) and (5.5),
We see that . For , define
By Lemma 5.1,
We need to prove that
Conditions (2.4), (1.5) and (5.6) yield
Let us take an arbitrary . By (5.3) and (5.9) we can find , and such that , for each . By Lemma 5.1 and the continuity of , we see that for , and (5.8) follows. □
6 Fixed point problem
In this section we assume that
and we construct a fixed point problem whose solvability leads to a solution of problem (2.1)-(2.3). To this aim, having the set ℬ from (5.1), we define a set Ω by
and for , we define a function as follows. We set, for a.e. ,
where  is defined by (5.4) and the point is uniquely determined due to Lemma 5.1. By (4.1)
is defined by (5.4) and the point is uniquely determined due to Lemma 5.1. By (4.1)
Now, we can define an operator by , where


Here the functionals and are defined such that the functions and are continuous at the point . Therefore
Differentiating (6.5) and using (3.6) and (6.3), we get
This together with (4.1) yields
Since (cf. (4.4)), we see that (6.4)-(6.6), (3.6), (4.1) and (4.2) give
Due to (6.8)-(6.10), we see that , , and the operator ℱ is defined well.
Lemma 6.1 Assume that (6.1) holds and that Ω and ℱ are given by (6.2) and (6.5), (6.6), respectively. Then the operator ℱ is compact on .
Proof Step 1. We show that ℱ is continuous on . Choose a sequence
which is convergent in , that is, (cf. (1.5)) there exists such that
Lemma 5.1 and Lemma 5.2 yield
where  is defined by (5.4). Denote
is defined by (5.4). Denote
We will prove that
By (4.7), (6.8), (6.11) and (6.13),
Using (4.1), we get
Since
the Lebesgue dominated convergence theorem and (6.16) give
Using (6.13) and (6.5), we get
The continuity and boundedness of  ,
, 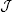 and v (cf. Lemma 5.2, (2.4), (4.2), (4.4) and (6.12)) imply
and v (cf. Lemma 5.2, (2.4), (4.2), (4.4) and (6.12)) imply
wherefrom, by the boundedness of G and (6.17),
Using (6.13) and integrating (6.8), we get
and, due to (6.15) and (6.18), we arrive at
Similarly, we derive
Properties (6.15), (6.19) and (6.20) yield (6.14).
Step 2. We show that the set is relatively compact in . Choose an arbitrary sequence
We need to prove that there exists a convergent subsequence. Clearly, there exists such that
Choose . By (5.1) and (6.2), it holds
for , . Therefore, the Arzelà-Ascoli theorem yields that there exists a subsequence
which converges in . Consequently, for each , there exists such that for each ,
Similarly as in Step 1, we prove (cf. (6.15), (6.19), (6.20))
which gives by (1.5) that is convergent in . □
Remark 6.2 If there exists such that for , then problem (2.1)-(2.3) has an impulse at fixed time and a standard operator , acting on the space of piece-wise continuous functions on and having the form
can be used instead of the operator ℱ from (6.5), (6.6). But this is not possible if γ is not constant on . The reason is that then an impulse is realized at a state-dependent point , and with τ instead of should be investigated on the space . But if we write a state-dependent τ instead of a fixed in (6.21), loses its continuity on , which we show in the next example.
Example 6.3 Let , and ℓ be from (2.5) with , and . Consider the functions
Clearly, uniformly on and hence
For , denote and . Assume that the barrier γ is given by the linear function on ℝ and the impulse function for , . Then
and, according to (6.21), we have for
Consequently,
due to (3.6). Hence and we have also , and is not continuous on .
Lemma 6.1 results in the following theorem.
Theorem 6.4 Assume that (6.1) holds and that the set Ω is given by (6.2), where
Further, let the operator ℱ be given by (6.5), (6.6). Then ℱ has a fixed point in .
Proof By Lemma 6.1, ℱ is compact on . Due to (5.1), (6.2), (6.5), (6.6), (6.10) and (6.22),
Therefore, the Schauder fixed point theorem yields a fixed point of ℱ in . □
7 Main result
The main result, which is contained in Theorem 7.1, guarantees the solvability of problem (2.1)-(2.3) provided the data functions f, 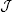 and γ are bounded (cf. (4.1)-(4.3)). As it is mentioned in Remark 4.1, Theorem 7.1 serves as an existence principle which, in combination with the method of a priori estimates, can lead to more general existence results for unbounded f and
and γ are bounded (cf. (4.1)-(4.3)). As it is mentioned in Remark 4.1, Theorem 7.1 serves as an existence principle which, in combination with the method of a priori estimates, can lead to more general existence results for unbounded f and 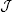 and concrete boundary conditions.
and concrete boundary conditions.
Theorem 7.1 Assume that (6.1) and (6.22) hold. Then there exists a solution z of problem (2.1)-(2.3) such that
Proof By Theorem 6.4, there exists which is a fixed point of the operator ℱ defined in (6.5) and (6.6). This means that


where G,  , , , are given by (3.6), (5.4), (6.3), (6.7), respectively. Recall that is a unique point in satisfying
, , , are given by (3.6), (5.4), (6.3), (6.7), respectively. Recall that is a unique point in satisfying
For , define a function z by
Differentiating (7.2), (7.3) and using (3.6) and (6.3), we get for a.e. , , and consequently
By virtue of (7.2)-(7.5), we have
Let us show that is a unique solution of the equation
in . According to (7.4) and (7.5), it suffices to prove
Since , we have (cf. (5.1) and (6.2))
Assume that the first condition in (4.6) is fulfilled. Then , for . Put
By (7.6), , and since γ is non-increasing, we have
due to (7.4). Using (4.5), we derive for
So, (7.8) is valid. If the second condition in (4.6) is fulfilled, we use the dual arguments.
Finally, let us check that . By (7.2)-(7.6) and (3.6), we have
Put
Then, according to (iii) of Definition 3.3 and Remark 3.2, we get . Further, using (3.7) from Lemma 3.5, we arrive at . Consequently, due to (2.5), (7.9) and (7.10), results in
□
References
Bainov D, Simeonov P: Impulsive Differential Equations: Periodic Solutions and Applications. Longman, Harlow; 1993.
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations. World Scientific, Singapore; 1989.
Samoilenko AM, Perestyuk NA: Impulsive Differential Equations. World Scientific, Singapore; 1995.
Bajo I, Liz E: Periodic boundary value problem for first order differential equations with impulses at variable times. J. Math. Anal. Appl. 1996, 204: 65-73. 10.1006/jmaa.1996.0424
Belley J, Virgilio M: Periodic Duffing delay equations with state dependent impulses. J. Math. Anal. Appl. 2005, 306: 646-662. 10.1016/j.jmaa.2004.10.023
Belley J, Virgilio M: Periodic Liénard-type delay equations with state-dependent impulses. Nonlinear Anal. TMA 2006, 64: 568-589. 10.1016/j.na.2005.06.025
Frigon M, O’Regan D: First order impulsive initial and periodic problems with variable moments. J. Math. Anal. Appl. 1999, 233: 730-739. 10.1006/jmaa.1999.6336
Benchohra M, Graef JR, Ntouyas SK, Ouahab A: Upper and lower solutions method for impulsive differential inclusions with nonlinear boundary conditions and variable times. Dyn. Contin. Discrete Impuls. Syst., Ser. A, Math. Anal. 2005, 12: 383-396.
Frigon M, O’Regan D: Second order Sturm-Liouville BVP’s with impulses at variable times. Dyn. Contin. Discrete Impuls. Syst., Ser. A, Math. Anal. 2001, 8: 149-159.
Rachůnková I, Tomeček J: A new approach to BVPs with state-dependent impulses. Bound. Value Probl. 2013., 2013: Article ID 22
Rachůnková, I, Tomeček, J: Second order BVPs with state-dependent impulses via lower and upper functions. Cent. Eur. J. Math. (to appear)
Rachůnková, I, Tomeček, J: Existence principle for BVPs with state-dependent impulses. Topol. Methods Nonlinear Anal. (submitted)
Tvrdý M: Linear integral equations in the space of regulated functions. Math. Bohem. 1998, 123: 177-212.
Tvrdý M: Regulated functions and the Perron-Stieltjes integral. Čas. Pěst. Mat. 1989, 114: 187-209.
Schwabik Š, Tvrdý M, Vejvoda O: Differential and Integral Equations. Academia, Prague; 1979.
Rachůnková I, Tomeček J: Singular Dirichlet problem for ordinary differential equation with impulses. Nonlinear Anal. TMA 2006, 65: 210-229. 10.1016/j.na.2005.09.016
Rachůnková I, Tomeček J: Impulsive BVPs with nonlinear boundary conditions for the second order differential equations without growth restrictions. J. Math. Anal. Appl. 2004, 292: 525-539. 10.1016/j.jmaa.2003.12.023
Acknowledgements
This research was supported by the grant Matematické modely, PrF_2013_013. The authors thank the referees for suggestions which improved the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
Both authors contributed equally to the manuscript and read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rachůnek, L., Rachůnková, I. First-order nonlinear differential equations with state-dependent impulses. Bound Value Probl 2013, 195 (2013). https://doi.org/10.1186/1687-2770-2013-195
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2013-195