- Research
- Open access
- Published:
The Cauchy problem for the modified Novikov equation
Boundary Value Problems volume 2014, Article number: 171 (2014)
Abstract
In this paper, we are concerned with the Cauchy problem for the modified Novikov equation. By using the transport equation theory and Littlewood-Paley decomposition as well as nonhomogeneous Besov spaces, we prove that the Cauchy problem for the modified Novikov equation is locally well posed in the Besov space with and and show that the Cauchy problem for the modified Novikov equation is locally well posed in the Besov space with the aid of Osgood lemma.
MSC: 35G25, 35L05, 35R25.
1 Introduction
Recently, Zhao and Zhou [1] considered the exact traveling wave solution to the following modified Novikov equation:
We recall that the Novikov equation
was discovered by Vladimir Novikov [2] and it possesses the bi-Hamiltonian structure, infinite conservation laws. The well-posedness and blow-up of the Cauchy problem for the Novikov equation in Sobolev spaces and Besov spaces have been investigated by some authors [3]–[7]. The weak solution of the Cauchy problem for the Novikov equation has been investigated by some authors [4], [5], [8]. Recently, Li and Yan [9] considered the Cauchy problem for the KdV equation with higher dispersion.
We define and . By using the fact that and for all and , we can rewrite (1.1) as follows:
Now we consider the following problem:
To the best of our knowledge, the well-posedness and blow-up of the Cauchy problem for (1.3) and (1.4) in Besov spaces are open up to now. More precisely, in this paper, motivated by [10], [11], using Littlewood-Paley decomposition and nonhomogeneous Besov spaces, we prove that the Cauchy problem for (1.4) is locally well posed in the Besov space with and we give a blow-up criterion.
To introduce the main results, we define
The main results of this paper are as follows.
Theorem 1.1
Letandand. Then there exists a timesuch that problem (1.3) and (1.4) has a unique solutionin. The mapis continuous from a neighborhood ofinintofor every. When, the solution to problem (1.3) and (1.4) is continuous in.
Theorem 1.2
When, (1.3) and (1.4) is locally well posed in the sense of Hadamard.
The remainder of this paper is organized as follows. In Section 2, we give some preliminaries. In Section 3, we establish local well-posedness of the Cauchy problem for the generalized Camassa-Holm equation in Besov spaces. In Section 4, we prove Theorem 1.2.
2 Preliminaries
In this section, the nonhomogeneous Besov spaces and the theory of transport equation which can be seen in [10]–[13] are presented.
Lemma 2.1
(Littlewood-Paley decomposition)
There exists a couple of smooth radial functionsvalued insuch thatis supported in the ballandis supported in the ring. Moreover,

and
Then, for, the nonhomogeneous dyadic blocks are defined as follows:
Thus.
Remark
The low frequency cut-off is defined by
It is easily checked that
as well as
with the aid of Young’s inequality, where is a positive constant independent of .
Definition
(Besov spaces)
Let , . The nonhomogeneous Besov space is defined by
In particular, . Let , and . Define .
Lemma 2.2
Let, , , then:
-
(1)
Topological properties: is a Banach space which is continuously embedded in .
-
(2)
Density: is dense in .
-
(3)
Embedding: if and .
-
(4)
Algebraic properties: , is a Banach algebra. is a Banach algebra ⇔ ⇔ or ( and ). In particular, is continuously embedded in and is a Banach algebra.
-
(5)
1-D Moser-type estimates:
-
(i)
For ,
-
(ii)
( if ) and , we have
-
(6)
Complex interpolation:
-
(7)
Real interpolation: , , , there exists a constant such that
In particular, for any, we have that
-
(8)
Fatou lemma: if
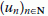 is bounded in and in , then and
is bounded in and in , then and
-
(9)
Let and be an -multiplier (i.e., is smooth and satisfies that , ∋ a constant , s.t. for all ). Then the operator is continuous from to . Notice that is continuous from to and is continuous from to .
-
(10)
The usual product is continuous from to .
-
(11)
There exists a constant such that the following interpolation inequality holds:
Lemma 2.3
(A priori estimates in Besov spaces)
Letand. Assume that, andbelongs toifor tootherwise. Ifsolves the following 1-D linear transport equation:
then there exists a constantdepending only on, , such that the following statements hold:
-
(1)
If or , then
or hence,
withifandelse.
-
(2)
If , and and , then
with
-
(3)
If , then for all , (1) holds true when .
-
(4)
If , then . If , then for all .
Lemma 2.4
(Existence and uniqueness)
Let, , , andbe as in the statement of Lemma 2.3. Assume thatfor someandandiforandandif. Then problem (2.2) and (2.3) has a unique solutionand the inequalities of Lemma 2.3can hold true. Moreover, if, then.
3 Proof of Theorem 1.1
By using the following six steps, we will complete the proof of Theorem 1.1.
First step: Approximate solution. We will construct a solution with the aid of a standard iterative process. Starting from , by the inductive method and solving the following linear transport equation (3.1) and (3.2), we derive a sequence of smooth functions 
It is easily checked that , by using Lemma 2.4 and the inductive method, for all , we have that (3.1) and (3.2) has a global solution which belongs to .
Second step: Uniform bounds. We will prove
for all .
Combining (2.4) of Lemma 2.3 with (3.1), we have
where
When , by using (4) in Lemma 2.2, we have
Combining (3.6)-(3.7) with (3.4), we have (3.3).
Let satisfy
By using (3.9), we have
When in (3.10), we have
By using (3.10) and (3.9), we have
With the aid of the mean value theorem, we have
where
Combining (3.13) with (3.12), we have that
Inserting (3.10)-(3.14) into (3.3) leads to
Consequently, is uniformly bounded in . By using the fact that with is an algebra and as well as the definition of the Besov spaces , we derive that
Since , which leads to that is an algebra, by using the -multiplier property of and the -multiplier property of as well as (3.8), we have
Consequently, combining (3.1) with (3.16) and (3.17), we derive that
which yields .
Third step: Convergence. We will derive that is a Cauchy sequence in .
For , from (3.1), we have
where
When , by using the multiplier property of , the multiplier property of and , we have
where , . Since , we have
By using (3.20), we have
When , from Lemma 2.4 and (3.20), we have
where
if and
if . From (3.23), if , by using with , we have
From (3.25), if , we have
It is easily showed that
Inserting (3.25)-(3.27) into (3.22), we have
We define
Combining (3.28) with (3.29)-(3.30), we have that
From (3.31) and (3.32), by using the Fatou lemma, we have that
Applying the Gronwall inequality to (3.33), we have that
From (3.31), we have that . Thus, . Consequently, is a Cauchy sequence in ; moreover, is convergent to some limit function .
When , by using (6) of Lemma 2.2, we derive that
where
Consequently, is a Cauchy sequence in and converges to some limit function .
Fourth step: Existence of solution in. Existence of solution can be proved similarly to [11].
Fifth step: Uniqueness of solution. We consider case and case , respectively. In fact, this can be proved similarly to [14].
Sixth step: Continuity with respect to the initial data. Continuity with respect to the initial data can be proved similarly to [6].
4 Proof of Theorem 1.2
Since and are Banach algebras, by using a proof similar to (3.3), we can prove that
for all  . We assume that
. We assume that
By a proof similar to (3.15), we can prove that
Thus, is uniformly bounded in . From (3.1), by using (4) in Lemma 2.2, we can prove that is uniformly bounded with respect to in .
Consequently, .
We define

By a proof similar to [15], we derive that
and with the aid of (2.1), we can prove that is a Cauchy sequence in .
The rest of Theorem 1.2 can be proved similarly to [13], [15].
References
Zhao L, Zhou SG: Symbolic analysis and exact travelling wave solution to a new modified Novikov equation. Appl. Math. Comput. 2010, 217: 590-598. 10.1016/j.amc.2010.05.093
Novikov VS: Generalizations of the Camassa-Holm equation. J. Phys. A 2009., 42: 10.1088/1751-8113/42/34/342002
Ni L, Zhou Y: Well-posedness and persistence properties for the Novikov equation. J. Differ. Equ. 2011, 250: 3002-3021. 10.1016/j.jde.2011.01.030
Wu XL, Yin ZY: Global weak solutions for the Novikov equation. J. Phys. A, Math. Theor. 2011., 44: 10.1088/1751-8113/44/5/055202
Wu XL, Yin ZY: A note on the Cauchy problem for the Novikov equation. Appl. Anal. 2013, 92: 1116-1137. 10.1080/00036811.2011.649735
Yan W, Li YS, Zhang YM: The Cauchy problem for the integrable Novikov equation. J. Differ. Equ. 2012, 253: 298-318. 10.1016/j.jde.2012.03.015
Yan W, Li YS, Zhang YM: The Cauchy problem for the Novikov equation. Nonlinear Differ. Equ. Appl. 2013, 20: 1157-1169. 10.1007/s00030-012-0202-1
Lai SY: Global weak solutions to the Novikov equation. J. Funct. Anal. 2013, 265: 520-544. 10.1016/j.jfa.2013.05.022
Li Y, Yan W: Well-posedness and ill-posedness of KdV equation with higher dispersion. J. Math. Anal. Appl. 2014, 416: 647-658. 10.1016/j.jmaa.2014.01.035
Danchin R: A few remarks on the Camassa-Holm equation. Differ. Integral Equ. 2001, 14: 953-988.
Danchin R: Fourier Analysis Method for PDEs. 2005.
Chemin JY: Localization in Fourier space and Navier-Stokes. In Phase Space Analysis of Partial Differential Equations. Scuola Norm. Sup., Pisa; 2004:53-136.
Danchin R: A note on well-posedness for Camassa-Holm equation. J. Differ. Equ. 2003, 192: 429-444. 10.1016/S0022-0396(03)00096-2
Yan W, Li YS, Zhang YM: The Cauchy problem for the generalized Camassa-Holm equation. Appl. Anal. 2014, 93: 1358-1381. 10.1080/00036811.2013.833325
Yan W, Li YS, Zhang YM: The Cauchy problem for the generalized Camassa-Holm equation in Besov space. J. Differ. Equ. 2014, 256: 2876-2901. 10.1016/j.jde.2014.01.023
Acknowledgements
We would like to thank the reviewers for careful reading and valuable comments on the original draft.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
We declare that we have no competing interests.
Authors’ contributions
All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hou, X., Zheng, Y. The Cauchy problem for the modified Novikov equation. Bound Value Probl 2014, 171 (2014). https://doi.org/10.1186/s13661-014-0171-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-014-0171-x
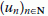 is bounded in and in , then and
is bounded in and in , then and